Отражение и преломление В.э. На границе двух диэлектриков или диэлехс-трика и полупроводника падающая В. э.частью отражается, частью преломляется. Законы отражения и преломления В.э. совпадают с оптическими законами отражения и преломления поляризованной волны, в плоскости поляризации к-рой лежит магнитный вектор. Законы эти получаются из уравнений Максвела и вытекающих из них, без каких-либо добавочных гипотез, пограничных условий. Условия эти следующие: на границе раздела тангеьщиальные (индекс t) составляющие электрического, и магнитного напряжения не изменяются, т. е.

Ьд = ,.3 и Щ = Я ,; (19)

нормальные же составляющие (индекс п) удовлетворяют условиям:

f7£ ,i = iji;,2 и tiH,x = i А.2. (20)

где 6 обозначает комплексный диэлектрич. коэфф., а значки i и а показьшают к какой среде относятся соответствующие величины. При отражении амплитуда электрич. вектора меняет знак (происходит потеря полуволны), а магнитного-знак сохраняет. При нормальном падении амплитуды электрическ. и магнитного векторов в падающей (индекс о) и в отраженной (индес г) волне связаны соотношением:

(21)

Так как энергия пропорциональна квадрату амплитуды, то коэффициент отражения, определенный как отношение отраженной и падающей энергии для нормального падения, равен:

В формулах (21) и (22) р обозначает вообще комплексный относительный показатель преломления двух сред, на границе которых происходит отражение. Для границы диэлектрик-металл, для которого выполняется уравнение (18):

R=l- (22)

Величина R, приведенная в ур-ии (22), весьма близка к 1; т. о. поверхность металла является почти идеальным зеркалом для В.э.

Стоячие В. э. Когда на плоскую металлическую поверхность нормально падает и отражается плоская В. э., то в пространстве перед зеркалом распространяются в прямо противоположные стороны две В. э. практически равных амплитуд. Наложение двух таких волн дает систему стоячих волн. Согласно предыдущему, имеем: в падающей волне

E,E/<i-, в отраженной волне

Аа р + 1

Сложив эти выражения и взяв действительную часть суммы, получаем для стоячей волны:

(23)

= -2Ео sin 271 * sin 2л

Для напряжения магнитного поля в стоячей волне получается аналогично:

Я, = 2Яо cos 27t у cos 27t . (23)

Выражения эти показьшают, что в стоячей В. э. между электрич. и магнитным векторами существует сдвиг фаз в четверть периода во времени и в четверть волны в пространстве. Т. о. пучности электрич. напряжения совпадают с узлами магнитного, и наоборот. В частности, на поверхности отражающего зеркала лежит узел электрического и пучность магнитного напрялсений. В.э.,испускаемые электрическ. вибраторами (см. Диполь электрический), находящимися в однородной изотропной среде, па достаточном расстоянии от вибратора (см. Волновая зона) представляют собою сферич. В. э., в центре к-рых находится излучающий вибратор (фиг. 3). С увеличением радиуса

сферы, амплитуды электрического и магнитного полей таких волн убывают, как показал Герц, обратно пропорционально рас-, стоянию от вибратора. В остальном свойства сферических В.э. аналогичны указанным выше свойствам волн плоских. В пределах небольшого телесного угла (6) часть сферической волны можно считать плоской.

Распространение В. э. вдоль поверхности земли является для радиотехники вопросом первостепенной важности. Эта задача полностью до сих пор не разрешена в виду того, что крайне трудно учесть влияние всех факторов. Решение этой проблемы д;1я частного случая [пренебрегая кривизной земной поверхности и в предположении, что земная поверхность является идеальным проводником (ff=cx))] дал М. Абрагам. Результат, к к-рому приводит теория, для этого случая следующий: В. э., распространяющиеся от излучающего вибратора (антенны) в воздухе, совпадают с волнами, которые получились бы в отсутствии земли при условии, что, кроме реально существующего вибратора (антенны), излучает и его зеркальное изображение в поверхности земли. Все поле эл.-м. волн получается при этом симметричным относительно плоскости раздела (воздух-земля). Электрич. силы повсюду перпендикулярны к этой плоскости, магнитные-ей параллельны. Разумеется, реально существует только половина этого поля, распространяющаяся над плоскостью раздела-в воздухе.

Полное решение той же задачи для второго частного случая-почвы конечной проводимости-дано Зоммерфельдом. Главнейшие результаты этой математически весьма сложной теории следующие. От излучающего вибратора распространяются волны двух типов: в первой среде (воздух) и

во второй (почва) распространяются независимо две пространственные волны. Кроме того, вдоль поверхности раздела распространяется третья, поверхностная волна, амплитуды полей которой убывают обратно пропорционально корню квадратному из расстояния. Кроме того, вследствие поглощения энергии проводящей средой, амплитуды полей всех трех волн убывают по показательному закону. Затухание это-наибольшее для пространственной волны, распространяющейся в почве, и наименьшее для пространственной волны в воздухе. При не слишком больших затуханиях поверхностная волна на значительном протяже-Ш1И вокруг вибратора (антенны) преобладает над волной пространственной. Однако, так как показательная функция убывает быстрее любой степенной, то, начиная с некоторого расстояния от антенны, начинает преобладать волна пространственная, распространяющаяся в воздухе. Вблизи поверхности земли электрическ. поле наклонено в сторону распространения В. э. Амплитуды вертикальной и горизонтальной составляющих этого поля связаны соотношением:

(2-i)

где Eg и Е - амплитуды вертикальной и горизонтальной составляющих в воздухе, £2-комплексный диэлектрич. коэфф. почвы, %-диэлектрич. коэфф. воздуха. Соотношение это показывает, что вышеуказанные составляющие сдвинуты во времени по фазе. В результате этого вблизи поверхности земли йолучается вращающееся (эллиптическое) электрическ. поле. Горизонтальная составляющая электрическ. поля (фиг. 4)

Фиг. 4.

указывает на существование составляющей вектора Пойнтинга (на фиг. стрелка с), направленной вертикально вниз и характеризующей поглощение энергии электромагнитных волн почвой. к. Теодорчин.

П р а к т и ч е с к. ф - л ы. В приведенных выше двух частных случаях решения сложнейшей задачи радиотехники-распространения В. э. в условиях реальной обстановки-учтено слишком незначительное количество факторов, чтобы выведенные ф-лы могли соответствовать действительности. На самом деле в процессе распространения В. э. доминирующую роль играют еще следующие факторы: ионизация всякого рода, имеющаяся в атмосфере, существование на высоте 40-100 км так называемого слоя Хивисайда, земной магнетизм, солнечные пятна и др. Работы многих ученых (за последние годы Шулейкина, Мейснера, Эккерслея, Хоу, Остина и др.) до сих пор не привели к формуле,

количественно учитывающей все причины, влияющие на распространение В. э. всех длин. Подробный синтез решений по этому вопросу-см. Электромагнитные волны и Волны короткие. Ныне для практических целей расчета радиосвязи употребительны следующие две формулы: 1) Остина:

o.ooud

где I-сила тока в антенне передающей радиостанции в А, h-действующая высота той же антенны, d-расстояние до приемной радиостанции, Я-длина волны радиопередачи (все длины-в км), Е-напряженность электрич. поля в fiY/M; формула действительна для условий передачи на волнах Я>300л*, днем, летом, по водной поверхности. 2) Эккерслея:

где Е, I, h, X я d-то же, что и выше, а

f?o=-j (Я-высота слоя Хивисайда, часто

принимаемая 40 км); а = 0,0011-0,0022 (обычно принимают а =0,0016). Зная Е, легко получаем Н по формуле: Е~сН, где Е и Н выражены в электромагнитной системе единиц. Измерения величины Е показывают резкие колебания ее в зависимости, главн. обр., от освещенности пространства, отделяющего приемную радиостанцию от передающей. Однако средние годовые значения измеряемого Е часто хорошо согласуются с результатами по ф-ле Остина. Факторы, влияющие на распространение В. э. в условиях реальной обстановки, проявляются не только в виде колебаний силы поля по абсолютной величине (вектор JE), но и в виде изменения направления фронта волны (вектора Л, а следовательно, и вектора Пойнтинга). Колебания силы поля, зависящие от многих причин, имеют пока две твердо установленные периодичности: а) сезонное изменение напряженности, характеризуемое, напр., на фиг. 5 графиком приема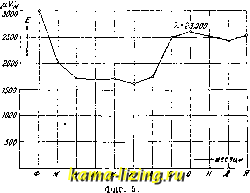

радиостанции Лафайет (Бордо) на расстоянии 460 7ш; б) суточное изменение той же величины, характеризуемое, напр., графиком приема в Москве (Всесоюзным электротехническим ин-том) одной из радиостанций

С. Ш. А. (фиг. 6). Об изменении направления фронта волны и практич. последствиях этого см. Пеленгаторы. Вопрос распространения В. э. в целом решается учеными различных государств, при чем их работа координируется в I секции ( Распространение электромагнитных волн ) Международного

£<alfi, wss

7.-/SI20M

2 3 5 6 Р 8 9 Ю II 12 15 И-15 16 I? 18 19 2021 222324 1 2 Нью-Йоркское время

Фиг. 6.

союза по научному радио (U. R. S. I.), председателем которой состоит Л. В. Остин. Детали современного состояния закона радиопередачи освещены в последнем отчете Остина, напечатанном в Proceedings of the Institute of Radio Engineers ,N. Y., 1928, vol. 16,3. Полная библиография по вопросу распространения В.э. имеется в Kinire А. Sacklow-ski, Die Ausbreitung d. elektromagnetischen Wellen, В., 1928.

Лит.: Хвольсон О. Д., Курс физики, т. 5, Берлин, 1923; ЭйхенвальдА. А., Теоретич. физика, ч. I-Теория поля, М.-Л., 1926;Enzyklopadie d. mathematischen Wissenschaften, В. 5, Abt. 3, Н. I, p. 95, Lpz., 1909; С о h n E., Das elektromagnetische Feld, Berlin, 1927; Abraham M., Theorie der Elektrizitat, B. 1, 6 Aiifl., §§ 68-80, Leipzig, 1921; Ollendorff F., Die Grundlagen d. Hochfrequenz-technik, p. 479, Berlin, 1926; M i s e s R. u. Frank P., Die Differential- u. Integralgleichungen d. Mecha-nik und Physik (Zugleich Riemann - Weber, Die partiellen Differentialgleichungen der mathematischen Physik), Brschw.. 19 27; Sommerfeld A., Ausbreitung der Wellen in der drahtlosen Telegraphie, Ann. d. Phys.o, Leipzig, 1909, B. 28, p. 665; R ii d en-berg R., Aussendung und Empfang elektrischer Wellen, Berlin, 1926. B. Баженов.

ВОЛОКНА м. б. растительного или животного происхождения.

Растительные волокна делятся на две группы: волоски (Trichomae) и лубовые (склеренхимные) В. Волоски вырастают

из эпидермиса семени, окружая его со всех сторон (напр. Gossypium-фиг. 1) или образуя хохолок (например As-clepias-фиг. 2, Са-lotropis, Strophan-thus-фиг. 3). Иногда волоски принадлежат кожице плода (напр. Вош-Ьах). Очень редко утилизируются во-1 лесистые покровы

листьев (например Cibotium) или плодовые волоски (например Typha). Волоски обыкновенно одноклеточ-

ны (Gossypium, Asclepias и другие), реже они состоят из одного (Cibotium) или нескольких (Eriophorum) рядов клеток. Длина и толщина волосков сильно колеблются (табл. 1).

Табл. 1.-П редельные размеры волосков растений.

Клеточные стенки волосков, Покрытые снаружи кутикулой, а внутри очень тонким слоем высохшей протоплазмы, имеют в середине полость, заполненную воздухом. Волоски различных растений отличаются формой поперечного среза. В серной к-те кутикула и протоплазма волосков нерастворимы.

Волокна лубовые представляют собою части сосудистых пучков,расположенных в стеблях двудольных растений (например Linum, Cannabis, Corchorus и др.) или в листьях однодольных (Aloe perfoliata. Agave si-salana, Musa texti-lis, Phormium tenax и др.), реже-в стеблях однодольных растений или плодов (напр. мочало,получаемое из растений Luff а cylindrica и L. acutangula).

Фиг. 2.

Фиг. 3.

Иногда В. состоят из целых сосудистых пучков (Cocos nucifera) или даже из целой группы их (фиг. 4). Сосудистые пучки в виде тяжей пронизывают листья, стебли и корни