Графическое определение перемещений. Графическ. способам отдают предпочтение, когда требуется определить перемещения целого ряда точек, напр., прогибы всех узлов фермы. В отдельных случаях и для нахождения перемещения одной точки графические приемы могут дать наиболее простое, а иногда и единственное решение, именно, когда аналитич. решение сопряжено с интегрированием сложно интегрируемых или неинтегрируемьЕх ф-ий. Г. о. п. применяется как для систем сплошных (балки, арки, рамы), так и для систем шарнирно-стержневых (фермы). И в том и в другом случае предполагается, как это вообще принято в теории сооружений, что перемещения являются величинами весьма малыми по сравнению с общими размерами тела; поэтому для тел гибких (проволока, кабель и т. п.) излагаемые ниже приемы неприменимы.

Построение перемещений в сплошных системах. В сплошных системах пренебрегают влиянием продольной и поперечной силы на деформации и строят перемещения, учитывая только изгибающий момент. Из теории известно выражение кривизны изгиба: = - где М-

изгибающий момент в сечении, Е-модуль упругости первого рода, I-момент инерции.

сечения и q-радиус кривизны, для которого дифференциальная геометрия дает ур-ие:

1 у .

е [1 + (y)J* Пренебрегая в знаменателе величиной {уУ в виду ее малости по сравнению с единицей, получаем дифференциальное выражение упругой линии в следующем виде:

У EI

Из сопоставления этого ур-ия с ур-ием веревочной кривой (см. Веревочный многоугольник) Ну = -Z, где И-полюсное расстояние, у-ордината кривой и z-ордината эпюры распределений нагрузки, заключаем, что упругая линия может быть построена как веревочная кривая, при условии, что за нагрузку будет взята условная распределенная нагрузка = > а полюсное расстояние Н будет принято равным единице. Построение это вполне аналогично построению эпюры моментов от действительной нагрузки и производится след. образ. За нам

грузку принимают эпюру значений = и делят на возможно большее число частей. Площади каждой такой части, равные As,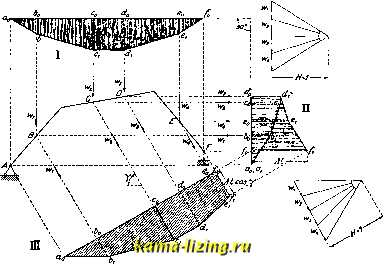

Фиг. I.

заменяют равными им по величине сосредоточенными силами W, приложенными в ц. т. этих площадей. Затем эти условные силы W о,шо,я! на ось бруса, направляют их параллельно искомым перемещениям и строят для них веревочную кривую при полюсном расстоянии, равном единице в масштабе силового многоугольника. Ординаты построенной таким образом упругой линии измеряются относительно некоторой замыкающей, способы построения к-рой видны из следующего примера (фиг. 1), в котором для бруса ломаного очертания построены перемещения в трех направлениях: перпендикулярно плоскости подвижности опоры (I), параллельно этой плоскости (II) и в косом напра-

влении (III). При построении перемещеьшй в направлении, перпендикулярном плоскости качения подвижной опоры, замыкающая определяется тем, что в упругой линии точки, соответствующие опорам, не имеют в искомом направлении перемещений, следовательно, замыкающей будет прямая, соединяющая точки, полученные путем снесения на веревочную кривую опор. При определении перемещений в направлении подвижности правой опоры, т. е. в направлении, перпендикулярном предыдущему, замыкающая определяется из условия, что перемещение неподвижной опоры А равно нулю, а поворот сечения бруса на этой опоре, т. е. угол наклона первого луча веревочного м-ка к замыкающей, равен углу поворота, определенному построением (I). Исходя из этих соображений, построение перемещений в этом направлении ведут след. образом: упругие грузы W направляют параллельно направлению подвижности правой опоры и строят для них веревочный мн-к, стороны которого проводятся в направлении, перпендикулярном соответствующим сторонам мн-ка (I). Затем через точку к-рая соответствует неподвижной опоре Л, проводят за-мьжающую под углом в 90° к замыкающей мн-ка в построении (I). Отрезки относительно этой замыкающей а-а-, bo-bi, Cq-o,.. . будут равны перемещениям точек А, В, С,..., а, отрезком М, = fo-fi определится величина перемещения подвижной опоры F. Для нахождения перемещений в косом направлении условные силы W ведут параллельно этому направлению и строят веревочный мн-к при том же полюсном расстоянии Н, как и в построениях (I) и (II). Положение же замыкающей определится тем, что в указанном направлении перемещение левой опоры равно нулю, а правой- проекции на это направление полной величины перемещения правой опоры, т. е. Мcosy.

Если для рассматриваемой системы момент инерции является величиной постоянной, то

величина условной нагрузки = j-g прямо

пропорциональна ординатам эпюры М. В этом случае за нагрузку можно принять площадь эпюры моментов, но так как упругие грузы в этом случае увеличатся в EI раз, то для получения перемещений по-прежнему в масштабе чертежа надо и полюсное расстояние взять соответственно увеличенным в EI раз.

Если сечение балки изменяется так(фиг.2), что в отдельных участках (1-м, 2-м, 3-ми т. д.) моменты инерции Ji, 1, I3 остаются постоянными, то за условную нагрузку целесообразно принять значения нагрузок,

равных Jo, lo, h, и т. д., а полюсное расстояние н взять равным I-EIq, где Jo-произвольно взятое значение момента инерции (на фиг. 2 принято Jo=Ji). В предыдущем изложении предполагалось, что перемещения д. б. построены в масштабе чертела, но т. к. перемещения - величины

Фиг. 2.

весьма малые, то практически их приходится строить в значительно увеличенном масштабе. Для чертежа, построенного в масштабе у натуральной величины и при требуемом увеличении перемещений в m раз против натуральной величины, общее увеличение перемещений против масштаба чертежа будет в тк раз, что достигается путем уменьшения во столько же раз полюсного расстояния, т. е., в том случае, когда за условную нагрузку принята эпюра моментов, полюсное расстояние Н принимается

равным 1-.

Изложенные приемы применимы и для построения перемещений в кривых стержнях (брусьях малой кривизны) в тех случаях, когда возможно пренебречь влиянием на деформации нормальной и поперечной сил (см. Арки). Пример такого построения горизонтальных и вертикальных перемещений для кривого бруса переменного сечения дан на фиг. 3. За упругие грузы в этом построении взяты величины My As, а полюсное расстояние Н принято равным 1 -Шо, где М-среднее значение момента в данном участке As, I - среднее значение момента инерции для этого участка и Jo-нек-рый произвольно выбранный момент инерции.

Построение перемещений в статически неопределимых системах. После того как найдены лишние неизвестные и построена эпюра моментов, построение перемещений в статически неопределимых системах не отличается от такового для систем статически определимых. Па фиг. 4 показано построение прогибов для неразрезной балки постоянного сечения, заделанной на левом конце и с консолью на правом. За условную нагрузку принята эпюра моментов, построенная при помощи фокусных то-

чек (см. Валки неразрезные); полюс выбран так, чтобы первый луч был горизонтальным; направление этого луча будет служить замыкающей, так как ось бруса в месте заделки остается горизонтальной. Построенная упругая линия пересечет эту замыкающую под всеми опорными точками.

Перемещения в фермах. Для нахождения перемещений в фермах выделяют из состава фермы непрерывный шарнирно-стержневой зигзаг, проходящий через опоры и через те узлы, перемещения которых требуется определить (фиг. 5). Образования прогибов в фермах отличаются от таковьсс в системах сплошных тем, что в последних каждому элементу ds оси изгибаемого бруса соответствует угловая деформация, равная

- ds. Эта угловая деформация принимается, при построении перемещений, за элементарный упругий груз W, а вся условная нагрузка в целом представляется в виде эпюры сплошной распределенной нагрузки м

В фермах же, согласно принятой схеме

расчета их как шарнирно-стержневых систем, изгибающий момент в стержнях равен нулю, стержни, составляющие ферму, остаются прямыми, и угловые деформации М имеются только в узлах системы. Следовательно, перемещения выделенного из состава фермы зигзага (фиг. 5) зависят от сосредоточенных угловых деформаций-углов в между его сторонами и от удлинений его сторон S. Перемещения, вызванные угло-вьпйи деформациями в узлах, на основании рассуждений, аналогичных сделанным по отношению к сплошньш системам, могут быть построены, как веревочный многоугольник для сосредоточенных упругих грузов Wjc, равных угловым деформациям Дб в узлах шарнирной цепи. Величины этих последних определяются из условия деформации всей фермы; способы определения их указаны ниже. Перемещения, получающиеся в зигзаге шарнирной цепи в результате удлинения ее сторон, м. б. также получены при помощи веревочного мн-ка путем выражения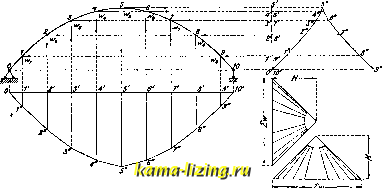

Фиг. 3.

их через упругие грузы W. Действительно, перемещения, вызываемые удлинением какого-нибудь стержня S]c на величину AS, могут быть представлены как сумма двух