давления можно пренебречь работой расширения воздуха и считать, что работа трения равняется работе давления, т. е.

Р1-Рг jR I т т d При скоростях движения воздуха вьнпе критической, что имеет место во всех случаях практики, движение потока воздуха будет вихревым. Критическая скорость воздуха зависит от t°, диаметра трубопровода и давления. В табл. 1 дается критическая скорость воздуха при темп-ре = 20°.

Табл. 1.-к р и т и ч е с к а я скорость воздуха при 20° в м/ск.

При вихревом движении И зависит от квадрата скорости потока воздуха и его уд. в. Считая 4 J2 = 10 0009 y гp будем иметь:

или, выражая потерю давления в м воздушного столба, получим основное уравнение для расчета В.:

где 10 000 = , или 10V = 510A.

от d, у, от внутреннего трения частиц воздуха, т. е. вязкости [i, мв большой степени от шероховатости внутренней поверхности трубопровода. Вводя значение дина-

мическ. вязкости v = > мы можем считать,

что X=f{w, d, v). Функциональная зависимость Я была определена Рейнольдсом (Reynolds) в форме:

=Г(-} (4)

отсюда следует, что для газа и жидкости, напр. для воздуха и воды, при различных значениях w, d, v коэфф-т Я будет одинаков в том случае, если параметр Рейнольд-

са - для воздуха будет равен парамет-

ДЛЯ воды. Определяя опытным путем

для отдельных сортов труб значения Я при различных значениях мы получим для каждого сорта трубы кривую изменения Я, при изменении - не зависящую от вещества протекающего по трубе потока, т. е. одного и того же значения как для капельных жидкостей, так и для газов. Это замечательное свойство параметра Рейнольдса дает возможность объединить в одно целое результаты всех опытных работ в области течения потока по трубопроводу независимо от того, с какой жидкостью или с каким газом производились исследования. Результаты этих исследований приведены на помещенной ниже диаграмме.

0.05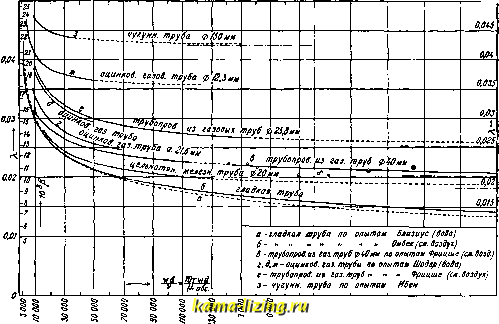

Ур-ие (3) дает зависимость между падением давления в трубопроводе h, его длиною I, диам. d и скоростью w потока воздуха. По диаметру и скорости легко определяется количество воздуха, протекающего в единицу времени. Входящий в уравнение (3) коэфф. Я не является постоянным, а зависит

Изменения Я протекают по закону гиперболы. Омбек дает следующее значение:

. 0,242

-

Для определения параметра Рейнольдса необходимо знать величину вязкости ju, зави-

сящей от Г. В физике вязкость (л выражается по абсолютной системе измерений; в данном случав надо вязкость выразить в технической системе. Легко определить, что fmexH.-

= ( обе., а следовательно, Гщехм. =

и ffl-w-d Значения абсолютной вязко-

iaбc.

Сти ДЛЯ воздуха даются в табл. 2.

ществить начальную скорость Wi, определяется по уравнению:

\ d Jmax )

- 2,303 1

где wl==g-k-pi-Vj и является квадратом начальной скорости распространения звука в воздтсе. При полученной длине lax ско-

Табл. 2.- Значения lOVoc. воздуха.

рость потока воздуха в конце трубопровода будет равна скорости звука. Давление в конце воздухопровода

Pmin

Рассмотрение диаграммы показывает, что для гладких труб (цельнотянутых калибрированных) при увеличении параметра

коэффициент Я неограниченно уменьшается. Для труб с шероховатой поверхностью сопротивление движению потока, вызываемое неровностями стенок труб, не может исчезнуть с увеличением ; поэтому для труб с шероховатой внутренней поверхностью с увеличением коэфф-т Я будет стремиться

к конечному пределу Л ; для шероховатых поверхностей кривые Я диаграммы имеют горизонтальные асимптоты (показанные на диаграмме пунктиром) на расстоянии Я от оси абсцисс. Из сказанного следует, что ур-ие Я для шероховатых труб будет иметь следующий вид:

(Я-Я )=. Const.

При расчете В. необходимо принимать во внимание потери давления при прохождении воздушного потока через вентили, отводы, угольники и компенсаторы; необходимо также учитывать изменения давления в местах соединения труб. Исследования Брабе (Brab-Ьёе) показали, что в этих случаях давления изменяются пропорционально квадрату скорости; это падение давления м. б. выражено высотой столба Ah - Для нормальных вентилей § = 6,5-7; для угольников =1,5-2; для отводов в 90°, при радиусе закругления r>bd, =0. Для расчета все местные сопротивления заменяются приведенной длиной I трубопровода, на основе соотношения:

d-2g

20

откуда приведенная длина r = --d. Полученные приведенные длины суммируются с геометрич. длиной В., и но полученной суммарной длине ведется расчет.

Для очень длинных В. предположение о незначительности работы расширения проходящего по трубопроводу воздуха будет неверно. Для этого случая, при адиабатическом процессе, максимальная длина воздухопровода, при которой еще возможно осу-

Если противодавление в конце В. будет больше Pmin то скорость Wi вообще не будет достигнута. Для расчетов В. длиной от Va ДО V* huix применяются обьганые расчетные уравнения (2), (3) и (4). Для В. длиной до Zoa, потеря давления м. б. весьма точно определена по уравнению:

й-р=а(1-/1-).

Лит.: Schule W., Technische Thermodynamik, в. 1, Berlin, 1 923; 0 m be к Н., Druckverlust str6-mender Luft in geraden zylindrischen Rolu-Ieitungen, Forschungsarbeiten , H. 158-159; В lasius H.,Da8 Ahnlichkeitsgesetz bei Reibungsvorgungen, Z. d. VDI , 1912, p. 639; Biel R., tfber d. Druckh6henverlu8t bei d. Fortleitungen tropfbarer u. gasfCrmiger Flvissig-keiten, eMitt. (iber Forsciiungsarbeiten , H. 44; В r a b -b 6 e. Die Berechnung verschiedener Rohrnetze auf einbeitl. Grundlage, Z. d. VDI , 1916; S с Ь u 1 e W., Tecbnische Tbermodynamik, B. 2, Abschnitt 52-t)ber die Berechnung sehr laager Erdgasleitung, В., 1923; H utte, Das Ingeuieurs Taschenbuch, B. 1, В., 1926.

ВОЗДУШНАЯ ПЕСОЧНИЦА, прибор, подводящий песок к рельсам впереди ведущих колес локомотива для увеличения трения между ними. Недостаток обыкновенных песочниц заключается в том, что высыпающийся на рельсы песок во время движения локомотива сдувается ветром. Для устранения этого заставляют песок двигаться по трубам не собственным весом, как это происходит в обыкновенной песочнице, а под действием сжатого воздуха (от тормозного компрессора). Воздушное сопло, располагаемое у песочного ящика, разрыхляет песок в ящике, засасывает в трубы и прогоняет его в распыленном виде по трубам к месту соприкасания колес с рельсами. Для успешной работы В. п. необходимо, чтобы песок был тщательно высушен и просеян. Существует

много раЗН. конструкций В. п. п. Краеовскнй.

ВОЗДУШНАЯ ПРОСЛОЙКА, один из видов изолирующих слоев, уменьшающих теплопроводность среды. В последнее время значение В. п. особенно возросло в связи с применением в строительном деле пустотелых материалов. В среде, разделенной В. п., тепло передается: 1) путем лучеиспу-схеания поверхностей, прилегающих к В. п., и путем теплоотдачи между поверхностью и воздухом и 2) путем переноса тепла воздухом, если он подвижен, или путем передачи тепла одними частицами воздуха другим вследствие теплопроводности его, если он неподвижен, при чем опыты Нуссельта доказывают, что более тонкие прослойки, в которых воздух может считаться почти

неподвижным, обладают меньшим коэфф-том теплопроводности к, чем более толстые прослойки, но с возникающими в них конвекционными течениями. Нуссельт дает следующее выражение для определения количества тепла, передаваемого в час В. п.:

8i 8, S /

где F-одна из поверхностей, ограничивающих В. п.; Яо-условный коэфф-т, числовые значершя которого, зависящие от ширины В. п. е, выраженной в м, даются в прилагаемой табличке:

Si и -коэфф-ты лучеиспускания обеих поверхностей В. п.; S-коэфф-т лучеиспускания абсолютно черного тела, равный 4,61; ©1 и 62-темп-ры поверхностей, ограничивающих В. п. Подставляя в формулу соответствующие значения, можно получить нужные для расчетов величины Тс (коэфф. теплопроводности) и -i (изолирующей способности) В. п. различ. толщины. С. Л. Прохоров составил по данным Нуссельта диаграммы (см. фиг.), показывающие изменение величин А; и

В. п. в зависимости от их толщины, при чем наивыгоднейшим участком является участок от 15 до 45 мм. Меньшие В. п. практически трудно осуществимы, а 66 ль-7i шие дают уже значительный коэффициент теплопроводности (около 0,07).

Следующая таблица дает величины h

для различных материалов, при чем для воздуха дано несколько значений этих величин в зависимости от толщины слоя.

Таблица значений коэффициентов h и l/ft для различных материалов.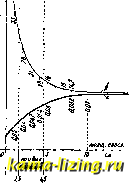

Т. о. видно, что часто бьшает выгоднее делать несколько более тонких В. п., чем применять те или другие изолирующие слои. В. п. толщиной до 15 мм может считаться изолятором с неподвижным слоем воздуха.

при толщине 15-45 мм-с почти неподвижным и, наконец, В. п. толщиной свыше 45- 50 мм должны признаваться прослойками с возникающими в них конвекционными течениями и потому подлежащими расчету на общем основании.

Лит.: Прохоров С. Л., Современное строительство из пустотелых бетонных камней с железобетон, каркасом, М., 1926; Чаплин В. М.,Курс отопления и вентиляции, вып. 1,М.,1924. С. Бекнев.

ВОЗДУШНАЯ СЕЛИТРА, см. Селитра.

ВОЗДУШНАЯ СУШКА, см. Сушка.

ВОЗДУШНОЕ ОБОГАЩЕНИЕ -один из спосооов разделения в струе воздуха руд или других полезных ископаемых на составляющие их минералы. Закон Риттингера, устанавливающий, что падение зерен в воде, с достаточной для практич. целей точностью, может быть принято происходящим по закону равномерного движения с постоянной скоростью, к В. о. не применим благодаря малой плотности воздуха и способности его сжиматься. Вообще говоря, разность скоростей падения зерен в воздухе ощутима лишь при условии уменьшения влияния ускорения силы тяжести; поэтому для разделения всегда применяют падение зерен в струе восходящей или горизонтальной, но не нисходящей. Вследствие затруднений при создании струи воздуха, способной .поднять крупные зерна руды, обработке подвергается лишь мелочь; В. о. неприменимо для очень мелких пылевидных частиц, легко уносимых струей воздуха. На тех же принципах основывается к л а с с и ф и к а ц и я по крупности для частиц одного и того же вещества и, кроме того, обеспыливание. В том или ином случае на минеральную частицу действует сила струи воздуха, которая может быть выражена след. ф-лой:

где Р-сила, действующая на частицу, в цг, г-опытный коэфф-т, зависящий от формы частицы (для плоской поверхности он изменяется в пределах от 1 до 3), v-скорость струи воздуха в мск, у-вес 1м воздуха в кг (у=1,293 кг/м), F -площадь сечения частицы, HopMa-ibnaH к направлению струи, в л**, д-ускорение силы тяжести.

Под влиянием силы тяжести частица оказывает сопоотивление: G=W-6, где 6г-вес частицы, W-объем ее, У-уд. вес. Вследствие этого частица будет поднята силой

R = ,p.y.F-~~W-d

(потерей в весе тела, равной весу вытесненного им воздуха, мы пренебрегаем вследствие ее ничтожной величины).

Если принять, что частица имеет форму шара, то

Для двух частиц одного и того же вещества та из них будет поднята струей воздуха выше, диаметр которой меньше; именно, если частица с диаметром будет поднята на высоту \, а частица d на высо-

Условие, при к-ром частицы двух разных минералов (диам. й и уд. вес 6 и диам. D и уд. вес d) будут подняты на одинаковую