Имеем: х-х\ = 24 ; = Г = 60 ; w =

= 0,4; и-1 = -0,6. Получаем:

lg sin 0=10= 3,46373 иАг/ = 0,01656

ц(ц-1) 1-2

Ар = 0,00043

lg sin 0°1024 = 3,48072 Приближенное решение у р-и й. Дано ур-ие f{x) = {). Вычисляя значения f{x) (напр. по таблицам), находим 2 таких значения Хх и Жз, что 2/1=Яж1) и УгКх имеют разные знаки. Это значит, что кривая y=f{x) пересекает ось х между Xi и х.

1-й способ. Чтобы приближенно найти точку пересечения, заменяем кривую прямой, соединяющей точки (xi, у) и (жа, 2/2) и ищем -абсциссу ее точки пересечения с осью X (ордината Уя=0). Имеем:

эс9-эс1 -у,

Ха - IT-I

У2-У1

yi(X3~Xt)

Пример. Вычислить корень уравнения ; 3*=5ж, находящийся между 2 и 3. Предва- ] рительно логарифмируем ур-ие, получаем: iclgS-Igjc-lg5=0. Вычисляем по таблицам .У1 (значение левой части при ж=2) и (значение при х=3). Имеем: 2/1=-0,04576; 2=+0,25527. Далее: Xi=2; Жа- 1=1 и t/2-?/i=0,30103; отсюда

о -0,04576 2 .f-p 0,30103 -А-2-й способ (способ Ньютона). В промежутке между Ж1 и ж 2 заменяем кривую касательной в той из крайних точек, где

отношение 7(у>0. Абсцисса ж4 точки пересечения этой касательной с осью ж и дает приближенное значение корня. При этом геометрически ясно, что истинное значение корня лежит между значениями, получаемыми этим методом и предыдущим (см. фиг.).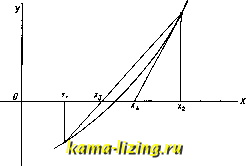

Приведем формулу для этого способа. Пусть точка ж 2 удовлетворяет вышеприведенному условию; обозначим значение производной в этой точке через у. Ур-ие касательной:

у-У2Уг{х-х; при г/ = 0, Ж4=Ж2 - ~ (для

точки Ж1 имели бы аналогично: 2-4=ж,- Пример. Берем то не уравнение:

= ж lg 3 - ]g л? - Ig 5; у = lg 3 -

Неравенству удовлетворяет точка

Жа = 3; у = 0,47712 - = 0,33236; ж. = = 3 - = 3 - 3-0,768=2,232. Итак,

истинное значение корня заключается между 2,15 и 2,23. Для лучшего приближения надо взять более близкие между собою значения Ж1 и Жа. Для приближенного решения алгебраическ. уравнений существует весьма удобный метод Греффе (см. Греффе метод).

Приближенное дифференцирование. По определению производной, f{x)=

= Иш; за приближенное значение мож-

но взять отношение д; теоретически это

отношение тем ближе к производной, чем меньше Дж; но на практике, если функция задана таблицею, при малых разностях, относительная погрешность увеличивается (см. вьппе), так что невыгодно брать самые малые из возможных по таблице приращений.

Пример. Вычислить

d sinx dx

при ж = 5°. Из

j:-10

таблиц имеем: Ду = 0,00289; Дж = 10 = ,

= г Вычисляем с помощью логарифмов:

lg Дг/= 3,46090; lg Дж = lg Jt-lg 1080 =

= М6373; Ig =1,99717; = 0,9935.

Приближенное вычисление Определенных интегралов. Т.к.

Jy dx измеряет площадь криволинейной трапеции, то его приближенное значение получится, если мы заменим искомую площадь прямолинейной трапецией:

Jy dx h

Погрешность дается выражением -

2-3 1-2

есть значение 2-й производной от у в нек-рой средней между Жо и Xi точке); она, вообще говоря, тем меньше, чем меньше h; поэтому, ft

если дан Jydx, где интервал Ь-а не очень

мал, вводим промежуточные точки деления: а=Жо, Xi, Ж2,...,ж,1=Ь на равных расстояниях h = ; обозначая значение у при

ж=ж<через у{{1=1, 2,..., п), получаем формулу трапеций:

J> dx { 42/0 + 1 + .Уа + + Уп-1 + -{Уп \.

а

Погрешность дается выражением -

(у -значение 2-й производной в некоторой промежуточной точке) и, как видно, она приблизительно пропорциональна h = г

Можно также разделить отрезок (а, Ъ) на четное число п = 2т равных частей и в каждом промежутке (Жз жг+а) заменить кри-

вую параболой второго порядка, имеющей те же ординаты, что и кривая в точках Хц, a?2f+i, 2*4-2; площадь, которая ограничена сверху дугой этой параболы, оказывается равной~{yi + + Уг1+ г). Для

всего интервала (а, 6) получим формулу Симпсона:

-j- 48 + ... + + 42/2Ж-1 + Угт)

Погрешность при этом оказьшается равной

{Ь-аУ у п* 5! 4!

И, следовательно, при увеличении п убывает приблизительно пропорционально 4-й степени h.

Пример. Вычислить In 2 = \ Берем

и=4; Л =;--0 = 1,0000; 2/1 = 0,8000; у =

= 0,6667; 2/8=0,5714, 2/4=0,5000. Приближенное значение интеграла будет:

1 (20 +431+ 22/2+ 42/3+ 24) = 8 0,6932;

таблицы дают: In 2 = 0,6931.

Дальнейшие методы приближенного интегрирования имеют своей целью дать возможность вычислять определенный интеграл, зная конечное число ординат, при помощи формулы вида:

А = Riyi + Riz + . + Ra>

где Ri суть одни и те же числа для любой функции у, зависяпще только от числа п [чтобы устранить их зависимость от длины интервала, мы вводим новое переменное t формулой:

преобразующей любой интервал (а, Ь) в интервал (-1, -f 1)]. К этой группе формул относятся: ф-ла Котеса, ее частные случаи- формула трапеций и ф-ла Симпсона, затем ф-ла Чебышева: +1

J fix) dx = [fixx) + fix,) + ...+ fix)], , -1

где значения функции берутся в совершенно определенных точках. При и = 2

-Ж1=-ЬЖ2 = 0,57735;

при п = 3

-Ж1 = я-з = 0,70711, Жг = 0; при п = 4

=0:4 = 0,79465, -Жг = = 0,18759; при п = Б

-Xj = Же = 0,83250, -х = ж = 0,37454, Жз=0 и т. д. Сюда же относится формула Г а у-е а, которая дает даже точное значение

интеграла, если fix)-многочлен степени не выше2м-1; в этом случае: при п = 2

-Жх = Жг = 0,57735, i?i = i?2 = -;

при W = 3

- aji = Жз = 0,77460, Жа = О, Rx = Ri = jg, при W = 4

= Ж4 = 0,86114, - Жа = Жз = 0,39998, 71 = 74 = 0,17393, R = i?3 = 0,32607. Приближенное вычисление неопределенных интегралов. Требуется найти значения FiX) =Jfix) dx для

переменного X. Поскольку точное выражение FiX) неизвестно, мы должны построить таблицу значений этой функции или ее график. Здесь мы остановимся на 1-м способе (2-й способ - см. Графическое интегрирование). Пртлженяи формулу трапеций. Дадим X следующий ряд значений:

Х-а; Xi=a-bfe,...; Xjfc=a-fM,... Получаем:

a+kh

ДХо) = 0;ДХ,)= J fix)dx

ТУ0 + У1+ +Ук-1-Ук

a+lk+l)h

FiXj,)= J fix)dx&

[io + yi+... + yk +2/fc+i откуда

FiXjx) = FiXj,) + Цу + Ук+г)-

Эта формула позволяет по значениям 2/о, Уг, 2/2. последовательно вьшислить FiX,), FiX,) и т. д.

Приближенное интегрирование дифференциальных у р-и й. Дано дифференциальное уравнение = fix,y);

требуется для разных значений ж вычислить значение того решения дифференциального ур-ия yix), к-рое при х=а принимает значение у = Ъ. Задача сводится к тому, чтобы при заданном (малом) приращении h независимой переменной вычислить приращение к, которое получает (ж). Идея метода Р у н г е состоит в том, чтобы выразить это приращение & в виде суммы:

RJt + RJc, + RJC3 + RJti,

где R-одни и те же для всех уравнений, а hi представляют значения fix,у) для некоторых определенных значений аргументов, умноженные на приращение h. Руиге дал несколько схем для значений R и для вычисления к; особенно он рекомендует следующую:

h = + \к, -Ь +

где величины Тс последовательно вычисляются по формулам:

\ = Да, 6)./ ; К = f{a + \-Ь Л-

Ф-ла оказывается точной для членов 5-го порядка относительно 7г. Исходя из полученных значений ai=a-i-h, bi=b-\-k, повторяем тот же процесс; получим таблицу для функции у(х).

Пример. g = ; при х=0, у = 1. Требуется найти значение у при х=0,2. Имеем:

а=0; Ъ = и 11=0,2; f(x,y)=~-Вычисляем:

kj =f{0;l)-0,2 = 0,2; k,=fiO,l; 1,1) = 0,154; 3=/10,1; 1,077) = 0,152; й;4-Д0,2;1,152) = 0,121; /c = 0,033 + 0,051 + 0,051-f 0,020 = 0,155.

Итак, при я;=0,2, t/ = l,155. Существуют и другие методы интегрирования: (например Штермера).

Лит.: Селиванов Д., Приближенные вычисления, Л., 1922; Крылов А. Н., О приближенных вычислениях, СПБ, 1911; Безикович Я. и ФридманА., Приближенные вычисления, Ленинград, 1926; Крылов А. П., Приближенное численное решение обыкновенных дифференциальных уравнений, Бер.яин, 1923; Runge С und К б п 1 g Н., Vorlesungen iiber numerfsche.s Rech-nen, Berlin, 1924. B. Степанов.

ВЫШИВАЛЬНОЕ ПРОИЗВОДСТВО имеет целью воспроизведение разнообразных узоров при помощи иглы и различного рода нитей, главн. обр. на тканях. Игла, прокалывая ткань и продевая сквозь нее нить, накладывает (закрепляет на ее поверхности) стежки, т. е. штрихи из нитей, тянущиеся от прокола до прокола, и, располагая их в известном порядке, постепенно переносит на поверхность ткани желаемый узор. Фоном Д.ЛЯ узора, кроме всевозможных тканей (цветных и белых), могут служить кожа, войлок и другие гладкие материалы. Нити, применяемые для вышивания, также представляют большое разнообразие: бумажные, шерстяные, шелковые, всех цветов и сортов, серебряные и золотые, блестки, бисер и т. п. По способу изготовления вышивки делятся на машинные и ручные.

Ручные вышивки. Группа ручных вышивок по характеру техники подразделяется на следующие виды. 1) В ы ш н-вание крестом, выполняемое по канве, наложенной на украшаемый материал. Этот вид вышивания, наиболее простой и распространенный, применяется к самым разнообразным тканям и выполняется одноцветными или разноцветными нитками, смотря по вышиваемому узору. По окончании работы канву выдергивают. 2) Вышивание полукрестом, т.е. выполнение креста только наполовину, представляет разновидность первого рода вышивки и применяется для более тонких работ. 3) Шитье гладью, применяемое главн. обр. для украшения белых тканей, заключается в тесном накладывании стежков, одного рядом с другим, по заранее намеченным контурам

рисунка. 4) Вышивание двойной гладью, т. е. воспроизведение узора стежками, одинаково покрывающими обе стороны ткани и образующими один и тот же узор с лица и изнанки, распространено далеко не так широко, как шитье гладью односторонней. 5) Ст р оч н о е ш и т ь е, получившее в настоящее время большое применение, вышивание по канве, образованной путем выдергивания нитей по счету и перевивания их клетками. 6) Ф и л е й н о е в ы-ш и в а н и е, имеющее некоторое сходство со строчным шитьем, заключается в воспроизведении узора на специально приготовленной для этого ткани, связанной из ниток и имеющей по своему виду сходство с канвой или сеткой. Для вышивания употребляются нитки одноцветные или разноцветные, смотря по вышиваемому узору.

7) Вышивание по плотной канве, образованной на украшаемой материи путем выдергивания нитей по счету, известное под названием шлезвиг-голштинского шитья, применяется гл. обр. для белых тканей.

8) Вышивки Ришелье-широко распространенное украшение тканей; состоит в обметывании петельным швом заранее намеченных контуров узора. По окончании работы пустые места между отдельными частями рисунка вырезаются, вследствие чего получается сквозной узор. 9) Ценной шов (тамбурное вьипивание), выполняемый в круглых пяльцах специа.1ьной иглой-крючком, применяется для украшения самых разнообразных тканей. 10) Ап-п л и к а ц и я-представляет собой особый вид вышивания. Узор, вырезанный предварительно из той же или другой ткани, обшивают шелком или нитками й нашивают на украшаемую материю; промежутки между отдельными частями узора часто заполняются вышивками иного вида. 11) Т я-желые вышивки восточного характера, гл. обр. золотые и серебряные, вышиваются рельефом, т. е. на намеченный контур узора накладывается настилка из ниток или тонких кусочков картона, густо покрываемая затем нитями.

Ручная вышивка в настоящее время занимает одно из видных мест в кустарной промышленности. Ее многочисленные узоры отразили самые разнообразные художественные течения, сохранив вместе с тем следы глубокой старины.

Богатые вышивки из шерсти, шелка, блесток, золота, серебра, камней применялись для украшения женских платьев и головных уборов. Большое разнообразие представляют и способы вышивания. Распространено было шитье двустороннее, наносившее одинаковый узор с обеих сторон холста; применялось шитье набором (бранью), своей техникой напоминавшее тканье; много вышивок выполнялось крестом (верх шов). Чаще всего встречалось шитье по перевити , т. е. по канве, образованной посредством выдергивания из материи нитей по счету и перевивания их в клетки (современное строчное шитьё). Разновидностью этого способа является шитье по письму , заключающееся в составлении узора из невыдернутых нитей. Много применялось шитье по вырези , состоявшее в вырезывании узора в холсте, при чем фон оставался гладким, и т. д. Разнообразные узоры, во множестве украшавшие предметы повседневного быта, немало способствовали красоте и нарядности бытовой обстановки.

Ручное вышивание с изобретением вышивальной машины стало вытесняться. Ручной способ изготовления вышивок, давая