получается

Если вместо С применяется эталоп переменной самоиндукции (вариатор самоиндукции), то, т.о., производится И. Ь Lg, при чем аналогичноЬд;=п2Ьэ.. Однако, найти Ьд. в этом случае мо-

jjmJ

\jiStSi3J

лево и при фиксированном L , при чем Ь Ь; для этого необходимо иметь переменный Сэ.. Действительно, из ур-кй

хкуЩь, и 1 =

= к УСдЬ,1 находится

Фиг. 3.

Из методов абсолютных наиболее употребительны в технике определения С и L по ф-лам закона Ома для переменного тока. Действительно, при схеме соединений (фпг. 4) получается (г в А , е в V, С в F):

Предполагается при этом, что конденсатор не имеет потерь; вольтметр д. б. статич. типа; при малых емкостях следует вводить поправку на параллельно включенную емкость

Ф 0. .л

Фиг. 4.

Фиг. 5.

вольтметра; технич. приборы по этой схеме дают точность И. до 0,5%. Аналогично д.чя И. самоиндукции (фиг. Ъ) имеем {L в Н):

~ id. < Ч.

Предполагается, что действующее активное сопротивление катушки мало сравнительно с (uL; вольтметр таклсе статич. типа.

Если первые предпосылки не имеют места, то требуется дополнительное измерение мощности, теряемой на исследуе.мом объекте; напр., при измерении L получается: а) по

схеме фиг. 5: z = ~-il,6) при измерении

мощности: R = Q ; отсюда L = -

Видоизменением метода замещения слулсит схема дифференциального трансформатора Хунда (фиг. 6). Индикатор включается во вторичную обмотку трансформатора; ток от источника питания проходит через две (первичные) обмотки; в одну из них включается последовательно переменный эталон (на фиг. 6 пшсазано И. емкости), в другую объект И.-конденсатор, емкость которого измеряется. Вариатор самоиндукции в цепи питания включается для настройки в резо-

нанс контура с источником эдс. При регулировании С и положения указателя R., таким образ., что индикатор (на фиг. 6 для примера показан детектор с гальванометром) устанавливается в нулевое положение, имеет место равенство измеряемой величины с соответствующим значением эталонной; так же определяется и активная часть общего сопротивления, самоиндукция, взаимоиндукция, сдвчг фазы и мощность.

И. диэлектрической постоянной е. Эти И. сводятся в технике к определению двух значений емкости конденсатора, диэлектриком которого служит сперва воздух (Cq), а затем - подлелсащее исследованию вещество (С); И. емкости производится по одному из описанных методов (в частности схемой моста Нернста). Искомая величина е=-

И. взаиАлоиндукции.

Чаще всего производят двукратное И. самоиндукции двух взаимодействующих систем (Li и Lg), при чем в одном случае они располагаются так, что магнитные потоки совпадают (Ь,), а в другом-прямо протнво-пололсны (-Lii); тогда из

имеем

M = (L,-Ln).

Менее распространен метод замещения. Возмолсно И. М путем сравнения с известной частью самоиндукции; измеряя амперметром

и в первой и во второй системах, М которых измеряется, из

находим

(О Mil =Ld2Co

М = L,

и е.

Аналогично, измеряя вольтметром ej получаем М = Li. Измерение рекомендуется производить при радиочастотах.

И. самоиндукции нонденсаторов и емкости катушек. Это И., встречающееся реже, производят приключением к конденсатору эталона самоиндукции L., имеющего величину L порядка измеряемой I конденсатора. В 1сачестве эталона рекомендуются фигуры из одного витка провода-их L легко вычисляется по Ф-ле Балсенова (см. Замкнутш1 антенна). Измеряется полученного хсонтура; если собственная во.чна коротко замкнутого конденсатора С (без эталона) есть Я, то

г-

При И., в особенности коротковолновых, необходимо учитывать емкость и самоиндукцию частей схемы (проводки, изоляторов, аппаратов и т. д.). Эквивалентную емкость частей схемы Со получают как увеличение емкости конденсатора С,к к-рому приклю-

чается параллельно; самоиндукцию частей схемы I находят из увеличения L контура, к к-ролгу I считается приключенным последовательно. Если исследуемая часть схемы обладает собственными I и С, то: 1) для И. Сц приключают к исследуемому объекту известную L, к-рая д. б. велика по сравнению с I объекта; 2) для И. I приключают конденсатор большой известной емкости (С Со). Измеряя в обоих случаях длину волны, находим пз основного ур-ия (3): в нервом случае Со, полагая С=0, т. к. l L, во втором случае I, полагая L=0, т. к. Со С.

При И. с различными частотами получают несколько отличное значение вследствие зависимости L и С от частоты. Вследствие уменьшения при возрастании / магнитного потока внутри провода, L с высокой частотой незначительно уменьшается; изменение L по этой причине учитывается коэфф-том {id {ш. Замкнутая антенна); кроме того, L какбы изменяется и потому, что имеется собственная емкость Со катушки; по последней причине кажушееся увеличение L я R учитывается по ф-лам:

L=Lo (1 - МСо)-; Д = jRo (1 - МСо)-\

где Ьц и Ro-значения для постоянного тока.

Емкость конденсаторов, при наличии в последних потерь, кажущимся образом уменьшается с возрастанием /:

= <о (l + = Со (1 + tg 8) = С + АС ,

где Со-калущ. емкость при любой частоте at, R-сопротивление, эквивалентное утечке (параллельно включенное сопротивление); еслп в конденсаторе существуют и диэлектрич. потери, то по этой причине изменение

С пропорционально . Наличие у вводов

конденсатора I таклее вызывает изменение С с частотой: С= Ссо(1 +со С1).

Емкость катушек Cq, представ.чяе-мая нами в виде конденсатора, включенного параллельно к безъемкостной катушке, измеряется или методом моста илп из собственной волны катушки. Исследуемая катухпка возбуждается генератором соответствующей частоты; волномером измеряется А; тогда

С = 253 - см. Практика предпочитает видоизменение этого метода в виде следующей экстраполяции: парал-.чельно катушке L включается переменный конденсатор С, и определяется длина волны об-})азованного пз L и С контура при каких-либо двух установках кон -депсатора С. Если нанести квадраты полученных длин волн в ф-ии от включаемой переменной емкости, то продолженная прямая АВ дает своим пересечением с осью абсщюс величину Cq, так лю как отрезок по оси ординат при С=0 дает квадрат собственной длины волны Я катушки (фиг. 7). И. коэфф-та связи дзух связанных цепей. 1)Путемрасчета из измеренных С, L, R и М,коэфф-т связи к определяется:

а) для индуктивной связи - k = -7- ,

b) емкостной

гальванической

Эти ф-лы дают однозначное определение при квазистационарном токе.

2) М е т о д о м И. падений н а п р я лг е-н и й на соответствующих частях связанных систем-см. Емкостная связь, Гальваническая связь. Индуктивная связь, Автотрапс-форлшторная связь. Связь.

3) Измерением частот с в я з а пн ы X колебаний (на фиг. 8 выбраны цепи с индуктивной связью). Контур I приключается к зуммеру t S, питаемому батареей В, а с контуром II весьма слабо связывается измерительный контур М с индикатором J; т. о. измеряются волны (частоты) связи /1, /а; затем контур II размыкается, и измеряется помощью контура М, связываемого слабо с /, собственная частота цепи /-fu совершенно аналогично находится собственная частота контура II-fiu отсюда

2 лШ-> (--м- ) = 9(Си -

7* Щ\1 с, Cxi

Расчеты значительно упрощаются, если контуры I я II с помощью конденсаторов С\ и с, настраиваются на ту лее резонансную частоту (fi=fu=f):

= ;.- я c-i c-Sl = c=-C .

/.f+л C с Ci + Ci Приблизительно считают, что

Фл/. 8.

/ - я - 2 Аналогично находим для емкостной связи: с,-с, 1 с,-с,

С + Са 2 С

И. частоты. Частота / излюряется числом периодов, или циклов, в секу!ду; icpoMe того, в практике измерений принято таклсе И. длины волны Я, связанной с частотой следующей зависимостью:

/(КЦ/СК.)-0,001/WcK.) = lg-?5£.

Практич. прибором д.чя И. частоты /, а следовательно, и длины волны Я служит ч а-стотомер - волномер, В1лючаемый главным образпм по одной из двух схем: волномер-вибратор и волномер-резонатор (см. Волномер, Частотомер я Индикаторы резонанса).

Абсолютное И. частоты и длины волн. Абсолютные способы дают Я и / независимо от других способов И. Я, т. е. при отсутствии эталонов Я и / применяются только в лабораторных условиях дли градуировки волномеров-эталонов , по которым узке градуируются технические

волномеры . Имеется . несколько абсолютных способов И. А и /. Естественным способом определения / и А является получение частоты в ко.чебательном контуре разряда эталонной емкости через точно известную самоиндукцию; при принятии всех поправок точность измерений получается по данным Гибе и Альберти ±001%. Возможно также применение машины высокой частоты, даюшей частоту по формуле

/ = 5 , где р - число полюсов, п - число

об/мин., определяемое по данным И. с точностью 0,1%.

Способ Лехера. Система двух параллельных проводов (фиг. 9) с перемычкой, или рейтером, в к-рый включен термогальванометр Th, возбуждается генератором высокой частоты. Получаются стоячие волны, при чем расстоя- , I t т ние между двумя смежен £ 0ГЛ а ;>: ными пучностями на-J I Т I 1 Т пряжений или токов равно половине длины волны. Американское бюро стандартов наш-.40, что способ Лехера дает частоту на 0,1- 0,5% больше истинной, так как скорость V распространения электромагнитной волны вдоль провода меньше скорости ее в пустоте с, а именно:

V = с (1 - zl) ,

и предложило ф-лу с поправкой / (кц/ск.) = i

откуда

/(кц/ск.) при чем

J = -

Фиг. 9.

1,4491- 10 I

В = -

I-расстояние между смелсными пучностями в см, Ro-сопротивление постоянному току одного см двойного провода в абсолютных электромагнитных единицах, а-расстояние мелоду проводами в см, d-диам. провода

в см, (o=2nf (/ в ц/ск.); если a d, то -6=

Практическая схема И. дана на фиг. 10.

Способ Мандельштама. Зуммер-ный контур на низкую частоту связывается с волномером (фиг. 11). В зуммерной цепи будет пульсирующий ток 1д с частотой /з . По теореме Фурье, этот ток распадается на ряд гармоническх переменных токов, т. е. с частотами, кратными /з. :

/ = /з.

Поэтому, если в волномере изменять непрерывно емкость, то волномер будет настраиваться на гармоники зуммерного контура, и в телефоне Т получится последовательный ряд максимумов звука. Пусть эти максимумы звука наблюдаются! при последовательном ряде значений конденсатора:

С=Со, Cl, С2,..., Cjc, они очевидно соответствуют некоторому последовательному ряду гармоник: / = т/,., (т + 1)/з (т + 2)/з., (т-Ь/с)/з.. Здесь к-число максимумов звука.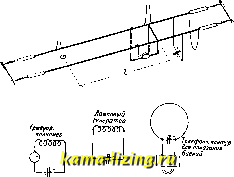

Фиг. 10.

полученных при И. Число к определяется по начальной и конечной емкостям конденсатора волномера

7П/,. =

(т-Ь /с)/з. =

2л У Ь-Ск

откуда посте де.чения имеем

m + h

окончательно

m = /с

Ус, - yck

Число /з. колебаний зуммера определяется вполне точно обычными методами акустики. Способ Мандельштама хорош для волн А 1000ле. Способ Лехера, наиболее употребительный для калибровки средних и коротких волн, дает хорошие результа- Л ты в диапазоне /-\ /-\

1 ж <А 1 ООО ж. О У \ / \ / \ / \t

весьма развившем- Фиг. и.

ся в последнее время применении пьезокварца как эталона частоты к градуировке волномеров см. Пьезокварц.

И. сопротивлений. 1)Из резонансных кривых. Для сравнимости резонансные кривые (см. Избирательность) следует строить приведенные, т. е. откладывая по осям величины

- и -

где ir и А,.-сила тока и длина волны при резонансе (фиг. 12). Теория Бьеркенса дает для односторонней расстройки

(5i -f (5 = 2 .-г

где (5i-логарифмическ. декремент контура, 2-логарифмический декремент волномера.