вление действующей силы совпадает с одной из главных осей сечения.

2-й с.чучай. Все действующие силы приводятся к моменту и главному вектору сил; в этом случае условия равновесия дают при малых углах d<p (фиг. 2):

-M + Sydx + MyO, (14)

где М-изгибающий момент в сечении I, Ml-в сечении II, отстоящем на бесконечно малое расстояние dx. За положительное направление момента принято то, которому соответствует вращение по часовой стрелке. При М> Ml

dM = M- My = Sydx,

Si = , (15)

т.е. главный вектор сил является производной изгибающего момента по х (теорема Шведлера) и называется срезывающей силой. Момент Mi компенсируется теми же

нормальными на-- пряжениями /с как и в случае отсутствия главного вектора . Существование последнего обусловливает появление напряжений касательных, лежащих в плоскости сечения. Т. о., в ка-ледой точке балки действуют касательные и нормальные напряжения. В длинных балках, в к-рых отношение длины I к высоте h (или диаметру балки d) больше 10, преиму-ш,ественное значение имеют нормальные напряжения; расчет ведут по формуле: j

В коротких балках (- = < следует делать проверку на касательное напряжение. Деревянные балки, благодаря слабому сопротивлению дерева сдвигу, обязательно д. б. проверены на касательные напряжения. Клепаные лселезные балки также д. б. проверены на касательные напрялсения т. к. площадь сечения их вообще мала и легко может оказаться недостаточной по отношению к касательным напряжениям. Ур-ием (8) устанавливается зависимость между ординатой прогиба балки и изгибающим моментом в данном сечении, именно

1 d.x м

Фиг. 2.

Фиг. 3.

образуемых X (фиг. 3),

При незначительных углах р, изогнутой осью балки с осью можно принять, что

1 (Ри

и дифференциальное ур-ие упругой изогнутой оси представится в таком виде:

Е I,

(16)

Двукратное интегрирование даст ординату

прогиба в функции ж. Подстановкой любого значения х определяется стрела прогибав точке с абсциссой х. Интерес представляет всегда наибольшая стрела прогиба, к-рая бывает в середине однопролетной балки или вблизи середины.

Частные случаи. 1) М = Const, т.е. изгибающий момент постоянен. По ур-ию (16) и (8) следует, что е = Const, или изогнутая ось балки представляет собой дугу круга. Стрелу прогиба получаем геометрически: для консольной балки

2£. /,

2) М = х (фиг. 3). Ур-ие изогнутой оси: Е I,

откуда

dy f

+ с.

Е 1,у = 2- -Сх + Су. Приж = 0: г/=0 и Cj = 0; при ж = : j; = 0

Поэтому

При х = 1

PJ. i8E-l\

3) При одновременном действии сосредоточенных сил и равномерно распределенных нагрузок количество постоянных в уравнении

Ьи1М111111111111Ш1ИШ

Фиг. 4.

Фиг. 5.

упругой кривой увеличивается на две для каждой области, и нахождение их, в виду сложности ур-ия, представлялось бы затруднительным. Число постоянных для всех случаев сосредоточенных и сплошных нагрузок, по теореме Клебша, м. б. сведено к двум. Для балки (фиг. 4) количество постоянных, подлежащих определению, равно двум; обе постоянные легко отыскиваются из выражений для конечных условий: а) у = 0 при ж = О и б)у=0 при х=1. К балкам (фиг. 5) теорема Клебша неприменима, так как в этом случае равномерно распределенная нагрузка не сплошная.

Косой И. Косым И. будет, если напра-в.пение действующей силы не совпадает с одной из главных осей сечения. На фиг. 6 направление силы совпадает с осью Y, а Z-- соответствующая главная ось Z-образного сечения: осиУ и Zg образуют угол <р. Разложением силы по главным осям Zq и Yq явление косого И. может быть сведено к И. в двух главных плоскостях-XY и XZ-под действием моментов

Mg = PI sin 9? = Mo - sin 9? и М = Mo cos<p. Напрялсение в точке к (ijo, z)

(17)

где 4 и - моменты инерции относительно главных осей сечения. Наибольшее на-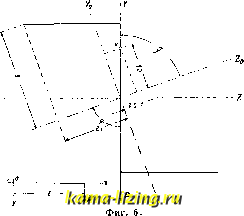

= 0 ,

пряжение в сечении оказывается в крайних его точках (напр. при г/о = б и = е) и равно:

, /sin ч> . cos рч

тах = -0 + -Wj (18)

Нулевое напряжение будет в точках, для которых

у sin . 2 COS9

2/о = - 30 ctg <р . (19)

т. е. все точки с нулевым напряжением ле-лсат на одной прямой, положение к-рой зависит от относительного значения главных моментов инерции сечения и расположения силы по отношению к г.чавным осям сечения.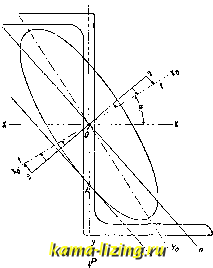

Фиг. 7

Нейтральную линию при косом И. легко найти построением. Построив эллипс инерции (фиг. 7), проводим в точке А пересечения

контура эл.чиг1са с направлением силы касательную к эллипсу и через центр сечения параллельную ей: это будет нейтральная линия теп, соответствующая ур-ию (19). Тр-к 0-1-2 изображает распределение напряжений. Расчетное ур-ие (18) для косого И. счужит . шшь для проверки напряжений в сечении: размеры сечения выбраны уже заранее по конструктивным соображениям или определены предварительно на тех лее основаниях, что и в случае изгиба в главной плоскости.

Криволинейный брус. При рассмотрешш брусьев, ось которых представляет плоскую кривую, обычно предполагают, что все внешние силы лежат в плоскости кривизны и что в той :ке плоскости лежит одна из главных осей инерции поперечного сечения бруса.

фиг. 8.

Брус, находящийся под действием сил, рассекаем плоскостью, перпендикулярной к изогнутой оси, и рассматриваем условия равновесия одной части. Внутренние силы взаимодействия отброшенной части можно привести к результирующему моменту Mg и силам JV и Q (фиг. 8). Силы Q (срезывающие силы) во внимание не принимают, полагая, что при этой деформации сечения бруса остаются плоскими (гипотеза Бернулли). Выделим из бруса бесконечно малый элемент (фиг. 9). Длина дуги А А = ({? + у) (1<р. Удлинение волокна АА равно AA=yd(p-\-SS, где SS- удлинение волокна, проходящего через ц.т. Относительное удлинение волокна АА будет

У (е + V)d<P (So + v)d<p или с некоторой погрешностью

Ь-ч + Ш. его

где io-относительное удлинение волокна, проходящего через ц. т. Напряжение в той лее точке А

Распределение напряжений происходит по пгаерболе и показано на фиг. 9 кривою CD. Из условий равновесия следует, что

J*fe,-dF=JV, (23)

Jk,-y-dF=Mf,. (24)

Подстановка значения к. дает:

Еу А d<?

Бг,Г +

0 (I

Гак как

о то

С и dF ,

J e7T = ~

(25a)

(26)

(27)

1ак как Eio = /<; , то

5 (256)

Из ур-ий 22, 2оа и 256 получаем выралеение для напряжения в .любой точке:

h 4~ -~>> -

QbF F

С V dF

( >°/. О

или, что то л-се,

к = л-- л- ь

- F q/f ((>o + y)l> Fh

Значение к можно найти для каждого сечения графическим путем (по Толле) или раз-лолеением в ряды. Для прямоугольника

Для круга Для трапеции

Здесь е означает половину высоты сечения, у- ie для крайних волокон, в к-рых напряжение достигает наибольшего полонштель-ного или отрицательного значения.

Предлагают рассчитывать кривые брусья также по ф-ле Фёппля (Foppl):

(28)

т. е. на сложное сопротивление; напр., крюки, рассчитанные по этой ф-ле, обнаруживают даже излишнюю прочность. Нейтральная линия перемещается от ц. т. сечения по направлению к центру кривизны О, и это перемещение возрастает с уменьшением отношения у° . Кривые брусья, для к-рых --5,

рассчитывают по формулам сложного сопротивления для прямо.линейных балок (брусья

малой кривизны). Брусья, для к-рых ° < 5,

называются брусьями большой кривизны; их следует рассчитывать iro ф-лам. выведенным для криволинейного бруса.

Деформация кривого бруса. Для определения перемещений отдельных точек кривого бруса под действием внехпних сил удобнее всего по.льзоваться теоремой Ка-сти.льяно; для этого нужно иметь выра?кение потенциа.льной энергии бруса в виде функции от внешних сил. Возьмем точку криволинейного бруса В{Хо, ?/о) в первоначальном положении. После деформации ее поло-;кен1ге будет А (х, у). Необхолиио узнать приращения x и iy координат и угол поворота Лер В точке В. В общем случае на сечение бруса будут действовать изгибающий момент и продольная сила. Найдем выражение пбтенпиальной энергии. Момент Ж вызовет приращение угла df на ве.личпну Adg?, определяемую ф-лой

и совершит работу dT =

М Д d<p ds

2 2 Els

Потенциальная энергия при действии одного мохмента будет

J 2£/з

Продольная сила JV изменит угол d(p на величину, определяемую ф-лой

Ndq> EF

При этом приложенный ранее момент совершит работу

1гт1 MNdv MNds

dTy = М Adg> = =

Продольная же сила создает потенциальную энергию:

NX Nds 2 ~ 2EF

Полная потенциальная энергия под действием момента и продольной силы будет

J 2Е1г J EFq J 2EF

Для брусьев малой кривизны это уравнение упрощается, т. к.

-EFf

Б. ч. при решении задач пользуются ф-лой

J 2Е1г

Интегрирование распространено навесь брус. Искривление бруса будет вполне определено, если для каждого поперечного сечения известны перемещения его ц. т. и угол поворота. Положим,требуется исследовать деформации бруса, закрепленного нижним концом (фиг. 8). Чтобы найти угол поворота сечения под действием внешних сил, нужно к заданным нагрузкам присоединить фиктивный момент т, приложенный в рассматриваемом сечении, и составить производную от потенциальной энергии бруса по т. Ур-ие потенциальной энергии выразится:

~ J 2Е1г J EFe J 2EF

Возьмем части, производную по фиктивному