менньш количеством рабочего тела и потому является необратимым. Для рассмотрешгя от-де.71ьных циклов, осуществляемых в Д. в. с, введем следующие общие понятия и обозначения для всех циклов. Рабочим объемом ци.яиндра Vj назовем объем, описываемый поршнем между его крайними мертвыми положениями; объемом пространства сжатия -объем, в к-ром заключена рабочая смесь в конце слсатня при положении поршня в мертвой точке; сумму объемов V+Vh обозначим через F . Степенью сжатия е назовем отношение объемов в начале и в конце

слсатия е, степени предварительного расширения Q и степени увеличения давления Я. Если в указанной формуле подставим = 1, то смешанный цикл превращается в нормальный, т.н. цикл О т т о, и

Из этого выражения для щ, выведенного в нредположении постоянных теплоемкостей, видно, что термический кпд зависит исключительно от степени слсатия а и показателя к, с повышением которых он растет. Зависимость от е и к дана в табл. 4.

Табл. 4. - Кпд щ для цикла быстрого сгорания (Отто)прираз.дичных е и к.

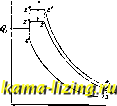сжатия,т.е. = Объем идав.яениев конце сгорания обозначим соответственно через Fj, и 2j. Степенью увеличения давления при р\ и сгорании Я, если оно

имеет место, назовем отношение давлений в конце и в начале

сгорания, т. е. Я = .

Степенью предварительного расширения Q назовем отно-Оз шение объемов в конце и в начале сгора-

- ния,т. е. ? = . То-

гда степень расширения 8, представляющая отношение объемов в конце расширения и в конце сгорания, выразится так: о = ~

Термический кпд. Как общий случай рассмотрим рабочий процесс, в к-ром часть тепла (1 Cal сообщается по линии г; = Const, другая часть §2 Cal-по линии р = Const; холодному источнику отдается Cal (фиг. 8). Термический кпд

Выразив тепло через температуру и теп.ло-емкость Qi=c,(T,-T,), д2=(Т,-Т,), (Зз = с,(Т - TJ и вставив эти выражения в ур-ие (21), получим:

t=~ Y--Tc\h{T,-Tz)

Выразив все темп-ры, входящие в это ур-ие, через темп-ру Т, пользуясь вышеприведенными обозначениями и ур-иями адиабаты: Т,Т,е-\ Т, =1Т,=и-Та, T.qT. =Qle-T,

получаем после подстановки:

= 1 - Ihl л - 1 + кХ(в- 1) *

Т.о., термический кпд смешанного цикла зависит от показателя адиабаты к, степени

Из табл. видно, что с повышением к при одном и том же е термический кцд возрастает; такая же зависимость существует между % и е при одной и той же величине к. Подставляя в ф-лу (23) Я = 1, получаем кпд для так называемого цикла Дизеля

е*-1

1

fe(e - 1)

Из этого вырал-сетшя видно, что для двига-те.тя Дизеля термический кпд зависит, кроме е и Л;, еще от степени предварительного расширения q. Чем больше q, тем меньше и так как р увеличивается с ростом нагрузки, то щ Дизеля повышается по мере убывания нагрузки. Зависимость щ цикла Дизеля от £ и Q приведена в табл. 5.

Табл. 5. - К п д щ цикла различных е., k

Дизеля

п. q.

Для определения влияния отдельных факторов на термический кпд и их взаимные отношения необходимо проследить изменение термическ. кпд в зависимости от одной лишь переменной, в то время когда другие величины имеют какие-нибудь постоянные значения. Основной вопрос, который возникает у исследователя: каким образом должно быть подведено тепло для того, чтобы обеспечить максимальное его использование. В смешанном цикле это тепло состоит из тепла, сообщенного по v = Const и по p = Const. Предположим,.,что количество тепла Qi-b §2 не меняется, а меняется лишь относительное зна-ченпе Qi и атак что сумма Q = i+2 = = Со list. Имеем:

Qi = сЛТ, - т,) = с,Те -1)=С,Т,(Я -1), Q,= Ср{Т,-Т,)СрТ, (4-l) =CpT,iQ-l), о,ТЛ7.- 1) + срТЛя-1) = Const, 9+ =;. ! + ы{{> - 1) = Const. (24)

При постоянной теплоемкости и постоянной степени сжатия, с и Т суть величины постоянные, и вся левая часть уравнения также постоянна. Полученное выражение (24) позволяет при постоянном сообщении тепла определить связь между ). ж д. Задаваясь

iO II t,2 1,3 j.4 },5 1,6 1,7 1,8 1,9 2fi 2J2;l2Z4 2.S 2,6 2,72,823,03,ГЗ,г 3,3 3/43,5 6 SJ8 X

Фдг. 9.

разными значениями д.т1яЛ, определяя соответствующие им значения q при данном количестве сообщенного тепла и подставляя полученные значения в ф-лу термического кпд (23), найдем изменения % при выщеуказанных условиях, изображенные на фиг. 9. Здесь жирные кривые соответствуют термическому использованию при постоянном сообщении тепла, в зависимости от изменения-р и Я, а тонкие кривые в зависимости от изменения Л и количества сообщенного тепла,- при постоянном Эти кривые построены для степени сжатия £ = 15 и показателя /с = 1,4. При Я = 1 получим значения щ для разных Q, которые соответствуют нормальному циклу Дизеля; при (> = 1 получаем значение щ для цикла Отто. Так. образом, с левой стороны диаграмма ограничена вертикальной прямой Я = 1, а сверху-прямой ()=1. При постоянном количестве сообщенного тепла смешанный цикл, по мере удаления от цикла Дизеля и приближения к циклу Отто, повышает кпд. В пределе, когда все тепло сообщается по f=Const, термический кпд, независимо от количества сообщенного тепла, для всех кривых получится одинаковым. Если, при данной степени предварительн. расширения

Фиг. 10.

увеличить X за счет большего сообщения тепла, то Tjt последнего цикла несколько увеличится. Таким образом, кпд диаграммыасгге меньше кпд диаграммы acz zei (фиг. 8). На фиг. 10 представлены изменения кпд в зависимости от практических изменений и Я в пределах ()=2,0--3,0 иЯ = 1,0Ч-1,3, как они имеют место в двигателях, которые работают по этому циклу.

Сравнение циклов при постоянной и переменной теплоемкостях. Зависимость величины щ от состава рабочей смеси при постоянной и переменной теплоемкостях представлена графически на фиг. 11 и 12, при чем первая относится к случаю с = Const, а вторая- к с переменному. По оси абсцисс отложены величины теплотворных способностей смеси и соответствующие им отношения количества газа к воздуху, а по оси ординат-величины щ, темп-р Т и давлений р рабочего цикла. Сравнивая кривые этих двух диаграмм, видим, что при с переменном падение щ по мере обогащения смеси резче, чем при с постоянном. Для коэффициента смеше-1П1Я Vso (соответствующего 161,3 Cal) значения % для обоих случаев мало разнятся друг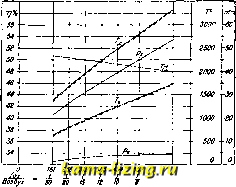

W Приток твпм <Ы

Фиг. 1 1.

ОТ друга (50,5 и 49%),тогда как для смеси богатой (Ve) разница достигает 7% (48 и 41%).

Из рассмотрения каждой из этих диаграмм в отдельности можно проследить зависимость р и Т начала и конца расширения от состава смеси. По мере обогащения сме-си,р и Т соответственно возрастают, вследствие чего увеличивается теплоемкость рабочей смеси, уй1еньшается /с и понижается термическое использование в двигателе, что видно и из вырансений:

% = 1 -

(Отто)

ft(o-l)£fc-(Дизель

Следовательно, для данного рабочего тела кпд находится отчасти в обратной зависимости от температуры. Т. о., и здесь подтверждается заключение, что при определен-,ной наивыгоднейшей степени сжатия е работать с бедной смесью лучше, чем с богатой.

1> tS) гзв 3№ 3S5 454 555

h h h h J

Фиг. 12.

Приток тепукг в Cal

Цикл Otto (при е:? Const). Даны s и состояние точки а (фиг. 13); рабочий цикл совершается двухатомным газом. По уравнению адиабаты, при cjtConst,

е~ V K-i)\Va) fe -l

(25)

определяем температуру в конце сжатия Т. Зная количество сообщенного тепла Q, определяем температуру вспышки Т по ур-ию

Qi + (а, + Т,) Т, = (а, + Ь, Т, )Т при чем все значения и {а + ЬТ) м. б. взяты по отношению либо объемных, либо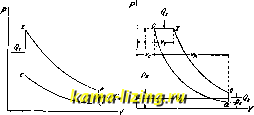

Фиг. 13.

Фиг. 14.

весовых единиц, а Ь, относится к средней теплоемкости. Температуру в точке е определяем по ур-ию адиабаты:

(>-а)©

ft. - 1

(>-а)

Зная температуры рабочего цикла, находим термический кпд:

Q2 i lav + bm(Ta + Te)] (Tt-Ta)

*=1-=1-J

Для примера определим кпд при постоянных и переменных теплоемкостях для цикла Отто, для степени сжатия е=5, при сообщении 500 Cal тепла на 1 кг рабочего воздуха, при начальном состоянии воздуха, соответствующем точке а, 1 atm и 300° К. При с = Const

При с Const для воздуха

fc= 1,422-

0.572 I, 1 400. 0,572

10 000 О-1,422, г-

522- = Л 0.572-300 \ Тс \ 0,422 - 10 OOOJ

0,572-300

5 * 0,422-10 ООО

откуда Т,= 568°.

Пишем уравнение сгорания, относя все величины к 1 кг-мол.: для воздуха (/м=29)

= . 500 = 29 500; а + ЪТ = 4,625 + +0,00053Т; 29 500+(4,625-f-0,00053 568)568 = = (4,625 + 0,ОООЪт\)Т откуда Т, = z 8304

Для адиабаты расширения имеем:

2 83 л 0,572-2 830 у о 4.33 , 0,572 - 2 830 . Те [ 0А2г 10 000/ 0,422 10 ООО

~ 1,599; Т, =1770;

[4,625+0,00053(300 + 1 770)](1 770-300) .1 f]t=l--------------------=0,421.

Цикл Дизеля (при с Const). Даны () и е и состояние точки а; цикл совершается двухатомным газом (фиг. 14). Как и в цикле Отто, характерные температуры Т , Tg и Tg можно последовательно определить из следующих уравнений:

= (l 11:ёЛ J 4-

с \ К - 1/ ft. - 1

Т,= ?Т,;

Ve\ft.-1 , гГг vj ft.-l

ft - 1

На основании полученных температур термический кпд двигателя выразится:

Q. [ар + Ьш{Тс+ Т,тТ,-Тс)

Сравнивая кпд для цикла Дизеля при постоянных и переменных теплоемкостях, например, при в=15, q=3 и начальном состоянии воздуха 1 atm и 300° К, аналогично получаем: при с = Const, 0,567; при ctConst, %= 0,503.

Сравнение кпд циклов в тепловой диаграмме. Весьма наглядное представление об использовании тепла в теоретич. циклах дает тепловая диаграмма. С повышением степени сжатия кпд увеличивается, что видно из фиг. 15, где площадь acze соответствует полученной работе при данной степени сжатия. С повышением степени сжатия и, соответственно, температуры сжатия до точки с, весь избыток тепла cczz, дополнительно введенный в рабочий цикл, идет на совершение работы. Теоретические циклы, ограниченные двумя адиабатами и изонлерой отдачи тепла, при разных способах подвода тепла по р = = Const, i;=Const, T=Coi)st, дают разные тепловые эффекты, в зависимости от параметров. За основной исходный параметр м. б. взяты либо постоянная степень сжатия либо максимальное давление. На фиг. 16 представлены три

[а + Ь ,(Те + ТатТе-Та)

Фиг. 15.