вольной замкнутой поверхности, некоторой производится интегрирование, п-внутренняя нормаль к элементу поверхности, с- скорость света, d<f-элемент поверхности, гр(0)-значение гр в данной точке. Вполне точное решение задач о распространении волн в среде, в частности задач диффракции, достигается непосредствен, решением волнового уравнения при данных граничных условиях. Этот прием представляет,-однако, очень бстьшие математические трудности.

Лит.: Хвольсон О. Д., Курс физики, т. 2, Берлин, 1923; Френель О., О свете, Москва- Ленинград, 1928; Drude Р., Lehrbuch der Optik, Leipzig, 1913; Huygliens Ch.. Traite de la lu-miere, Paris, 1920; P о in car 6 H., Theorie mathe-matique de la lumi6re, v. 2, Paris, 1892: Planck M.,Einmhrung indie theoretische Physik, B. 4, Leipzig, 1927. H. Фредерике.

ГЮЛЬДЕНА ФОРМУЛЫ, ф-лы для определения поверхностей и объемов тел вращения. Г. ф. выражают собою содержание следующих двух теорем.

1. Величина поверхности S, образованной вращением какой-либо плоской кривой около оси, лежащей с ней в одной плоскости и ее не пересекающей, равна произведению длины L этой образующей линии на длину дуги, пройденной ее центром тяжести. Обозначая через Xq расстояние центра тяжести образующей линии до оси вращения, получим для всей поверхности тела вращения: S = 2жхоЬ; для части же поверхности, соответствующей угловому перемещению а,меньшему 2л, S = aXoL.

2. Величина объема V, образованного вращением какой-либо плоской фигуры около оси, лелсащей с ней в одной плоскости и ее не пересекающей, равна произведению образующей площади F данной фигуры на длину дуги, пройденной ее центром тяжести.

Обозначая и в этом случае через Хд расстояние ц. т. образующей площади до оси вращения, получим для всего объема тела вращения: V==2t[XqF; для части объема, соответствующей угловому перемещению а, меньшему 2лг, V=aXoF. Если ось вращения пересекает площадь данной фигуры, то вышеуказанная формула определит разность объемов двух тел вращения описываемых площадями частей фигуры, лежащими по ту и другую сторону от оси вращения. Если вообще меридиональная линия дана уравнением г/=Дж), ось Ох есть ось вращения, S-часть поверхности тела вращения, заключенная между двумя плоскостями, проведенными на расстоянии Xi и х от начала хсоординат нормально к оси ж-ов, и V-объем, заключенный между теми же плоскостями и поверхностью тела вращения, то

S=.2ny(U; V=7tJ2/2dx,

a;, о:,

где dl = Ydx + dy-дифференциал длины дуги меридиональной кривой.

Вышеприведенные Г. ф. могут быть применяемы и вообще к какому угодно движению ц. т., лишь бы площадь фигуры была всегда перпендикулярна к направлению движения, напр., при образовании различных трубчатых поверхностей и объемов. Две теоремы, лежащие в основе форму.1 Гюль-дена, изложены Гюльденом (Guldin, 1577- 1633гг.) в его трудах: De centre gravitatis и Centrobaryca , но еще раньше эта же идея об определении поверхностей и объемов тел вращения встречается у греческого математика Паннуса (Pappus, Collectiones ma-thematicae, lib. VII). A. Яшиов.

ДАВИЛЬНЫЕ СТАНКИ служат для изготовления из листового металла полых предметов, которые представляют собою тела вращения. Выдавливание заключается в том, что на головке щпинделя а Д. с. (фиг. 1), представляющего собой несколько измененный простой токарный станок, закрепляется модель b (лучще всего из пальмового дерева), которая имеет очертания внутренней поверхности изготовляемого изделия. Отрезанный на круговых ножницах или на щтампе диск с из обрабатываемого металла соответствующего диаметра прижимается к модели при помощи наконечника d (на центре задней бабки) и затем нажимается на вращающуюся модель при помощи стального ролика е или друг, соответствующего инструмента (фиг. 2).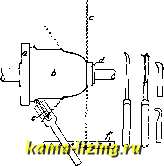

Фиг. 1.

Фиг. 2.

Такое нажатие производится вручную, для чего станок снабжается подручником / с рядом отверстий, в которые по мере надобности вставляется штифт, который служит опорой для давильного инструмента (вместо таких подручников иногда применяются специальные супорты). Перемещая давильный инструмент вдоль модели, диску постепенно придают требуемую форму. В случае выда-в.11ивания более сложных форм операцию производят в несколько приемов, пользуясь последовательно промежуточными моделями, при чем материал в виду наклепа иногда приходится отжигать.

Ход работы на Д. с. (производство металлич. абажуров) представлен схематически на фиг. 3. Металлический кружок соответствующих размеров приставляют к модели и слегка прижимают к ней указанным выше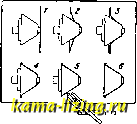

Фиг. 3.

способом (фиг. 3, 1); затем станок пускают в ход, и кружок центрируется легким нажатием на его кромку деревянного бруска, после чего наконечник (на центре задней бабки) прижимается к кружку плотнее и закрепляется в этом по-лолхении. Давильщик слегка протирает вращающийся кружок куском воска или мыла, вставляет в соответствующее отверстие подручника штифт

и приступает к работе, как было указано выше (фиг. 3, 2-б). Во время работы иногда приходится выравнивать кромки такого кружка при помощи особого резца (в виду растягивания материала при его выдавливр,-нии). Загибание бортика производится при помощи инструмента, головка к-рого представляет собою шарик соответствующего радиуса; край отверстия (с правой стороны) отворачивается и обрезается. На фиг. 4 приведен пример выдавливания пустотелого предмета с внутренней стороны. Для этой цели на втором супорте 1, который установлен впереди обрабатываемой заготовки 2, укрепленной при помощи державки 5, помещают ролик 3, представляющий собой обратную (негативную) форму изготовляемого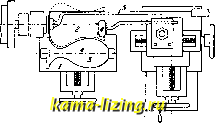

Фиг. 4.

предмета, и при помощи давильного ролика 4 нажимают материал на форму 3. Обычные скорости станка: для железа толщиной 1 мм-500 об/м., для цинка-от 1 ООО до

1400, для меди, латуни и алюминия - от 800 до 1 400. Для выдавливания, в отличие от прессовки, требуются рабочие более высокой квалификации, но зато для него не требуется изготовления дорогих штампов и приспособлений.

Лит.: Machinerys Encyclopedia, v. 5, p. 453-460, N. Y., 1917. В. Пальм.

ДАВЛЕНИЕ на поверхности тела, нормальная составляющая суммы сил, приложенных извне к телу, приходящаяся на единицу поверхности. В случае неравномерного распределения нормальней составляющей, Д. в разных точках поверхности опре-

деляется как (сила приложенная на бесконечно малом элементе площади), где N- нормальная составляющая суммы внешних сил, S-величина поверхности, к которой эти силы приложены.

В твердых телах давление вызывает изменение формы и объема и одновременно силы реакции тела. При установившемся равновесии, когда изменение формы и объема прекратилось, сила Д. в каждой точке поверхности тела уравновешивается равной и противоположной силой противодействия тела (действие равно противодействию-3-й закон Ньютона). В упругом твердом теле, при наличии давления, внутри тела действуют упругие силы напряжений, зависящие от величин упругих деформаций, претерпеваемых телом. В изотропных упругих телах упругие силы напряжений определяются в каждой точке тела помощью тензора напряжений; в кристаллических твердых телах - при помощи тетрады на-прянсений (см. Векторное исчисление и Упругость).

Для совершенных флюидов (газов и жидкостей) введено понятие о Д. внутри флю-идсв. Если мысленно расположить внутри флюида площадку, проходящую через данную точку, и обозначить обе стороны этой площадки через 1 и 2, то со стороны 2 внутри флюида на нее действует нормальная сила jF , равная и противоположная силе, действующей на ту же площадку со стороны 1. Величина силы F не зависит от ориентации площадки. Д. р в данной точке флюида, по определению, называется сила, действующая на единицу площадки, т. е.

Если в совершенной жидкости мысленно провести некоторую замкнутую поверхность S, ограничивающую объем т, то

р dS J\7p dr ,

где р-давление, а Vp-вектор силы, действующей на единицу объема и уравновешивающей давление (см. Векторное исчисление, теорема Гаусса). Д. внутри весомых жидкостей при равновесии зависит поэтому от положения точки по отношению к уровню жидкости (см. Гидростатика). В газах, заключенных в замкнутых сосудах, давление одинаково не только в каждой точке по всем направлениям, но и во всем пространстве, занимаемом газом, если пренебречь его весом (см. Газ и Кинетическая теория г а-

г. э. т. VI.

зов). Избыточным Д. газа называется разница между давлением газа, заключенного в замкнутом сосуде, и давлением среды, окрулсающей этот сосуд.

За единицу давления в системе CGS принимается бария, равная давлению 1 дины на 1 см, и ба р = 10* бариям. В настоящее время в качестве практической единицы Д. во Франции и в СССР введена п и э з а, равная Д. силы в 1 стэн на 1 (пиэза=10* бариям). В технич. системе метрическ. единиц за единицу Д. принимается Д. силы в 1 кг на 1 cjvt (1 кг1см = 98,1 пиэзы). В англ. системе мер единицей Д. является Д. си-ды в 1 фн. на 1 дм.- (Д. 1 фн. на 1 ДМ.2 = 0,070307 кг/см; Д. 1 ш на 1 дм. = 157,488 кг/см).

В гидравлике Д. измеряется вм водяного столба; Д. 1 jn вод. столба равно Д. силы в 0,1 кг/см. В учении о газах употребляют- ся в качестве практическ. единиц Д.: 1) м е-трич. атмосфера: (1 atm = l кг/см = = 98,1 пиэзы; не смешивать с нормальной атмосферой, - см. Атмосфера); 2) Д. 1 см столба ртути при 0° (1 см Hg = = 1,333 пиэзы); 3) Д. 1 см вод. столба при 4° (1 сж вод. столба = 0,0981 пиэзы=0,001 кг/см).

Для измерения Д. выше атмосферного служат манометры (см.), для измерения Д. атмосферы употребляют барометры (см.), для измерения Д. ниже атмосферного применяют вакууметры (см. Манометры).

Приведем несколько величин разных Д.: Д. остающихся газов в пустотных лампах 10~в см Hg; то же в катодных лампах и рентгеновских трубках-10 cjvt.Hg.; Д. газа в городских газопроводах 1-1,5 см вод. столба; давление пороховых газов в каналах орудий около 8 ООО кг/см.

Лит.: Хвольсон О. Д., Курс физики, т. 1, 3, Берлин, 1923; Кирпичев В. Л., Сопротивление материалов,М., 1923; Шпильрейн Я. Н., Векторное исчисление, Москва-Ленинград, 1925; I g п а-t о W S к у W., Die Vektoranalysis und ihre Anwendung in der theoretischen Physik, B. 2, Leipzig, 1926; P 5 p p 1 A., Vorlesungen iiber technische Mechanik, B. 3, 10 Aufl., Leipzig-Berlin, 1927; F6ppl A. u. F6ppl L., Drang und Zwang, B. 1, 2 Auflage, Munchen-Berlin, 1924, B. 2, Munchen-Berlin, 1920; Keck W., Vortrage uber Elastizitatslehre, B. 1, Han-noyer, 1922. Д. Виннер.

ДАЛЬНОВИДЕНИЕ, телевидение, электрическая телескопия, передача на расстояние изображений движущихся предметов посредством электрич. сигналов, распространяемых по проволоке или через радиостанцию. Передача на расстояние изображений неподвижных предметов (рисунков, фотографий) носит часто название телефотографии.

В основу Д. положено использование двух аппаратов-передающего и приемного, связанных между собой посредством проволочной линии или радио. Основной системой передачи изображений, действительной для всех современньЕх аппаратов, применяемых в рассматриваемой области, является т. п. точечная система. Она заключается в том, что в передающем аппарате в процессе самой передачи изображение оптическ. путем разделяют на большое число отдельных площадок ( точек ), которые воздействуют в последовательном порядке на прибор, превращающий световые импульсы в электрическ. {сж. Фотоэлемент); последние затем распространяются по проволоке или излут1аются