Более точный метод решения диффрак-ционных задач дан Кирхгофом. Объемную волновую функцию Ф, удовлетворяющую волновому ур-ию, Кирхгоф при помоши теоремы Грина сводит к функции на произвольной поверхности, охватываюш- данную точку наблюдения. Значение волновой функции в этой точке, но Кирхгофу:

*.= i [K)-eos( r)l(-)]clS.

где интегрирование производится по всей указанной поверхности S, г-расстояние

Фпг. 2.

нек-рой точки поверхности от точки наблюдения, п-внешняя нормаль к поверхности; в подинтегральной функции, в Ф, время i

заменено через у, где с-скорость света.

Приведенная ф-ла и заменяет полностью принцип Гюйгенса-Френеля, являясь, в от-.1ичие от последнего, вполне точной. Однако, при практическом применении к диф-()ракционным задачам и этот метод не дает безукоризненно строгого решения; для этого требуется точное знание значений Ф и

на вспомогательной поверхности; в действительности же относительно этих функций приходится делать приближенные более или менее вероятные предположения, что удается довольно точно сделать в отношении коротких волн и трудно выполнимо для длинных.

Наконец, точное решение диффракцион-ных задач принципиально м. б. получено непосредственным интегрированием уравнений Максвелла при данных граничных условиях. Задачи такого рода весьма трудны и решены только для немногих простейших случаев. По мере усовершенствования теории получается все более Tecfioe согласие теории и опытных данных, при чем для лучей, диффрагированных под большими уг-.лами по отношению к первоначальному направлению (Д. Гун), необходимо прибегать к точным методам. Современное развитие квантовой волновой механики (де-Бройль, Шредингер) позволяет надеяться, что клас-сическ. волновая теория диффракции света почти целиком (по крайней мере в отноше-

нии ее математического остова) может быть перенесена и в квантовую теорию света.

Диффракционные решетки. Явление Д. используется для разложения света в спектр в диффракционных решетках. Последние состоят из большого ряда щелей, расположенных на равных расстояниях и разделенных непрозрачными промежутками. В простейших диффракционных решетках щели получаются алмазной штриховкой плоского стекла посредством делительной машины. С таких решеток могут получаться целлюлоидиые реплики. Простую плоскую диффракционную решетку можно также получить, фотографируя в значительно уменьшенном масштабе соответствующий чертеж. Диффракционные решетки для больших спектральных установок делают не для проходящего, а для отраженного света; штриховку нан9сят на сферических вогнутых поверхностях из зеркального металла. На таких решетках, достигающих 15 и 6o.7iee см в диаметре, посредством делительной машины, сконструированной Роуландом и усовершенствован. Майкельсоном и Вудом, удается наносить сотни тысяч штрихов (1 ООО-1 500 на мм). При работе с вогнутыми отражающими диф-фракционными решетками становится излишним нрименение линз, сама решетка фокусирует спектры; благодаря этому возможно изучение в вакууме спектров крайнего ультрафиолетового света от 100 до 10 m/t, который поглощается в кварце и флюорите (Милликен). Действие диффракционных решеток как спектрального прибора основано на Д. света от каждой щели в отдельности и на интерференции света, исходящего изо всех щелей. Теория диффракционных решеток для простейшего и практически важного случая Д. Фраунгофера (см. выше) может быть получена различными методами как на основании предположения о совершенной независимости монохроматических компонентов сложного света (ньютоновская смесь цветов), так и на основании учения о белом свете как некотором импульсе, который гармонически разлагается периодической диффракционной решеткой.

Теория приводит к такому выражению для интенсивности диффракционной картины в данной точке ноля:

где Jo-постоянная для данного случая величина; а-ширина щели; 8-постоянная диффракционной решетки, т. е. расстояние между центрами двух последовательных щелей, fi=sin(p, где (р - угол Д.; п - число щелей. Указанная функция представляет ряд чередующихся максимумов и минимумов. Основная группа тех и других, имеющая наибольшее значение при боль-

i ших п, определяется равенством (л6= ,

где к-ряд целых чисел. При JjaBnoM О или целому кратному от п получаются максимумы, в остальных случаях-минимумы.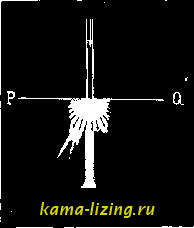

Диффракционные картины: 1. При прохождении парал.кльных лукй через широкое отверсто. 1. 1о же черен узкое 0 11?ергтие. 3. При прохождении спета через клиновидную 1нел1,. 1. То же через мато1 огворстие. 5. Тень конского г.олоса. G. Течь ма.ченького диска.

Помимо указанных максимумов и минимумов имеются и другие, но значение их при большом п и надлежащем выборе отношения ничтожно. Обозначим: к=т -п, где

т=0,1, 2 ... , и введем значение в написанную формулу для максимумов; тогда она

выразится в таком виде: sm(p = . Для

ш = О положение максимума не зависит от длины волны, получается неразложенное изображение коллиматорной щели (спектр нулевого порядка), для т=1, 2,... положение максимума зависит от Я, и свет разложится в спектры (спектры 1-го, 2-го и т. д. порядков) по обе стороны от спектра

нулевого порядка. Из ф-лы 81п<р=для

(> Я .яегко видеть, что длина спектра 2-го порядка будет вдвое больше, чем 1-WFt. д. Отношение длин волн крайнего красного и крайнего фиолетового в видимом спектре приблизительно равно 2, поэтому спектры 2-го, 3-го и т. д. порядков будут все больше налагаться друг на друга, только спектр 1-го порядка останется чистым. Если, наоборот, Я >6, то, как можно видеть из формулы sin (р , никакого спектра, помимо

неразложенного спектра нулевого порядка, получиться не может. Поэтому кристалл, являющийся в сущности пространственной диффракционной решеткой, благодаря правильному расположению молекул не дает никакого диффракционного спектра при пропускании видимых лучей, но обнаруживает Д. для лучей Рентгена с короткой волной.

Характеристикой оптич. качеств диффракционной решетки служит ее разрешающая способность. Таковой называется отношение длины волны Я к наименьшей разности длины волн ДЯ двух соседних спектральных линий, которые еще воспринимаются как отдельные линии. Из уравнения диффракционной решетки следует, что д= т. е.

разрешающая способность тем больше, чем выше порядок спектра т и число щелей г. Работа со спектрами высоких порядков затрудняется их слабостью и наложением спектров, поэтому повышение разрешающей способности делается главным обр. за счет увеличения п. С наиболее совершенными современными решетками возможны измерения до тысячных долей А. Значительное повышение разрешающей способности м. б. достигнуто при почти скользящем падении лучей на решетку; этим воспользовался в последнее время Тибо для получения рентгеновских спектров от простой стеклянной решетки при отражении. Если придать углублениям штрихов на диффракционной решетке некоторый угол относительно плоскости решетки, то при известных условиях получается чрезвычайное усиление спектра какого-нибудь одного порядка; такой наклон получается применением резцов специальной формы. Диффракционные решетки такого типа (эшелетт Вуда) пе получили, однако, распространения в силу практических трудностей. Спектры чрезвычайно высоких порядков используются в иитерфе-репционных спектроскопах.

Диффракционные решетки с различными штриховками (прямой, круговой) изредка применялись еще с 18 века для получения цветовой игры на пуговицах и других предметах. Вуд применил диффракционную решетку для цветной фотографии, но этот метод не получил распространения.

Лит.: Аркадьев В., Диффракции Френеля, Ж >, 1912, т. 44, фпзич. отд., вып. 4: К а л а ш н и-к о в А., Диффракция Гуи-Зоммерфельда, <Ж , 1912, т. 44, физич. отд., вып. 3; А н д р е е в Н., Электрич. ..олебания и их спектры, М., 1917; М б g 11 ch F., Beugung, Handbuch d. physikalischen Optik, hrsg. von Cehrcke, B. 1, p. 499, Lpz., 1927; В о u a s s e H. et G a r r i ё r e Z., Diflraction, P.. 1923; R i e m a n n ti. F. und Weber II., Die Diffej-ential- u. Integral-gleichungcn der Mechanik und Physik, T. 2, p. 433. Braun.schweig, 1927; Л1 i с h e 1 s о n A. A., Studies in Optics, Chicago, 1927. C. Вавилов.

ДИФФУЗИЯ, происходящий во времени процесс выравнивания концентраций (парциальных давлений) в газе, жидкости или твердом теле, стремящийся к равновесному состоянию одинаковости концентраций. Такое определение Д. относится к системам, состоящим не менее, чем из двух компонентов, но и в однокомпонентном газе тоже может происходить Д., если под Д. понимать уравнивание давления во всех частях газа.

Д. изучалась с начала 19 в. Дальтоном, Бертолле и Гремом, но только Фик в 1855 г. развил количественную теорию Д., показав, что кинетика Д. вполне аналогична кинетике теплопроводности (см.), теория к-рой была развита Фурье. Причиной Д. является наличие градиента концентрации с по направлению X, т. е. . Первый закон Фика

Д.ТЯ массы вещества dm, диффундирующей за время dr через поверхность S, при условии, если градиент концентрации перпендикулярен к S, выразится таким образом:

dm = -I)S

dc , dr.

Знак (-) указывает на то, что dm>0, если

dc г.

- < О, т. е. если с падает с возрастанием ж;

D-коэфф-т Д., измеряемый количеством вещества, диффундирующим за время йт=1

через S = l при градиенте = 1; размерность

[D] = зрд; в абсолютной системе единиц D измеряется в см/ск. Если принять, что D не зависит от с, то из первого получается второй закон Фика:

Sc у-, дс

дг дх

Физически это означает, что изменение с со временем в данном элементе объема системы может происходить только в случае различия градиентов ~ с обеих сторон этого элемента, т. е. только в случае, когда не

дс дс

равно нулю. Когда Const, то=0 и

по (2)1=0.

Наибольший интерес представляет Д. в газах и жидкостях. Д. в твердых телах происходит крайне медленно, хотя Робертс-Аустен интересными опытами и показал, что в прижатых друг к другу концами брусках металлов (например, Аи и РЬ) происходит диффузия (спустя долгое время бруски резались на слои и анализировались).