нейного Д. у., надо найти его частное решение. Если правая часть /(ж) имеет вид е°*р(ж), где р(х)-многочлен, то частное решение ищется в таком же виде: Г=е -(ж), где q(x)-многочлен с неопределенными коэффициентами, к-рые подбираются так, чтобы Y удовлетворял неоднородному уравнению. Общее решение, как указано выше, будет у + Y, где решение однородного ур-ия.

Интегрирование с помощью рядов. Если решение Д. у. не выражается в элементарных ф-иях, можно искать его выражение в виде стененнбго ряда. Это метод особенно часто применяют к линейным Д. у. с неремеиными коэфф-тами для нахождения частных решений. Он состоит в следующем: ищем решение в форме степенного ряда

у = Ао + Ах + А. + ...+ ж +... (9)

с неонределенными коэфф-тами А, А, J.2,.-. Подставляя в Д. у. вместо у ряд (9) и вместо у, у -ряды, получаемые формальным дифференцированием ряда (9), мы должны получить тождество; приравнивая нулю коэффициенты при разных степенях ж, получим систему уравнений для определения А, А, Аг... , при чем некоторые из этих коэффициентов могут остаться неопределенными,-они войдут в решение как произвольные постоянные.

Пример. Рассмотрим Д. у. Бесселя ну. [евого порядка: ху + у + жг/ = 0. Подстав. шя в него вместо у и его производных ряд (9) и ряды, получаемые почленным дифференцированием, и собирая члены при одинаковых степениях ж, получим тождество:

Ai+{1- 2А, + 2А., + Ао) х + {2- ЗА, + + ЗА, + Ai)x+... +[п (п -1) + пА + + А-2]я +... = 0. Отсюда, приравнивая нулю коэфф-ты при различных степенях ж, находим: А = О, 2 = = -5 и вообще А=-- Т. о.,

J.3= J.5 = . . .=a i = 0;

= =---1

* 2*-4 2*-(1-2)=

...Л = (-1Г

-4 с

22W (1.2 ...п)

jIq осталось иеонределенным; полагая Al, найдем частное решение уравнения Бесселя:

у = 1о(.ж) = 1 - -f - .7 + . . .

Это-функция Бесселя 1-го рода (см. Бессе-левы функции).

Система обыкновенных дифференциальных уравнений. Задача ставится так: найти мфунк-ций Уу, if/a, ...,Уп независимого переменного ж, удовлетворяющих п ур-иям, в к-рые входят независимые переменные, искомые ф-ии и их производные. Дифференцируя данные ур-ия несколько раз по ж, мы получаем добавочные Д. у.; из полученной системы можно исключить все искомые функции, кроме одной, и свести, т. о., задачу к интегрированию одного Д. у. (высшего порядка).

Пример. Дана система двух дифференциальных уравнений:

Дифференцируем 1-е уравнение по ж:

из 2-го ур-ия через -2yi, полу-

заменяя

чим:

(линейное Д. у. 3-го порядка с постоянными коэфф-тами). Его общее решение:

г/1=(Сх + СаЖ) е-ЬСзб- Из 1-го ур-ия находим:

-2с2(ж-1) e-fcge- Обратно, всякое Д. у. п-то порядка можно заменить системой Д. у. 1-го порядка введением новых функций. Пусть уравнение имеет вид (1); наряду с у вводим новые функции Vl = У\ Уч = У , , Уп-1 = 2/( >. Тогда данное уравнение примет вид:

К{х,у, У1,2/2,-.., Уп-1, = О

и к нему присоединятся еще п-1 ур-ий:

% = =

dx J dx У2> ) д. Уп-1-

Общее решение системы п Д. у. 1-го порядка

t=/i(2/i,...,2/J, .:,-fn(x,yi,-.Уп) (10)

зависит от п произвольных постоянных; оно имеет вид:

yi=(Piix,Ci,...,CJ,..,y = (р (ж, Ci, ...,CJ; (И) для определения произвольных постоянных д. б. заданы начальные значения искомых ф-ий; при x = Xq должны иметь: У1 = у1,... Уп=Уп (где Жо, 2/?,..., ?уЯ суть заданные числа). Систему решений (11) можно представить в другом виде, разрешая п ур-ий относительно п величин Ci, Сг, Сз, ...,С ; получим: Vl (ж, 2/1,...,2/, )=Ci,..., v, (ж, 2/i,..., г/ ) = (7 . (12) Соотношения (12) называют интегралами системы (10).

Уравнения в полных дифференциалах с 3 переменными. Рассмотрим ур-ия вида

Pdx+Q dy + Rdz = 0, где Р, Q, Д-данные ф-ии от ж, у, z. Если существует интегрирующий м н о лг и-те ль i-iix, у, z), по умножении на который .тевая часть ур-ия стаьювится полным дифференциалом от нек-рой функции и{х, у, г), то ур-ие примет вид du=Q, интеграл его будет, очевидно, и{х, y,z) = С. Оказывается, не всякое ур-ие имеет интегрирующий множитель; для его существования необходимо и достаточно тождествен, выполнение условия:

Р[д- дy) + [-0Х -oz} + W~ aVj = Д. у. с частными производными. Так называется ур-ие, связываюшее искомую ф-ию от нескольких независимых переменных, эти переменные и частные производные от искомой ф-ии. Д. у. с частными производными 1-го порядка с искомой ф-ией z и независимыми переменными хну имеет вид:

/ dz dz\

Р(х,У,,Ш ау)-0.

g-32/x-2/2 = 0.

s + 22/x = 0.

Если производные и входят в 1-й

степени, мы имеем линейное уравнение с частными производными. Оно имеет вид:

(13)

где Р, Q, iJ-заданные ф-ии от х, у, z. Его интегрируют следующим образом. Пищем систему (двух) обыкновенных Д. у.

dx dy dz ....

Р Q R

Как ранее указано (12), она имеет 2 интеграла: и(х,у, z)=Cy, v{x, у, z) = C2. Тогда общее рещение ур-ия (13) примет вид: vf (и), где /-произвольная ф-ия. Т. о., общее рещение Д. у. с частными производными зависит от произвольной ф-ии. Д.71Я ее опреде-.яения д. б. даны начальные усяовия (зад;:.-ча Кощи): при ж= х , z должна обращаться в данную ф-ию fp{y): а именно z = (р{:у).

Пример. Xj + у ly Система (14) есть

ее интегралы: - = Cf, = С,. Общее рещение:

(J-произвольная функция).

Из Д. у. с частными производными 2-го порядка рассмотрим как пример ур-ие колебания струны. Если t обозначает время, ж-расстояние точки струны от одного конца (ж = 0), ж= г-второй конец струны, 0-уклонение точки струны от положения равновесия, а-постоянную, то Д. у. напи-щется так:

dV dx

Для нахождения определенного решения д. б. заданы: 1) граничные условия: 2 = 0, при ж = 0 и при х=1, для всякого t, 2) начальные условия: мы должны при < = 0 иметь:

Z = fix),-=fi{x) (где / и /i-заданные ф-ии).

Ищем частное решение в виде z = XT, где X зависит только от х, Т-только от t. Подставляя это выражение для z в уравнение (15), находим:

т X аТ X

Так как левая часть зависит только от t, а правая-только от х, то последнее равенство возможно лишь, если обе части равны одной и той же постоянной -к; получаем:

X + кХ = 0; Т + акТ=0. Для 1-го уравнения имеем частные решения: X=coskx; X=sin кх. Используя граничные условия, имеем Х(0) = О, Х(1) = 0; решение cos кх не подходит, а решение sin кх удовлетворяет условиям лишь при /с = О, + ,

+ -у ,+ ,... Отбрасывая нуль и отрицательные значенрш, получим численное множество решений для Т вида:

nnat

nnai

И бесчисленное НИИ для z:

алЬ . пх

COS -J- sm -J-

мнолсество частных реше-

cos -j- sm -j-

nant . пях cos- у Sin у

ал1 . пх . 2ant . 2лх

sm J sm-y , sin sm ,...

. nant . nnx

Sin sin у ,...

Решение данного Д. у. ищем в виде бесконечной суммы частных решений с постоянными коэфф-тами а. , Ь :

п = оо

z{x,t)-= 2 к COS+ Sin -f) sin .(16) n = l

Для определения постоянных a , воспользуемся начальными условиями; полагая в (16) t = О, получим:

П=оо

а Sin-у-=/(ж),

т. е. определятся как коэффициенты раз;1о-жения данной ф-ии /(ж) в тригонометрический ряд Фурье (см. Гармопический анализ). Далее, дифференцируя (16) по t и полагая = О, имеем:

п=оо

2ппа , . ппх x / \ у b sm =/,(ж),

откуда Ь определятся через коэфф-ты разложения /(ж) в ряд Фурье.

Лит.: Ф и л л и II с Г.. Дифференц. ур-ия, пер. с англ., М.-Л.,1 926; Т а м а р к и н Я. Д. и Смирнов в. И., Курс высшей математики для техников и физиков, т. 2, .Л., 1 926; С т е к л о в В. А., Основы теории интегрирования обыкиовен. дифференц. ур-ий. М.-Л.. 1927; Forsyth А. R., Lehrbuch d. DiHerential-gleichungen, 2 Aufl., Brschw., 1923. B. Степанов.

ДИФФРАКЦИЯ, явления, наблюдаемые при огибании волнами встречных препятствий. Чаще всего при этом подразумевают нарушение прямолинейности распространения возбуждения и интерференционные процессы, сопровождающие огибание. Строго говоря, Д. всегда сопутствует распространению волн (являясь, в сущности, синонимом этого распространения), но в непосредственно явной и отчетливой форме она обнаруживается для любых волн в том случае, когда размеры огибаемых препятствий соизмеримы с длиной волны или значительно меньше последней. Обычные звуковые, сейсмические и радиотелеграфные волны вполне удовлетворяют этому условию, и потому нарушение прямолинейности распространения и другие диффракционные явления здесь привычны. Большое значение-теоретическое и практическое-Д. имеет для оптики, ибо наличие диффракцион. явлений здесь-основной довод в пользу волновой теории света, главное средство для изучения свойств световых волн во всех частях спектра и одновременно - непреодолимое препятствие, ставящее предел разрешающей способности оптич. приборов (см. Оптические приборы. Микроскоп). Д. света легко наблюдать при рассматривании уда.яенного малого источника света сквозь очень узкие отверстия и сетки, при прохождении света около малых препятствий. Нек-рые метеорологич. явления (радуга, круги вокруг солнца и луны)- диффракционного нроисхолодения. Д. объясняется и рассеяние света мутными средами. При наблюдении с белым светом в результате Д. и интерференции происходит разложение света в спектр, благодаря чему возникают различные хроматические картины.

В монохроматич. свете Д. обнаруживается чередующимися темньвми и светлыми интерференционными полосами, кругами или пятнами. При некоторых условиях Д. сопровождается также поляризационными явлениями. Д. существует для волн любой длины, начиная от длинных электромагнитных волн и кончая жесткими у-лучами.

Характер диффракционных картин зависит от формы препятствий или отверстий, их размеров, способов наб.аюдеиия, состава падающего света и других условий. На вклад-пом листе (см. диффракционные картины 1 и 2, но фотографиям А. Г. Калашникова) виден результат прохождения параллельных видимых лучей через широкое отверстие в экране PQ и через очень узкое (тысячные доли мм). Свет скользил по фотографической пластинке, поставленной L к экрану, и запечатлевал свой след на пластинке. Для широкого отверстия практически остаются в силе законы геометрич. о птики-о б-разуется правильная геометрич.тень; для узкого отверстия эти законы резко нарушаются, свет через отверстие идет по всем направлениям, но по нек-рым-преимущественно. Если бы отверстие было сужено до десятитысячных долей мм и далее, то расиространение света стало бы равномерн. по полушару. На вкл. л., 3, видна сложная диффракционная картина при прохождении через клиновидную щель, контуры которой отмечены пунктиром. На вкл. л., 4, приведена фотография диффракционной картины, по-. хучающейся при прохождении света через малое круг.яое отверстие; на вкл. л.,5,-фотография тени конского волоса; на вкл. л., 6,- фютография тени маленького диска. В отличие от 1 и 2, фотографии 3-5 (по В. К. Аркадьеву) сделаны на большом расстоянии от огибаемого тела и с пластинкой, расположенной J к световому пучку.

Точная теория явлений Д. даже для са-агых простых случаев-одна из наиболее трудных, в математич. отношении, задач физической оптики. Существует несколько методов решения диффракционных задач. Наиболее прост и нагляден метод Френеля; он основан на принципе Гюйгенса, дополнен-иом принципом интерференции (см.). Трудность задачи в том, что волновая функция распределена по всему окружающему объему, и первый способ ее упрощения состоит в том, чтобы свести объемную функцию к функции, распределенной по поверхности. Это и достигается в элементарной прибли-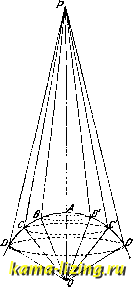

Фиг. 1.

лсенной форме принципом Гюйгенса. Действие светящейся точки О на данную точку Р (фиг. 1) заменяется действием поверхности волновой сферы ADD. Френель разбивает эту сферу на зоны (зоны Гюйгенса-Френеля) след. образом. Из точки Р радиусами

i РА + РА + \Х, РА+\Х, ... проводятся сферы, рассекающие сферу ADD на шаровые зоны. Последующая зона, в среднем, имеет фазу волновой функции, противоположную предыдущей, и действие соседних зон (при отсутствии препятствий между О и Р) приблизительно нейтрализуется благодаря интерференции. Простой расчет показывает, что действие свободной, незакрытой волны на Р сводится к действию половины центральной зоны, что и соответствует в первом приближении прямолинейному распространению света. Если нек-рые зоны полностью или частью закрыты каким-либо экраном, то, меняя положение точки Р, будем получать в ней попеременно то усиле-рию то ослабление света, что соответствует полосам, пятнам, ко.тьцам. Метод Френеля неточен, он дает постоянную ошибку в фазе на (что не сказывается, впрочем, на интенсивности, единственно доступной опыту величине) и, кроме того, связан с другими упрощающими,произвольными предположениями относительно действия зон.Тем не менее для большинства простых диффракционных задач этот метод вполне пригоден и дает хорошее совпадение с опытными данными.

Различают два типа задач: 1) Д. сферич. волны (Д. Френеля) и 2) Д. плоской волны, наблюдаемой в параллельных лучах, например при помощи зрительной трубы, наведенной на бесконечность (Д. Фраунгофера). Решение задач первого типа значительно сложнее, чем второго. Окончательное выражение Д.ЯЯ интенсивности J в некоторой точке диффракционной картины имеет вид J =A\C-\-S), где А-постоянная величина, а С и /S выражаются через т. н. интегралы Френеля:

= J* cos и du; ?? = J* sin du.

Таблицы Д.ЯЯ этих интегралов имеются во всех подробных изложениях диффракционных явлений. Легко видеть, что

dS + drj= du,

т. е. и может считаться как элемент дуги нек-рой кривой, отнесенной к осям Тангенс угла наклонения кривой к оси I, т. е.

tg(r)=tg {~и),

т. е. т= м, радиус кривизны кривой

()==:, т. е. обратно пропорционален длине дуги. Кривая асимптотически завивается вокруг точек (-f А ,-}-) и (-\,-,

т. е. является спиралью (спираль Корню, фиг. 2). Спираль Корню служит весьма по.т1езной геометрической интерпретацией интегралов Френеля, которая позволяет очень быстро представить общий характер диффракционной картины.