отверстие шпинделя Р =

2лМ t-f,

может быть

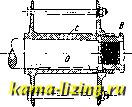Фиг. 3.

сделана весьма значительной путем уменьшения разницы ходов нарезок гайки.

Другой пример дифференциальной гайки изображен на фиг. 3; гайка В, к-рая снабжена наружной и внутренней резьбами с различным шагом, навинчивается на винт А и одновременно ввинчивается во вт-лку С; переме-шение втулки С относительно конуса В за один оборот гайки равно разности ходов внутренней и внешней нарезок. Гайка показана в применении ко втулке воздушного винта авиац. двигателя АНЮ Ленинградской лаборатории двига-те.тей; она позволяет не только натягивать втулку на конус при надевании винта, но также и стягивать ее при снятии последнего. Интересный пример Д. м. изображен на фиг. 4. Этот механизм служит для преобразования быстрого вращательного двилсения в медленное поступательное. Винты А и В приводятся во вращение от шесте] )-як Е в различном направлении и со слех-ка отличающимися угловыми скоростями и а>2; червячное колесо G зацепляется одновременно с обоими винтами и вследствие разницы их угловых скоростей катится медленно по винту с более медленным вращением. Обозначая скорость вращения зубчатки Е через п (об/мин.), числа зубцов шестерен Е, F я В-через z, гя z, шаг винтов-через h {мм), получим скорость движения ползуна Я:

= MMiMun..

Насколько медленное двил-сение можно получить посредством этого Д. м., видно из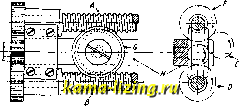

Фиг. 4.

следующего примера: пусть п = 100 об/мин., 1=20, Z2=100, z = lQi и мм, тогда

V=0,297 MMJMUu.

Дифференциальный ворот. Канат в этих воротах (фиг. 5) навернут в противоположных направлениях на барабан, имеющий два различных диаметра В я d. При вращении один конец каната сматывается, а другой наматывается на барабан. За один оборот блок перемещается вертикально на величину

h = l{B-d).

Называя скорость точки М через v, а угловую скорость вала через со, найдем: D-d

Пренебрегая трением, получаем подъемную СИ.11У ворота

При вращении вала блок М движется не только вертикально, но ташке и в горизонтальном направлении в ту яп.я другую сторону. Хотя за один оборот вала длина наматываемой и сматываемой веревки на диаметрах В я d различна, все же в горизонтальном направлении блок переместится только на расстояние одного витка, равное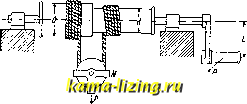

Фиг. 5.

диаметру веревки, и благодаря этому ветви веревки, проходящей через блок, все время будут параллельны между собой.

.Лит.: 3 е р н о в Д. С, Приилтадная механика, Л., 1925; Столяров Я., Теория механизмов, Харьков, 1926; Делоне Ы., Лекции по практическойг механике, СПБ, 1901. И. Бобарыков.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ,соотношения, связывающие независимые переменные, искомые функции и их производные различных порядков.

Общий вид Д. у. м-го порядка:

F{x,y,y,y ,...,y(n))0. (1)

Порядок высшей производной, входящей в ур-ие, называется п о р я д к о м Д. у. Р е-шить (интегрировать) Д. у. значит найти функцию y = t{x), обладающую следующим свойством: если в ур-ие (1) подставить fix) вместо у, f\x) вместо у, fx) вместо то уравнение (1) обратится в тон%-дество. Такая ф-ия называется решением (интегралом) Д. у. Кривая, определяемая ур-ием y = f(x), называется интегральной кривой. Общее решение Д. у. есть решение, содержащее произвольные постоянные в числе, равном порядку ур-ия; т. о., для Д. у. п-го порядка общее решение имеет вид: y=-f{x, Ci, Сг,CJ, где С, .....Си-произвольные постоянные. Геометрически мы имеем семейство кривых, зависящее от п параметров. Всякое решение, которое по-.тучается из общего, если произвольным постоянным даны определенные численные значения, называется частным. Частное решение вполне определяется (т. е. численные значения произвольных постоянных можно вычислить), если заданы начальные условия. Эти условия для обыкновенного Д. у. таковы: ищется такое решение у, которое при данном численном значении независимого переменного ж = Жо принимает значение Уо, я его производные до (n-l)-ro порядка, у, у ,у(~), принимают соответствен, значения Уо, Уо , 2/Г~-

Пример. Д. у. движения тяжелого тела

по вертикал:и: = - gr, где < (независимое переменное)-время, ж (искомая ф-ия от t)-

высота тела в момент времени t, д-постоянное ускорение силы тяжести. Общее решение:

Для определения Ci и надо задать для начального момента t = О высоту тела Xq и начальное значение производной , т. е. начальную скорость Vq. Для данных Жц и получим: X = - Y -\-vt + х. Решение Д. у., не получаемого из общего ни при каких значениях произвольных постоянных, называется особым.

Методы интегрирования Д. у. 1-го порядка вида:

Fix, у, у) = О, (Г)

у= fix, у). (2)

Общее решение до.тжно содерлсать одну произвольную постоянную.

Разделение переменных. Предположим, что fix, у) в ур-ии (2) есть произведение ф-ии только от х на ф-ию от одного у, т. е. fix,y)= Mix) Niy). Пишем ур-ие при помощи дифференциалов dy= Mix)-Niy)-dx; разделяем переменные:

dy N(y)

= Mix) dx.

Беря неопределепные интегралы от обеих частей, находим:

Sy-lMix)dx + C. (3)

Соотношение (3) дает возможность выразить у в ф-ии ж и С, т. е. дает общее решение.

Пример: Разделяя перемен-

ные: у dy= -X dx, находим общее решение: ж2 -Ь г/2 = С.

Интегральные кривые образуют семейство концентрических кругов с центром в начале координат.

Однородное Д. у. 1-го порядка можно привести к виду:

Для интегрирования вводим новую искомую функцию V ири иомощи соотношения:

= V, или у = VX. Отсюда dy = vdx-\-x dv.

Вставляя полученные выражения у и dy в данное Д. у., освобожденное от знаменателя dx, получим: v dx + xdv = fiv) dx, или xdv= [fiv) - v] dx, или, наконец,

dv dx

Переменные разделены, и общее решение будет:

стоянные). Если в частности Q=0, то имеем линейное дифференциальн. уравнение вида:

В иолученном результате надо еще заменить V через i

Линейное Д. у. 1-го порядка. Так на-

тт dy

зьшается Д. у., в которое у и входят в 1-й степени. Оно м. б. написано в виде:

+ Р-2/=д, (4)

где Р и Q-ф-ии от ж (или, в частности, по-

+ Р-2/ = 0,

которое решается разделением переменных:

= - Р dx; In ?/ = - JP dx + С.

Взяв произвольное постоянное в виде С = = In Ci и потенцируя, получим окончательное выражение общего решения:

Для интегрирования ур-ия вида (4), при Q тождественно не равном О, полагаем искомую ф-ию у равной произведению двух ф-ий от ж, напр., у= и V. Подставляя в ур-ие (4), имеем: -{-(и-ЬР v)=Q. Подбираем функцию V так, чтобы выражение в скобках равнялось тождественно нулю: v+Pv zO, отку-

-SPdx , SPdx

да г; = е ; тогда получим: и = Qe , л S Pdx

u = jQ-e dx + С и, наконец, общее решение:

ye-Plc+jQe-JP-dxl

Интегрирующий множитель. Всякое Д. у. 1-го порядка может быть представлено в виде:

Mix, у) dx + (ж, у) dy = 0. (5)

Левая часть ур-ия (5) будет полным дифференциалом, если существует такая функция и ix, у), что ее полный дифференциал du = = Mix,y) dx+Nix,y) dy. Это значит, что

Ж = 1 , JV = 1 , а для выполнения этих равенств, как доказьшается в дифференциальном исчислении, необходимо и достаточно, чтобы имело место тождество:

дм dN .р.

Wdx-

В этом случае ур-ие (5) принимает вид: dw = О,

и его интеграл будет uix,y)== С. При выполнении условия (6) Д. у. (5) интегрируется так: считаем 2/ постоянным idy = 0) и интегрируем полученное равенство dtt = = Ж(ж, у) dx по ж; получаем:

u=jMix,y) dx+(piy).

Мы написали qiiy) вместо постоян. интегрирования, т. к. она может зависеть от у, принятого за постоянное. Для определения (piy) дифференцируем полученное равенство по у

ди -.т

и вследствие равенства = получаем:

4>iy)-N-Sdx,

откуда интегрированием по г/найдем q>iy), а следовательно, и и. Если условие (6) не выполнено, оказывается все же возможным найти такую функцию / (ж, у), по умножении на которую уравнения (5) левая часть его становится полным дифференциалом. Такая функция называется интегрирукзщим множителем.

Пример. Д. у. у dx - ix + y)dy== 0; левая часть его не является полным дифференциалом. Уравнение имеет интегрирующий

множитель J; умножив на него, получим:

У yi If г у > у2 ,

d м эту; 1.

ду ~ дх у

условие (6) выполнено. Имеем:

дифференцируем по у и приравниваем результат N:

X , ,у \ х + у

--i + 4>i:y)-~yi-, откуда fp{y) = - у ; ?(?/) = -1п у. Интеграл искомого уравнения есть и = - \п у + С.

Д. у, высших порядков, д. у. 2-го порядка. Из Д. у. 2-го порядка только весьма немногие типы имеют решения, выражаемые с помощью знака неопределеного интеграла над данными функциями (знака квадратуры). Рассмотрим нек-рые из этих типов.

а) Д. у. не содержит у \ оно имеет вид: Интегрируя 2 раза, получаем общее решение:

Сюда относится рассмотренное нами ур-ие: dx

б) Д. у. не содержит у; оно имеет вид:

-f(x

dx~l Г dx)

Вводим вспомогательн. переменное Р = ; уравнение будет 1-го порядка и примет вид:

Если найдем его общее решение р = 95(37,С), то имеем:

i-Pix, с,),

откуда у = J <р(х, Ci) dx + С-

в) Д. у. не содержит х; оно имеет вид:

dx lydx) Вводим новое переменное Р = и выра-

;каем следующим образом:

d*y . dp

dx dx~ dy dx dy

Получаем Д. у. 1-го порядхса: = /(2/,р).

Проинтегрировав его, получим р=у>(у, Cj), или - = V(2/> Ci). Разделяя переменные и интегрируя, получаем общее решение:

Л и н е й и ы е Д. у. п-г о порядка вида:

Pi2/< -i>-f ... 4-Рп-гУ + РпУ= Кх), (7)

где Pi, Ра. Рп, вообще говоря, ф-ии от х; мы будем рассматривать, гл. обр., случай, когда все они-постоянные; тогда имеем ли-

нейное Д. у. с постоянными коэффициентами. Если f{x) = О, то Д. у. называется однородным (или без правой части), в противном случае неоднород-н ы м. Для линейного однородного Д. у. справедливы теоремы: если г/ есть решение уравнения, то Cyi (С-постоянное) тоже- решение; если у и у2-решения, то Ух + у, тоже-решение. Поэтому для нахождения общего решения однородн. линейного Д. у. достаточно найти те частных решений (удовлетворяющих условию т. н. линейной не! зависимости) уу, У2,.--,у ; тогда общее решение напишется так:

у=С,У1 + С2У-г + ...+С у . (8) Для неоднородного уравнения доказывается теорема: если известно частное решение Y неоднородного Д. у. и общее решение (8) соответствующего однородного ур-ия (т. е. получаемого из уравнения (7) заменой /(ж) нулем), то общее решение неоднородн. уравнения есть: у + Y. Переходим к уравнению однородному линейному с постоянными коэффициентами. Наша задача свелась к нахождению п частных решений. Ищем их в форме: у=ё(геще неизвестное постоянное) . Имеем: у = ге у = ге* ,..., t/(n)=r e*. Подставляя в левую часть уравнения (7) эти значения у, у , yW, получим выражение: н + ,. . г + РпУ, приравни-

вая это выражение О и замечая, что е*ФО, получаем для г алгебраическое ур-ие те-й степени (характеристическое ур-ие): r + Pir -+... + Рп-1Г + Рп=0. Это ур-ие имеет п корней: г, Га, ...,г . Если они различны, получаем те различных (линейно независимых) частных решений: e* i*, е* * ,eV, и общее решение напишется в виде: у=Су е1 -f Саб- + ... + С fV. В случае, если какой-нибудь корень, пусть fl, имеет кратность больше 1, например 3, этому корню соответствуют три частных решения: ei, хёг и a;e i*. Если в числе корней характеристич. уравнения есть мнимые сопряженные корни: a + fiiiia - i, то им

соответствуют частные решения у = и 2/2= е°~*. Пользуясь формулой

е* = cos x + i sin х и беря вместо у и у2 их линейные комбина-

ции i/i =

У1+Уг

2/2 =

Vi - у г

2 2i

ствительных частных решения:

получим два дей-

2/1 = cos,

у.2 = е sin fix.

Пример, у + у -г у = 0. Характеристическое ур-ие: r-fr-f 1=0; его корни:

2 2- 2 2

Частные решения:

У1 = е\ 2+2 7*-; 2/2= е\ 2 2 V; или же:

2/i = e-%os,,= e-%in4=*-Общее решение:

= e-(c,cos->-b Casing)

Чтобы получить решение неоднородного ли-