дЕх 1?1 = о-

= 0.

(IF) (HI)

dx dy-- a)

Здесь £-диэлектрический коэфф. среды, ц- проницаемость, с-скорость света в пустоте. Как показал Герц, эти ур-ия можно интегрировать при помощи вектора Герца JP, удовлетворяющего дифференциальному ур-ию:

St V .

ИЛИ в координатах:

Тогда

J/s = rot rot J*,

V - ----Yen

(3) (4)

скорость раснространения света в данной среде. Если электромагнитное поле создается Д., заряд к-рого колеблется по какому-либо закону, то вектор Герца будет иметь постоянное направление, параллельное оси момента Д. Модуль этого вектора Л м. б. выранеен в этом случае при помощи ф-лы

в которой /-произвольная функция, ненре-рывная вместе с первыми двумя производными по координатам и по времени, а г-расстояние от центра диполя. Получаемый таким образом интеграл дает сферическую волну, распространяющуюся из начала координат со скоростью V.

Вид функции / очевидно будет определяться характером двилсения зарядов в колеблющемся Д. Временно оставляя вид функции / неопределенным, находят соста-вляюпще магнитного и электрич. векторов. Если момент Д. параллелен 0Z, то уравнения (3), (4) и (6) дают для проекций Е и Н выражения:

Я,= 0

Выражения (7), так же как и (6), обращаются в бесконечность в начале координат. Следовательно, найденные рещения не дают физически верной картины поля в непосредственной близости к Д.

Вьщелив эту часть, рассмотрим ур-ия (7) во всем остальном пространстве. Слагаемые

вьфажений (7)-величии.! разного порядка относительно перемешгой г. На малых расстояниях все члены ничтолшо малы по сравнению с первыми, зависящими от минимальной степени расстояния. Кроме того, при малом г можно считать, что

В виду этого в части, близкой к Д., ур-ия (7) принимают такой вид:

Чтобы определить вид функции /, сравним электрическ. ноле, определяемое выражениями (7), со статич. полем Д. Это сравнение приводит к необходимости выбрать ф-ию / таким обр., чтобы вбл1-1зи начала координат она переходила в переменный момент Д.:

= (9)

Рассмотрим теперь поле вдали от Д. в волновой зоне (см.). При достаточно больщом г, в выражениях (7) можно пренебречь всеми членами за исключением последних, содержащих г в максимальной степени. Введем сферич. координаты:

= sin д- cos 9?, = sin & sin (р, = cos &, (10)

где S-зенитное расстояние, а у-долгота сферической системы координат; тогда

еЕх = / (f-1) cos <р sin & cos eE,j = 1/ {t - 0 sin sin cos d-eE,= -r{t-l)sm-.9

x=-ifr(*-0sin?.sin

Я = -r(t- cos (p sin &

у cvr \ V/ Я,= 0

Из этих ф-л видно, что Е VL Н совпадают по фазе. Обычным образом можно найти, что

Е 1 Н, Е ±г II Н А г. (И)

Следовательно, в волновой зоне, на поверхности сферич. волны, линии магаитного поля совпадают с параллелями, а линии электрического поля-с меридианами. Абсолютная величина векторов Е и И определяется уравнениями:

(7 )

(12)

11 = \/е; + е1 + е1 = -\/ sin &] I я I = уяи-я + Й = - Э

Из ур-ия (12) видно, что вектор Пойнтинга/S (плотности энергии) направлен по радиусу сферы; по абсолютной величине он равен:

J (t-)sin&, (13)

\S\ = £\E\.\n\ =

4л I I I I 4svr

Энергия, которая излучается колеблющимся диполем за время t, определяется как

поток вектора энергии через всю поверхность сферы за время t:

2Л Л t

St = Jd<pfd&J\S\rsin &dt =

(14)

в случае гармонически колеблющегося Д.

M = ql sin -= f;

(15)

излучаемая им за период Т энер гая, на основании ур-ия (14),

St =

16 лдЧ

(16)

3 е.

где k=vT-длина излучаемой Д. электромагнитной волны.

Лит.: Хвольсон О. Д., Курс физики, 2 изд., т. стр. 339-405, Берлин, 1923; Эйхенвальд Л. А., Теорет1гч. физика, ч. 1-Теория поля, М.-Л., 1927; Hertz Н., Untersuchungen uber die Ausbrei-tung der elektr. Kraft, Lpz., 1914; Abraham M., Theorie der Elektrizitat, B. 1, 7 Aufl., Lpz., 1923; Cohn E., Das elektroraagnetische Feld, 2 Auflage, Berlin, 1927. K. Тводорчин.

Диполь мол окулярный. Всякая частица вещества всегда состоит из нек-рого числа разноименных электрическ. зарядов. Если в сумме эти заряды дают либо положительный либо отрицательный заряд, то имеется наэлектризованная частица, называемая ионом. Если же частица, напр., молекула, электронейтральна, то центры масс всех положительных и всех отрицательных зарядов могут не совпадать. Если расстояние между этими центрами равно d (п л е ч о Д.), а сумма положительных зарядов (равная сумме отрицательных) равна е, то / = ed

будет величиной электрич. дипольного момента. Дебай и Дж. Дж. Томсон предложили разделять молекулы на дипольные, или полярные, обладающие б. или м. значительным готовым дипольным моментом, т. е. Д. в отсутствии внешнего электрич. поля, и на неполярные (для них /=0). К полярным относятся молекулы, построенные несимметрично из химически активных (а) и неактивньгх (6) групп по схеме [а-Ь]: ъ ь

N--H \н

органич. вещества, содержащие углеводородную цень или ядро, к одной стороне которых присоединены полярные группы -NHg,-СО-ОН,-ОН,-NO2 и др., напр.:

aba b

NH.-С.Н анилин

СООН-CHCH.CHjCH, . п-валериановая к-та

Такие вещества имеют весьма высокую диэлектрическую постоянную (е), напр.:

но = cj-isOH = 22 , резко убывающую с температурой (Т): молярная поляризация

где М-молекулярный вес, В-плотность, а а и Ъ-постоянные, при чем

{N - число Авогадро, fe= - постоянная Больцмана и /л-момент Д.); при этом а за-

висит от возможного смещения зарядов в молекуле иод действием внешнего электрич. поля. Очевидно, что величину момента Д. можно определить из экспериментальных данных для изменения диэлектрич. постоянной с Т. Т. о., получены значения: /NH3 = 1.53 10-18, сн,оя = 1.64 . 10-1 , /нс1 = 2,15. 10-1 .

Порядок этих величин совпадает с вычисленными значениями: если принять заряд электрона 6=4,77-10 (в электростатических абсолютных единицах), а диаметр молекулы d 10~ см, T0jws5 101*. У неполярных веществ 4=0 или близко к 0. Их диэлектрич. постоянная практически не изменяется с Т (Ъ=0). В молекулах таких веществ или нет вовсе полярных групп (углеводороды) или полярные группы расположены симметрично и не образуют Д. Так, для окиси углерода о =0,12-10-18; для CH3NO2 (полярно) е=56, для симметричного же тетранитроме-тана C(N02)4 е=2,1, т. е. имеет то же значение, что для всех неполярных углеводородов (е2). Внешние электрич. поля, сме-хцая заряды в молекуле ( поляризуя молекулу), увеличивают момент Д. или создают его, когда он ранее отсутствовал. В первом приближении Д. иногда можно считать жесткими, недеформирующимися под действием внешнего поля.

Лит.: D е b у е Р., Physikalische Ztschr. , Lpz., 1912, В. 13, p. 97; Jon а М., ibid., 1919, В. 20, p. 19; Handb. d. Radiologic, hrsg. v. Er. Marx, B. 6, p. 605-668, Lpz., 1925; Thomson J., Philosoph. Mag. , L., 1914, 28, p. 757;- P a u 11 W., Ztsclir. f. Physik , В., 1921, В. 6, p. 319. П. Ребиндер.

ДИРЕКТРИСА кривой 2-го порядка определяется как поляра фокуса (см. Конические сечения). Для эллипса, с канонич. ур-ием

4- 5=1, Д.-прямые, выражающиеся уравнениями: ж = ± (где е-эксцентриситет эл-липса= ~ < iV Для гиперболы, с ур-ием - 2 = 1> Д- суть прямые ж = ± - (е-эксцентриситет гиперболы = -- > lj. Для параболы, с уравнением у=2рх, Д. есть прямая ж= - i (см. фиг.). Д. круга есть бесконечно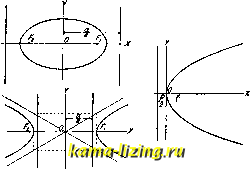

удаленная прямая. Д. обладает следующим свойством: для всякого конич. сечения отношение расстояния любой его точки до фокуса к расстоянию ее до соответствующей Д. есть величина постоянная (равная эксцентриситету кривой), в. Степанов.

ДИРИЖАБЛЬ, управляемый аэростат (воздушный корабль, воздушное судно) - воздухоплавательный аппарат легче воздуха, поддерживаемый в нем подъемною силою газа, заключенного в корпусе Д. Газами для наполнения диринеабля служат обычно: водород и гелий (см. Газ для воздухопла-ватш и Гелий).

Общее описание. Основная часть всякого Д., корпус, имеет удлинен, форму, тупую па носу и более заостренную к корме, что де.дается для лучшего обтекания Д. воздухом и уменьшения лобового сопротивления. На кормовой части корпуса располагается оперение, горизонтальное и вертикальное, состоящее из неподвижно распололшн-ных, обычно крест-на-крест, горизонтальн. и вертикальных поверхностей-стабилизаторов и килей, заканчивающихся (ближе к корме) подвижными рулевыми поверхностями: горизонтальными рулями высоты и.ти

служащую ходом сообщения, а таклсе помещением для горючего, балласта и снарялсе-ния. Эта балка своею жесткостью препятствует деформации оболочки и воспринимает горизонтальные составляющие напря-лсений в подвеске. Неизменяемость внешней формы в мягком и полужестком Д. во время полета, несмотря на сопротивление воздуха, достигается тем, что газ находится в оболочке под некоторым избыточным давлением (сверхдавление), которое постоянно поддерживается находящимися внутри оболочки баллонетами для воздуха (см. Баллонет). В жестком дирижабле нет надобности поддер-лсивать сверхдавление, так как неизменяемость внешней формы обеспечивается жестким каркасом. По кубатуре дирижабли бывают от 1000 до IWOOO и выше.

Д. мягкой системы. Эти Д. обычно имеют небольшой объем: 1 ООО-10 ООО м. На фиг. 1 изображен Д. мягкой системы: к icopnycy-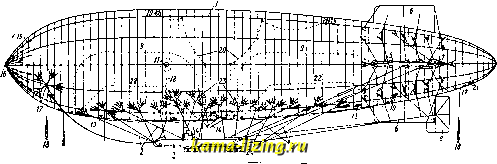

Фиг. 1.

глубины и вертикальными рулями направления. К нижней части корпуса (непосредственно или при помощи строп) прикрепляют одну или несколько гондол, в к-рых располагаются команда и пассалсиры, моторы, снаряжение и пр. В настоящее время строят три системы Д.: 1) мягкую, 2) по.яужест-кую и 3) жесткую. В мягкой системе корпус, изготовленный из материи, служит вместе с тем и оболочкой для газа; в жесткой-корпус образует лсесткое сооружение из дуралю-миниевых, стальных или деревянных балок, обтянутых снаружи материей, а газ помещается внутри корпуса в особых газовых мешках, обычно из бодрюшированпой ткани (см. Бодрюш); полужесткая система отличается от мягкой лишь тем, что в нилсней, килевой части оболочка имеет шарнирную балку из стальных или дуралюминиевых труб, проходящую вдоль всего корпуса и

оболочке 1, при помощи строп 2, подвешена гондола 3 с винтомоторной установкой 4. На корме оболочки расположено оперение: горизонтальные 5 и вертикальные 6 неподвижные планы с прикреп.тенными к ним при помощи шарниров р у .т я м и высоты 7 и направления 8. Внутри оболочки находятся баллонеты 9 для воздуха. По оболочке расположены клапан ы, к-рые служат для выпуска части газа из оболочки; они м. б.: а) автоматические предохранительные 10, открывающиеся при чрезмерном повышении сверхдавления газа, и б) управляемые 11 для маневрирования или спуска Д. Предохранительные клапаны помещают обыкновенно в нилшей части оболочки, ближе к корме, во избежание соприкосновения выходящего газа с выхлопными трубами моторов; управляемые же клапаны располагаются наверху или сбоку в передней части Д. и открываются при помощи клапанной веревки 12, проходящей внутри оболочки. Клапаны 13 служат для выпуска воздуха из баллонетов. Воздух поступает из вентилятора а (фиг. 2) в баллонет по шлангу б. На случай отказа в работе вентиляторного мотора, устраивается иногда матерчатый каркасированный открытый снизу шланг - у л а в л и в а т е .я ь 14 (фиг. 1), помещаемый сзади винта, при вращении которого в него попадает струя воздуха. В Д. системы Парсеваля на.яичие двух баллонетов и специальных клапанов д.ля распределения между ними подаваемого воздуха позволяет пользоваться баллонетами и для управления Д. в вертикальной плоскости: для подъема задний баллонет наполняется