ния (34) и угол из ур-ия (33), получим:

h = 2 / ctg <Р

gCysS cos<р + 1л Угловая скорость вращения самолета по образующему цилиндру будет:

V COS &

Мертвая петля. Правильн. мертвая петля должна производиться в одной вертикальной плоскости без какого бы то ни было скольжения на крыло; поэтому в данном случае общие дифференциальные уравнения движения, принимая v =0, р=0, г=0, 9=0, У=0, L=0, N=0, будут:

-i,<7 = Srcos + Z

(35)

Здесь Z, Z и М-силы и момент, вызванные только воздушным сопротивлением. Интегрирование этих ур-ий не представляется возмонсным, и их решение мы можем найти только приближенно, делая определенные предпололения и производя последовательно построения для положения аэроплана от одной точки к другой. Воздушные силы могут быть найдены исследованием в аэродинамич. лаборатории, при чем компоненты этих сил по оси X и по оси Z находятся обычным путем, момент же тангажа М находится для различных отклонений руля высоты. Есчи обозначим через I расстояние от центра тяжести аэроплана до центра давления горизонтального оперения и через момент горизонтального оперения, то уравнения (35) примут вид:

= ад + & cos & + dt~ В

CtQSv

т C qSv

(обозначения Cf и C,j см. Аэродинамика). Построение траектории мертвой петли м. б. сделано при различных предположениях, как то: выдерживание постоянной перегрузки, выдерливание постоянного угла атаки, выдерживание постоянного угла руля высоты и т. п. Вычисления траектории мертвой петли ц всех сопутствующих ей элементов двшкения для отдельных аэропланов показали, что они сходятся довольно близко с наблюденными на практике величинами. Скорость на нетле уменьшается до наивысшей точки петли, после которой она снова увеличивается; углы атаки вначале быстро увеличиваются, йотом остаются нек-рое время постоянными почти до вершины петли, к самой вершине опять уменьшаются. На фиг. 16 дана примерная траектория петли. Перегрузки, получаемые на петле, зависят от радиуса кривизны петли, т. е. от той резкости, с которой эта петля производится. Истребители с большим запасом мощности, делающие петли со сравнительно малым радиусом, получают большие перегрузки, чем более тяжелые машины. На фиг. 16 указаны как величины перегрузок п, вычи-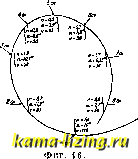

сленных теоретически, так и углы атаки а и скорости V. Опытные исследования показали, что обычная мертвая петля, сделанная не особенно резко, дает наибольшую перегрузку порядка 3; при узких же петлях перегрузка молсет дойти до 6.

Штопор. Штопор является одной из фигур полета аэроплана, динамика которой наименее выяснена. Он характеризуется тем, что аэроплан снижается по очень крутой спиральной траектории; так. образом, штопор можно рассматривать как спираль с очень большим наклоном; ц. т. аэроплана в этом случае описывает винтовую линию со сравнительно малым радиусом (часто меньшим размаха крыла) образующего цилиндра. Харак-терн. особенностью штопора является то, что углы атаки, на которых происходит движение, значительно выше

критического. Т. к. аэродинамические силы на таких углах атаки, вследствие срывов струй, не носят закономерного характера, то это уже одно вносит значительные затруднения в исследование штопора. Рассматривая штопор как спираль, мы получим для него следующие элементы:

v cos 1>

угловая скорость ш =---;

время одного витка t = - ;

снижение за один виток h = 2пг tg & -v - i sin

P cos 9 перегрузка n = - = --.

Вследствие несимметричности движения аэроплана в штопоре, моменты, заставляющие аэроплан вращаться, получаются от действия воздушного потока почти на все главнейшие элементы аэроплана. Т. о. получаются моменты крыльев, моменты оперения, моменты фюзелялса; кроме того, действуют еще и моменты от инерционных сил. Главнейшее действие оказывают моменты кры-.тьев. При штопоре мы сталкиваемся с явлением т. н. авторотации, которая состоит в том, что симметричная поверхность в установившемся потоке под влиянием первоначального импульса входит в установившееся вращательное движение. Авторотация крыльев происходит за счет получающегося несрхмметричного обтекания крыла потоком. Найти эти моменты теоретически можно лишь приблизительно, суммируя действия отдельных элементов, т. е. предполагая независимость действия отдельных элементов друг на друга. Для каждого такого элемента его характеристику приходится брать из испытаний крыла в нормальных условиях (см. Индуктивное сопротивление). На авторотацию крыльев влияют как геометрическая форма крыльев, так и относительная скорость потока и угол атаки. Как показывают расчеты, с увеличением угла атаки увеличивается и угловая скорость

вращения, при чем наиболее интенсивное вращение получается на углах атаки выше критического. С увеличением скорости потока также увеличивается угловая скорость вращения. С другой стороны, при увеличении относительного удлинения крыла уменьшается угловая скорость вращения.

Вследствие взаимного влияния различных частей самолета друг на друга, точного решения задачи о штопоре до сих пор получить не удалось. Необходимы как нек-рые специальные аэродинамич. исследования над моделями в аэродинамич. трубе, так и, гл. обр., исследование штопора над самолетами в натуру. До сих пор удалось установить, что на штопор имеет довольно значительное влияние полол-сение ц. т. самолета относительно хорды крыла. Практически в этой фигуре главнейшую роль играет возможность для данного самолета выйти из штопора. В практике было много случаев, когда самолеты не выходили из штопора и полет кончался катастрофой. Оказывается, что, чем больше вперед распололадн ц. т., тем лучше выходит самолет из штопора; наоборот-при заднем расположении ц. т. самолет выходит из штопора вяло или даже может совсем из него не выйти.

Эксперименты, произведенные в полете, дают наибольшие значения перегрузок от 2 до 4. Английские наблюдения над самолетом FE 2В дали следующие характеристики индивидуального штопора:

Наклон траектории............ = 80°

Угол крена................= 78°

Угол атаки................а = 35°

Радиус витка...............г = 2,Ам

Лит.: ВетчинкинВ. П., Каменеве. И. и Ченцов Н. Г., Динамика полетов, М., 1926; ГоряииовЛ. иКузьминГ., Нормы прочности самолетов при статическ. испытаниях, М., 1926; П ы ш н о в В. С, Самовращение и штопор самолетов, Техника воздушн. флота , М., 1927, 2; его же. Свойства вращающихся крыльев, там же, 1928, 3: У X о в Б. С, Расчет йредвзлётного разбега гидросамолета, там ше, 1928, 5; Balrstow L., Applied Aerodynamics, L., 1920; Devi llers R., La dynamique de Iavion, P., 1920; Blenk H., Startformeln f. Landflugzeuge. Jahrb. d. Deutschen Versuchsanstalt f. Luftfalu-t , Mch.-В., 1927; L a n d e m a n n, G 1 a u-e r t a. Harris, The Experimental a. Mathematical Investigation of Spinning, Technical Reports of the Aeronautics Advisory Committee*, London, 1921, 411; G 1 a u e г t. Investigation of the Spin of an Aeroplane, ibid., 1923, 618; Gates and Bryant, The Spinning of Aeroplanes, ibidem, 1927, 1001; Bryant a. Gates, The Spinning of Aeroplanes, The Journal of the Royal Aeronautical Society . London, 1927, 199. B. Александров.

ДИНАМИКА ПОЛЕТА см. Динамика аэроплана.

ДИНАМИКА ПОРШНЕВЫХ ДВИГАТЕЛЕЙ занимается изучением динамических усилий, возникающих в этих двигателях вследствие периодическ. изменения скоростей движения поршня и шатуна (силы инерции), а также вследствие периодичности действия вообще всех сил двигателя (вибрационные явления). Сюда же относятся и вопросы уравновешивания инерционных усилий и выравнивания вращательных моментов поршневых двигателей (см. Уравновешивание поршневых двигателей). Поршневые двигатели старых конструкций строились для малого количества оборотов и с малыми скоростями движения поршня. На влияние сил инерции движущихся частей двигателя обращалось поэтому мало внима-

Фиг. 1.

НИЯ. Лишь постепенно, с увеличением скоростей поршневых двигателей, сначала в паровых, затем в др. двигателях, конструкторы были вынуждены учитывать влияние этих сил инерции. Радингер впервые в 1867 году частично обосновал теоретически Д. п. д.

Сила инерции поршневых двигателей рассматривается как состоящая из: а) силы инерции поршня и б) силы инерции шатуна.

Силы инерции поршня (фиг. 1). Обозначим через М массу поршня и всех частей, движущихся вместе с ним со скоростью с; через v-окружную скорость пальца кривошипа, R-длину кривошипа, L- длину шатуна, а-угол кривошипа, --угол шатуна. Путь, пройденный поршнем от начального положения:

S = -R (1 - cos а) ± I/ (1 - CCS /3). Здесь знак (+) - для движения кривошипа от начального положения Ад и знак (-)-для движения его от начального положения Bq. Из ур-ия движения поршня определим его скорость

ds sin (а + Р) dt cos;?

= - v (sin а ± sin 2а) .

Ускорение поршня определится:

rcOS (a + /

COSa COSS

COS j3 ~ L

Силы инерции поршня будут, т. о., Pi=--Mip. Приближенное выражение для этих сил инерции имеет вид:

Pi S Ml (ccs cos 2а) .

Существует ряд способов графическ. построения кривых инерционных усилий поршня, наприм. способ Тепле. Очень удобен способ построения этих кривых (фиг. 2) по величинам 11 ординат, равноотстоящих друг

J? 1 2? 1 R

от друга (см. табл. 1)для=-, у-= и у=

Табл. I.- Величины cos ± -jj- cos 2а.

Фиг. 2.

Силы инерции шатуна (фиг. 3). Движение шатуна молшо рассматривать как состоящее из двух движений: поступательного в направлении движения поршня, подчиняющегося законам движения последнего,

и колебательного около своего среднего положения, совпадающего со средней линией

Фиг. 3.

двигателя. Силы инерции при поступат. движении щатуна определятся так же, как и силы инерции порщня, и выразятся так:

rcos (a + /S)

Р=М,--

COS a COS/З.

(cos a ± cos 2a) ;

R ------L

здесь Мг-масса шатуна. Колебате-ньные движения шатуна вызывают инерционные усилия двух родов: 1) силы инерции Q качания и 2) центробежные силы С, возникающие при вращении шатуна вокруг мгновенного центра А. Силы Q определяются путем нахождения скорости качания шатуна Ь- и ускорения этого качания. Для сил инерции

качания шатуна, приложенных в его ц. т., получим, таким обр., следующее вырансение:

Центробежные силы С шатуна определятся из выражения:

и -хИа д jt- cos (3 здесь I-расстояние центра тяжести шатуна от его малой головки.

Равнодействующие инерционных усилийкривошипного механизма. Разложив каждую из полученных нами сил инерции Pi, Р., и С на две составляющие, вдоль средней линии АО и нер-пендикулярно к ней, и суммируя эти составляющие, получим: 1) сумму всех инерционных усилий системы, действующих вдоль средней линии двигателя: P = Pi + P2+<3 sin (М, + М,)

-С cosjS: cos а ±

д cos 2а ;

2) сумму всех инерционных усилий системы, действующих по направлению, перпендикулярному к АО:

cos /5 -f С sin Д = Ма sin а , Если из полученной силы Р вычтем силу.

Табл. 2.-Ф ормулы для определения равнодействующих инерционных

усилий.

-1 (COSa±- . C0S2a)

Т = fei sin а + fea sin 2а + кз sin За + й4 sin 4а

..=-.[м,.м.(.--2.£)]

~ й Й7 L Ч ---L- 2L Щ

2 T = 4&J sin 2a + 4?i sin 4a

lj = 0; 1E = 0 2 T = 6ft, sin 3a

S JC0S45 = /32 M,+ M-~y~.j.

COS 2a

2£ = 0 S r = 8ft4:sin4a