разложить в ряд, оставив только первый член, и тогда получим:

2у8Су(Фо-мС)

(12)

Пренебрегая вторым членом выражения, стоящего в скобках, получим следующую приближенную ф-лу:

= 2у8Су{ф7-

Эта ф-ла во многих случаях практики дает достаточно удовлетворительные результаты.

При расчете разбега гидросамолетов роль трения играет гидродинамич. сопротивление лодки или поплавка, но т. к. кривая водяного сопротивления гидросамолетов в функции скорости не выражается аналитически, а дается обычно в виде эм-пирическ. кривой, то интегрирование пред-взлетного пробега гидросамолета приходится делать графически. На фиг. 9 изображены кривые водян. сопротивления W, воздушного сопротивления Q и тяги винта Ф, при чем ординаты, выражающие воздушное сопротивление, отложены от кривой тяги вниз; ординаты заштрихованной площади представляют для соответствующих скоростей силы, сообщающие гидросамолету ускорение. Если v-скорость гидросамолета в какой-нибудь момент пред-взлетного пробега, то элемент пути ds=vdt, а весь пробег выразится интегралом

-Скорость гидросамшета-Фиг. 9.

S = f V dt .

(14)

Если обозначим через j ускорение гидросамолета во время разбега, т. е. ) = , то время разбега найдется отсюда как

Т=/ jdv. (15)

Необходимые графические построения для нахождения интегралов (14) и (15) даны на

фиг. 10. Сначала строим кривую j в функции от V (I); затем обычным образом строим интегральную кривую f = /(У) = J j dv.

Значение ординаты этой кривой, соответствующее взлётной скорости Ve3A., и будет представлять время разбега гидросамолета. Кривую t=f(v) можно также рассматривать, как кривую v=(p{t), приняв за независимое переменное координату i. Площадь, ограниченная этой кривой, абсциссой, соответствующей t = te3A, и ОСЬЮ ординат (заштрихованная

на фиг.), представляет собою s = / v dt. Опре-

-Схорость гидросамолета-Фиг. 10.

делив эту площадь, мы получим, следовательно, длину S йредвзлётного пробега. Путем последовательного интегрирования мож-

но построить также кривую s=vdt..

Все вышеописанные ф-лы были выведены в предположении, что аэроплан взлетает при безветрии; нетруд-

но вывести форму- Jt-----------.1$?.

лы для соответствующих элементов, предполагая, что ветер дует со скоростью w, так как скорость ветра является переносной скоростью. Аналогично разбегу аэроплана, можно получить и уравнение движения его при

пробеге после посадки. В данном случае, полагая в уравнении (10)Фо=0 и а=0, получим уравнение вида:

-Ql-iG,-lCy)ylv. (16)

Обычно при посадке самолет, подходя к земле, понемногу теряет свою горизонтальную скорость и садится или на скорости больше посадочной, соответствующей углу атаки наибольшей подъемной силы, или равной ей; однако, бывают случаи, когда летчик слишком рано выравнял самолет (т. е. перевел траекторию его полета у земли из наклонной в горизонтальную) или самолет, ударившись колесами об землю, отскочил от нее, теряя горизонтальную скорость. В обоих случаях может произойти след. явление: самолет, потеряв свою горизонт, скорость до посадочной, продоллсает ее терять, при чем, вследствие уменьшения подъемн. силы, он начнет приобретать вертикальную скорость и с силой ударится о землю. Это явление- потеря скорости за границей посадочной и снижение на углах выше критического - называется парашютированием аэроплана. Для составления дифференциальных ур-ий парашютирования можно ввести следующие условия: 1) самолет при парашютировании остается параллельным самому себе; 2) коэфф. сопротивления аэроплана остается постоянным. Уравнения двилсения примут вид:

=-mg sin + Z,

= mgf cos#-t-Z.

Т.к. эти ур-ия не интегрируются в простых ф-иях, то выберем другую систему координат I, Г], С- Пусть ось От] будет направлена по линии равнодействующей воздушных сил, а ось 0 ей перпендикулярна (фиг. 11); тогда получаются следующие дифференциальные уравнения:

= - flf sin г j

Разделив второе ур-ие на первое, получим: = - ctg г -f -г -Ь 2]. (18)

Введем новые переменные т и f I = Ai = - v>u F sin г cos i т

, I -г , (19)

= = увт г cos г С

В начальный момент парашютирования, т.е. когда самолет летит еще горизонтально на посадочной скорости, будем иметь

la=VoCosi, ?]o=i;osini;

подставляя эти значения в уравнение (19), получим:

То = -/ctgi ; Со = 1/tgl. На основании уравнений (19) уравнение (18) приводится к виду:

~ + C + T2 = ctgi. (20)

Это ур-ие есть ур-ие типа Риккати; проинтегрировать его можно одним из способов приближенного интегрирования. Так как при посадке самолета почти всегда бывает небольшое парашютирование, то теория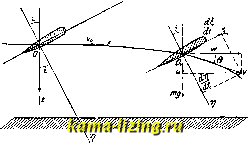

Фиг. и.

парашютирования чрезвычайно ванша для расчетов амортизаторов шасси. Парашютирование самолета можно рассматривать как фиктивное падение тела той же массы в пустоте, при чем вертикальная скорость выразится: и = Vgz , где z-высота падения в пустоте; при этом часть живой силы самолета поглощается ударом шасси и растяжением амортизатора. Часть веса самолета приходится на долю крыльев, обозначим эту долю (1 - i)G, при чем примерно имеет

Фиг. 12.

\р р Фиг. 13.

значение от 0,2 до 0,3 (фиг. 12). Т.о., движение самолета после касания земли сводится к тому, что самолет весом G падает с нек-рой высоты И на землю. Обозначив через h перемещение ц. т. самолета при посадке за счет деформации амортизаторов (шины, амортизационный шнур, прогиб оси ИТ. п.), получим следующее дифференциальное ур-ие движения ц. Т. (фиг. 13):

+ 2P = $G,

(21)

где Р-сила упругости каждой стороны шас-

си, зависящая от h, при чем эту зависимость можно принять линейной, ч.е.Р = Eh (Е можно принять равным 170 кг/см). Подставляя это выражение в уравнение (21), получим:

(22)

Здесь

У т

Общий интеграл ур-ия (22) будет;

fe = .4sin(af-)-fg. По начальным условиям в момент t=0, имеем = О , . Отсюда

а А cos Д = Мо; -4 sin = -. Решая эти уравнения, получим:

рв- г

4£

V Е iE

Таким образом, движение ц. т. аэроплана приводится к гармоническому колебательному движению с периодом

=? = 2л/§. (23)

Максимальная величина хода ц. т. будет:

Отношение максимальной получившейся нагрузки к общему весу, т. е. так называемая перегрузка шасси п, выразится:

max 2Е ,

(25)

Наиболее сложными движениями аэроплана являются криволинейные движения как установившиеся, так и неустановившиеся. К таким полетам относятся т. н. фигурные полеты (см.). К установившимся криволинейным полетам можно отнести вираж и спираль; к неустановившимся движениям относятся мертвая петля и штопор, хотя последний в некоторых случаях можно рассматривать и как установившийся полет. Во всех неустановившихся полетах, а также и при криволинейных полетах подъемная сила аэроплана не равна соответствующей составляющей веса; в этом случае отношение подъемной силы к весу будет называться перегрузкой самолета. Как мы выше видели, при прямолинейном полете подъемная сила всегда равна составляющей веса, и поэтому перегрузки быть никогда не молсет. Перегрузка может получиться или при быстрой перемене угла атаки, так что скорость не успеет еще измениться, или когда имеется постоянная инерционная сила (напр., центробежная). Перегрузка тем больше, чем быстрее происходит перемена положения самолета и чем больше разница в начальном и конечном угле атаки. Т. о., наибольшая перегрузка получается при выходе из пикирования, и чем резче выход, тем больше перегрузка. Положим, что самолет пикирует со скоростью v и летчик, быстро действуя рулями, переводит самолет сразу на прямолинейный полет на критическом угле атаки; тогда подъемн. сила сразу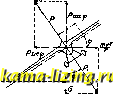

Фиг. 14.

ОТ О достигает величины С oSv, где С наибольшее значение С ; для горизонтального полета на том же угле атаки подъемная сила будет CygSvl, следовательно, перегрузка в данном случае будет: . Перегрузки играют чрезвычайно важную роль в расчете самолета на прочность.

Интегрирование дифференциальных ур-ий криволинейных полетов аэроплана представляет большие трудности и обычно не м. б. доведено до конца; поэтому теоретически приходится решать задачи или прибли- женно или, чаще всего, в числах для данного примера, рассматривая движение от одного положения к другому. Значения перегрузок, необходимых для составления норм прочности, чаще приходится искать экспериментальным путем, т. к. в этом случае учитываются все случайные причины, вызвавшие ту или иную перегрузку. Запись перегрузок на самолете производится так называемым перегрузочным прибором (см.).

Вирал. При вираже на аэроплан действуют следующие силы: 1) подъемная сила крыльев, 2) вес самолета, 3) центробелгная сила, 4) лобовое сопротивление самолета, 5) тяга винта. Вираж называется нормальным в том случае, когда равнодействующая центробежной силы и веса самолета прямо противоположна подъемной силе крыльев; в противном случае получается нек-рое скольжение на крыло. Т. о., виражем называется установившийся полет по круговой горизонтальной траектории; если траектория наклонна, то вираж переходит в спираль. Па фиг. 14 дано расположение сил в плоскости, перпендикулярной продольной оси самолета. Подъемная сила, т. е. сила, перпендикулярная направлению движения и плоскости, проходящей через поперечную и продольную ось самолета, будет выражаться: PCyQSvK (26)

Согласно фиг. 14, будем иметь следующие выражения:

Р cos <f= О; Psin9 = -Перегрузка при вираже выразится:

п = = -- . (27)

G cos <р

Т. О., перегрузка зависит от угла крена: чем

больше крен, тем больше перегрузка.

Из фиг. 14 можно найти и радиус виража.

Действительно, имеем:

Фиг. 15.

(28)

Если обозначим через скорость прямоли-

нейного горизонтального полета под тем же углом атаки, какой имеется в рассматриваемом виралсе, то для горизонтального прямолинейного полета будем иметь:

G=CyQSvl. Принимая во внимание ф-лу (26), получим:

(29)

Подставляя в формулу (28) = - и скорость из формулы (29), получим значение для радиуса виража:

(30)

join gtg<p

Спираль. Движение аэроплана по спирали есть такое движение, при к-ром ц. т. его описывает спиральную линию. Спираль называется правильной, как и в случае виража, когда она производится без скольжения накрыло. Если г - радиус образующего цилиндра, радиус кривизны спирали будет выражаться следующим образом:

(31)

cos &

в случае планирующего спуска по спирали, т. е. без силы тяги, из фиг. 15 получим следующие соотношения {Q-лобовое сопротивление самолета):

G sin = Q G cos = Р cos 9?

;=Psmcp

Деля первое уравнение на второе, найдем угол снижения:

(32)

Р cos (р

- , или tg & =

cos (р

(33)

Перегрузка самолета на спирали найдется из второго уравнения (32): р cos 9 G COSV Если обозначим, как и выше, через скорость прямолинейного горизонтального полета под тем лее углом атаки, как и в дви-лсении по спирали, то будем иметь:

G = CyQSvl. При спуске по спирали подъемная сила выразится:

Р= Оп CyQSv откуда

V \/п ,

Подставляя выражение Р в третье из уравнений (32), получим выражение для радиуса образующего цилиндра ОМ:

G cosi gCygS sin Ф

(34)

или, принимая во внимание ур-ие (33),

G 1 cos° <р

~д CyQS sin <р (cos= <р + /л) Снижение за один оборот по спирали будет равно:

h=2nrtg&, или, вставляя сюда значение г из уравне-