Фнг. 2.

ным координатам наклон аэроплана определится углами а, j8 и у, т. н. углами встречи, сноса и крена (фиг. 2). Если же относить аэроплан к земным осям , то, в зависимости от того, в какой последовательности вращать аэроплан около его осей, получится и соответствующее положение его в пространстве. Будем обозначать через V угол вращения аэроплана около оси Z, через &-угол вращения аэроплана около нового положения оси Y и через у-угол вращения около последнего положения оси X; эти углы называются соответственно углами рысканья, тангалеа и крена (фиг. 3).

Пусть V есть скорость аэроплана по траектории; обозначим через Vrc, Vy, проекции этой скорости на связанные оси координат. Эти компоненты скорости выразятся след. ур-иями: г;а,= г; cos а cos/?, Vy = - vsin, Vg = V sin a cos Д; CKopocTbv будет через них выражаться так:

Обозначим через р, q, г угловые скорости вращения аэроплана соответственно около связанных осей X, Y, Z, через X,Y, Z- проекции внещних сил на них, а через L, М, N-моменты относительно тех же осей, действующие на летящий аэроплан; тогда 6 следующих дифференциальных уравнений и выразят собой движение аэроплана:

Фиг. 3.

m{f + v,r-v,p) = Y m[- + Vyp-v,q) = Z

-ph, + rh, = M -qh,+ ph,N

hi = pA -qF- rE h.,qB~rD-pF \ (1)

h. = rC -pE-qD J a 4, B, C,D,EvL F-моменты инерции и центробежные моменты инерции аэроплана. Центробежные моменты D vlF вследствие симметрии аэроплана относительно плоскости XZ равны нулю, и выражения (1) будут иметь вид: \=рА-гЕ; h.>=qB; \тС-рЕ. В выражения X,Y,Z входит также и сила

тяжести. На фиг. 3 указаны расположения углов д к q) при соответствующих поворотах аэроплана. Т. о., углы между связанными и земными осями выразятся уравнениями:

cos XOZ. = - sin , cos YGZ, = cos 1* sin 9?, cos ZGZi = cos 1? cos 93.

Тогда общие уравнения движения аэроплана будут иметь вид:

{чг + s(7 - v) = - wflf sin -f JX ~ 2) 3 sin 93 -{- Г

m + VyP - v.jij = mg cos cos 95 -h Z A%-E%~qTB-qrC-qpE=L B~ pre + pE + rpA - rE = M ft-E.-pqA + qrE+pqB =N

Здесь X, Y, Z выражают собой только аэродинамические силы, которые действуют на летящий аэроплан.

Интегрирование данных выще дифференциальных ур-ий в общем случае представляет непреодолимые трудности, но и в частных случаях нахождение аналитич. выражения движения не всегда представляется возможным вследствие неимения аналитич. выражения действующих на аэроплан сил. Поэтому обычно возможно применять лищь метод последовательного приближения и решения в числах. Однако, во многих интересных случаях даже и это невозможно, т. к. не получено еще соответствующее выражение сил экспериментальным путем.

Прямолинейный установившийся полет аэроплана. При горизонтальном прямолинейном движении все угловые скорости, а также углы тангажа и крена и обращаются в нуль; из внешних сил остаются только силы сопротивления, сила тяжести и сила тяги винта (Ф); т. о., ур-ия (2) в нашем случае получат вид:

C,qSv-0 = Q, (3)

CyQSv = тд . (4

Это-основные ур-ия аэродипамическ. расчета аэроплана. Сопротивление аэроплана в зависимости от скорости выражается кривой Пэно, которая имеет для скорости некоторый минимум; эта наименьш. скорость полета аэроплана обычно называется посадочной скоростью, так как обычно на этой скорости или близкой к ней самолет приземляется; угол атаки, соответствующий этой скорости, также называется посадочным (или критическим) углом (vnoc, фиг. 4). На кривой коэфф-та подъемной силы этот угол атаки соответствует максим, значению этого коэфф-та. Вблизи посадочн. угла в сторону увличения углов нарушается

Фиг. 4.

ДИНАМИКА АЭР0Н1АНА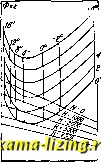

Фш. 5.

прямолинейная зависимость коэфф. подъемной силы от угла атаки, вследствие наступления срыва струй , и кривая, переходя через максимум, начинает снижаться. Посадочная скорость м. б. определена из ф-лы (4):

= -р/-, где Су соответствует максимальному его значению. Если угол атаки больше критического, сопротивление аэроплана возрастает, при чем для лх/ горизонтального полета L требуются ббльшие ско-Г рости. Режим полета, на- чиная с угла, соответствующего наименьшей тяге (Фдшн.) к ббльшим углам атаки, называется вторым режимом, в отличие от первого ре-ж и м а на углах меньших (фиг. 4). На втором режиме полет затруднен, т. к., вследствие малых скоростей , управляемость аэроплана незначительна, и он может сорваться с установившегося движения. Лётным релш-мом является, главным образом, первый режим. О горизонтальных скоростях по высотам и относительно обозначений-см. Аэродинамика, р асчет самолета.

Полет по прямолинейной наклонной траектории. В этом случае, полагая все угловые скорости и угол крена равными нулю, получим основные уравнения следующего вида: x = тд sin или тд sin -& = CgSv- - Ф 1 Z = - тд cos или тд cos & = CyQSv / В последнем случае знак изменился оттого, что подъемная сила аэроплана направлена вверх, т. е. противоположно положительному направлению оси Z. Как и в случае горизонтального полета, можно построить значения величин CqSv в зависимости от скорости по параметру &; тогда получим ряд кривых Пэно для подъема или спуска аэроплана в зависимости от величины & (фиг. 5).

Наклонные прямолинейные траектории полета называются глиссадами. Если будем для данной высоты полета откладывать радиусы-векторы, дающие величину

Фиг. 6.

скорости полета при определенной мощности мотора и ориентированные под соответственными углами тангажа &, то концы этих радиусов-векторов в зависимости от & опишут некоторую кривую, которая называется у к аз ат е л ь н и ц е й глиссад.

, Построение указательницы глиссад делается сле-дуюнщм образом. Строится кривая Лилиенталя всего аэроплана в координатах СудВ=ЕуШ CxeS=Rx, при чем ось подъемных сил направляется гори-

зонтально. Из точек, соответствующих определенным углам атаки, проводятся линии направлений силы тяги, при чем прхшимается во внимание также наклон оси винта к хорде крыла, от которой отсчиты-ваются углы атаки (фиг. 6). Из начала координат О в том же масштабе проводятся дуги окружностей ра-G

диусами соответствующие различным скоростям v

полета. На линиях тяги винта, заключающих между собой одну из окружностей соответствующих скоро-

стеи, откладывается значение - , которое находится

по характеристике винтомоторной группы для соответствующей скорости. Концы этих векторов соединяются кривой-эквидистантной кривой Лилиенталя. Пересечение полученной кривой с соответствующей окружностью даст точку, а после такого построения для всей кривой Лилиенталя получится кривая MN. На продолжении оси ORy проводят в каком-либо масштабе окружности, соответствующие тем скоростям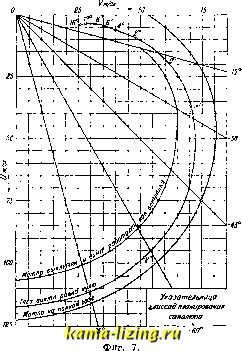

полета, для к-рых строилась кривая MN. Из центра О через какую-либо точку кривой MN проводят прямую, соответствующую определенной скорости, до пересечения с окружностью той же скорости и получают точку, соответствующую вектору скорости по траектории данного самолета. Если произвести такое построение по всей кривой MN, то концы получен, векторов опишут искомую указательницу глиссад.

Из указательницы глиссад видно, что скорости, при к-рых получается максимальный угол подъема самолета, меньше тех, при которых получается наибольшая вертикальная скорость. В тех случаях, когда снижение аэроплана происходит за счет силы тяжести, т. е. без мотора, полет называется планированием. В этом случае Ф=0 и ур-ия движения (2) примут вид:

mgsm&CeSv \

тд cos &=CyQ Sv ( Для планирования можно также очень просто построить указательницу глиссад непосредственно из кривой Лилиенталя. Пренебрегая углом атаки а, примем угол планирования & равным углу между направлением равнодействующей и подъемной силой,

а на поляре-углу между С а и Су (см. Аэродинамика). Проводя из начала координат векторы, соответствуювдие значениям ф-лы

ПОД соответственными углами и соединяя концы векторов кривой, получают кривую указательницы глиссад планирования. При угле планирования 90° планирование переходит в пикирование. На фиг. 7 приведены указательницы глиссад, которые построены для снижающихся прямолинейных траекторий самолета для трех случаев: 1) тяга винта равна 0; 2) мотор работает на полн. газе и 3) мотор выключен, и винт работает как ветрянка. В последнем случае скорости полета оказываются наименьщими, т. к. при работе винта как ветрянки получается большое лобовое сопротивление, почти равное сопротивлению диска одинакового диаметра с винтом и выражающееся следующей формулой:

Схв. = Са, (7)

где Схв.-коэффициент сопротивления винта, отнесенный к площади крыльев, Ср- коэффициент отрицательной тяги винта, F= =0,785 (1)2 - d)-сметаемая винтом площадь, D-диаметр винта, (J-диам. втулки или закрытой коком части винта, S-площадь кры-

льев, а =

C2l ,

средняя относительная ши-

рина лопасти, Z-число лопастей, Ъср.-средняя ширина лопасти, вычисляемая по ф-ле:

> развернутая поверхность лопасти винта Оср. ---

радиус

На основании данных опыта (фиг. 8) можно приблшкенно принять коэфф. отрицательной тяги С постояв-

Фиг. 8.

ным на релшмах винта Я > 5; он изменяется лишь линейно в зависимости от относительного шага винта Ь (см. Воздушный винт). При тяге винта, равной О, и при моторе, работающем на полном газе, разница в скоростях получается сравнительно небольшая, уменьшаясь с увеличением угла наклона траектории.

Надо упомянуть еще об одном прямолинейном установившемся движении-снижении аэроплана со скольжением на крыло. В практике полетов очень часто скольжением на крыло пользуются в том случае, когда на сравнительно небольшой высоте надо быстро потерять высоту, например при посадке на аэродром малого размера. При скольжении на крыло самолет идет обычно с мотором на малом газе (винт почти не тянет), планируя с некоторым углом крена и рысканья. Вследствие того, что при косом направлении полета получается, с одной стороны, увеличение лобового сопротивления за счет эффекта фюзеляжа, а с другой стороны-уменьшение подъемной силы за счет косой обдувки крыла, получаются условия, благоприятные для снижения при посадке (быстрая потеря высоты без большого увеличения скорости).

Неустановившийся и криволинейный полет аэроплана. Движение аэроплана вблизи земли (взлет и посадка). Взлет аэроплана можно рассматривать как движение, состоящее из двух частей: во-первых, прямолинейного, неустановившегося движения по земле и, во-вторых, отрыва в воздух. Нас интересует, главн. образом, первая часть этого движения (до момента отрыва в воздух), которую мы и рассмотрим. Движение самолета по земле до взлета необходимо рассматривать как движение горизонтальное и прямолинейное; уравнения его будут иметь вид:

шд=-Z.

Второе из указанных уравнений существенного значения не имеет, и потому можно ограничиться лишь рассмотрением первого. Внешние силы X, действующ, на аэроплан, будут: сила тяги винта Ф, лобовое сопротивление всего аэроплана Q и сила трения шасси о землю R. Таким образом, первое уравнение имеет вид:

Здесь, как и раньше, принято, что угол тангажа # не велик и проекции сил на связанную ось X заменены самими силами. С целью более простого интегрирования этого ур-ия вводят некоторые упрощающие условия, а именно: 1) во время разбега угол атаки самолета остается постоянным; 2) коэфф. трения шасси ц, к-рым условимся обозначать отношение силы трения шасси к весу самолета, не зависит от скорости движения; 3) силу тяги винта определяют по следующей формуле:

Ф = aov, (9)

где Фо есть тяга винта на месте. Предпо-лагая, что момент взлета соответствует приобретению аэропланом скорости Vg, соответствующей наивыгоднейшему подъему, получаем:

Ж = 0 - - CaQSv-KG -Су oSv), или

t-95=-( + C,-/<C, )r< (10)

где и Су-коэфф-ты лобового сопротивления и подъемной силы всего аэроплана, соответствующие углу атаки, при котором происходит разбег, а у=дд. Интегрируя, получим окончательное выралеение для длины разбега:

G S

где Ct/aсоответствует наивыгоднейшему подъему. Полученная ф-ла чрезвьгаайно громоздка для вычисления, и для приближенных расчетов можно ее несколько упростить. Т. к. член под радикалом всегда положителен и невелик, то все выражение можно