тричной нагрузки все явления в Ж. р, будут симметричные, т. е., если, нанр в каком-нибудь сечении происходит растяясение, то и в симметрично расположенном сечении тоже будет растяжение; если какое-нибудь сечение перемещается при деформации но направлению к оси симметрии, то и симметричное сечение перемещается к оси симметрии. При обратно симметричной нагрузке, наоборот, растяясению какого-либо сечения соответствует сжатие в сечениц, ему симметричном, перемещению точки к оси симметрии Ж. р.-перемещение от оси симметрии для симметрично раснолоясенной точки. Поэтому для каждой из частичных нагрузок число неизвестных в системе будет значительно меньше, чем нри произвольной нагрузке. Если при выбранной уже основной системе общее число неизвестных для решения рамы равно т, то нри решении на симметричную нагрузку будет всего р<т неизвестных, а при решении на обратно симметричную нагрузку т-р неизвестных. Благодаря разложению нагрузок решение системы т совместных ур-ий заменяется решением двух

Фиг. 10.

независимых систем ур-ий общим числом т, что значительно проще. Пусть, напр., требуется рассчитать Ж, р, (фиг. 12,а) на два сосредоточенных груза по 3 т. Размеры рамы и моменты инерции стержней приведены на чертеже. Для расчета абсолютные значения жесткостей стержней EI не играют

роли, важно лишь соотношение жест-

костей стержней. Поэтому ясесткости заменены пропорциональными им числами, приведенными на фиг. 12, б. Основную систему удобно выбрать по фиг, 12, б, т, е. разрезать верхний этаж Ж, р. в коньке, ригель нияс-него этаяса закрепить от боковых смещений горизонтальными стержнями, а узлы А ж А закрепить от поворота. Верхняя часть основной системы статически определима, а нижняя состоит из балок, заделанных обоими концами. При произвольной нагрузке следовало бы в разрезе приложить три неизвестные силы (три компонента силы взаимодействия сечений, разделенных разрезом), ригелю рамы следовало бы дать боковое смещение и повернуть узлы А я. А. Всего было бы шесть неизвестных; из них-три силы и три перемещения. Благодаря симметрии нагрузки можно сказать заранее, что вертикальная составляющая силы взаимодействия в коньке и боковое смещение ригеля будут равны нулю, а узлы А и А повернутся навстречу друг другу на одинаковый угол,

Т. о., остаются всего три неизвестных. Выберем их так: добавим мысленно в месте разреза абсолютно ясесткие стерясни, опускающиеся до нижнего ригеля, и представим себе, что связь между разделенными разрезом сечениями осуществляется через нижние концы этих стержней. Связь обоих сечений была бы при этом не менее полной. Теперь можно неизвестные силывзаимо-действия между частями верхнего эта-

Палма нагрузка

\Z5m

Ситиетричиай часть погрузни

жа приложить к кон- 2т\ цам жестких стержней. Назовем горизонтальную составляющую силы Х, а момент-Хр. Третьей ison/i неизвестной будет угол поворота узла А, к-рый обозначим -через zJg (угол поворота узла А по симметрии имеет ту ясе величину). При действии на основную систему сил Х = 1 vl моментов Х=1 получаются эпюры моментов, изображенные на фиг. 12, в и

12, г. При повороте Обратно сишетричиа! часть />агрр и

узлов А Я А на- Фиг.и.

встречу друг другу

на угол 3=1 рама пстучит деформацию, изображенную на фиг. 12,д. Вьгаислим изгибающие моменты, соответствующие этой деформации. Для ригеля (по таблице опор-пых моментов балки, заделанной двумя концами) находим момент на левой опоре: от поворота левого узла

4£/ А- 50 on I ~ 10

от поворота правого узла

2Е/ 2 50 -.р.

от одновременного поворота узлов Ж = + 10 .

Для верха стойки под влиянием его поворота момент равен

4EJ 4-20 .jp, ,

I ~ 8 -

для нижнего конца стойки

2EZ 2-20

- = -8-=-

По этим значениям моментов построена эпюра фиг. 12, д, при чем, как и во всех остальных случаях, ординаты энюры отложены со

* г I

- Ют-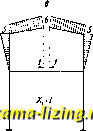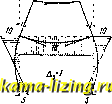

Ч.гтм

Фиг. 12.

стороны растянутого волокна. Построим, наконец, эпюру моментов в основной системе от заданной нагрузки. Благодаря закреплению узлов эпюра занимает только нагруженный стержень. По линиям влияния, для 1=0,2 и =0,8, находим опорный момент:

М = - 3 . 10(0,128 -Ь 0,032) = - 4,8 тж. Эпюра показана на фиг. 12,е.

Теперь можно перейти к вычислению коэффициентов и свободных членов ур-ий. Благодаря симметрии можно ограничиться рассмотрением половины Ж. р. Для вычисления перемещения интегрируем эпюру для = 1; пользуясь таблицей для вычисления

интегралов Мора (схемы 1-1 и 3-3), находим:

(5 + 5

6 + 62) -f

6-5П

= 13,1 .

3 3

Для интегрируем энюры Xi = 1 и Xg = 1; по схемам 1-2 и 1-3 находим:

- = -il[-2(5 + 6) + ] = -2,7.

Из эпюры для Х2=1 по схемам 1-1 и 1-1:

22 = (5 +5,1) = 0,67.

Для определения момента Ж33, развивающегося в закреплении узла А, при его повороте на угол 3=1, вырежем этот узел (фиг. 12, ж) и составим для него уравнение моментов:

Жзз = 10 + 10 = 20 . Коэфф-ты и Ж32 находим аналогично, при чем благодаря переносу сил X на концы жестких стержней получается:

Жз! = -(5i3 = О и Ж32 = -23 = 1 -

Подобным же образом определяются и свободные члены (фиг, 12,3):

1р = 0; 2=0 и Жз=--4,8. В результате получим такие канонич. ур-ия: 13,lXi - 2,7X2 = 0; -2,7X1 -I- 0,67X2 -3 = 0; -Х2-20з-4,8 = 0 . Рещение системы канонических уравнений. Каждое из неизвестных, входящих в канонич. ур-ия, молшо представить в виде линейных ф-ий свободных членов этих ур-ий. Если такое выра-леение найдено, вычисление значений неизвестных не представляет никаких затруднений. Поэтому основная задача при реще-нии ур-ий состоит в определении значений коэфф-тов у в ф-лах:

= иХр + -Jijy + + iiiji + + + Wninp - Vn+l,iXn+l,p - ... - VkiXkp - . Уп+т,1п+т,р > = Пк\р + У>2к2р + .. + Vikip + . +

+ Wnknp - %г+1,кХп+1,р- Пкр -

... yoi+m,kn+m,p

Коэфф-ты Vn-, W2ir , Vib %n представляют собою те силы, а коэфф-ты vji+i,j>

Wn+m,t-те перемещения, к-рыенадо приложить к основной системе по направлениям неизвестных сил Xj, Xj,..., Х,.,., Х, и неизвестных перемещений /l+i,j, Л+ для получения линии прогиба, в виде линии влияния неизвестной силы Х. Аналогично этому коэфф-ты Vifc, Угй VJb Упк, У>п+1,к,---, Укк,--- %г+т,к представляют собой значения тех сил; и перемещений, которые надо приложить к основной системе по направлениям неизвестных сил и перемещений, чтобы линия прогиба представляла собою линию влияния перемещения /1.. На основании теорем взаимности между парами коэфф-тов существует равенство v>ik=Wki-Равенство это справедливо, когда обе неизвестные величины с индексами г,к-силы, когда эти неизвестные-перемещения, а также когда одна из неизвестных-сила, другая-перемещение. Для нахождения величин у) рекомендуется следующий путь: переход от основной системы к заданной Ж. р. совершается постепенно путем изучения ря-

да промежуточных систем. Первая промежуточная система получается из основной введением первой неизвестной: если первая неизвестная - сила, то вводится первая связь, если это-перемещение, то выбрасывается соответствующая связь. Подобно этому введением, кроме первой, еще и второй неизвестной полается вторая промежуточная система, затем третья и т. д. Если число неизвестных равно n + m, то последней промеясуточной системой является (п + + т -1)-я; с введением последней неизвестной получается заданная Ж. р. Так, если при расчете Ж. р. (фиг. 13, а) принята основная система но фиг. 13, б, то промежуточных систем будет всего две (фиг. 13, в и 13, г).

Обозначим далее: через -усилие в последней из введенных связей (или перемещение по направлению последней из выброшенных связей) в г-й промежуточной системе, вызываемое силой =1 (или Л Л Л Л перемещением zl;fe=l, если fc-я неизвестная - перемещение); через rjiii - усилие по направлению Xi (или перемещение по направлению А), вызы-i ваемое в (fc-1)-й промежуточной системе силой Х,=1 (или перемещением /1=1); через <5г(г)-перемещение по направлению Х (если г-я не- известная - сила), вызывае-Л Л мое в (г - 1)-й промежуточной

системе силой Х=1; через Xi{i)-усилие по направлению Af (если г-я неизвестная-перемещение), возникающее в Л Г Л (г-1)-й промежуточной сис-Фиг 13 теме при А=1. Ниже для простоты рассматривается случай, когда все неизвестные - силы. Если-часть неизвестных-перемещения, то следует только заменить силы X перемещениями А, а перемещения по направлению сил X заменить усилиями по направлению перемещений А, взятьши со знаком минус, т. е, вместо (5 писать-ж. Дальнейшееизло-я-сение опирается на ностроении линий влияния неизвестных. Для построения линии влияния первой неизвестной в 1-й промежуточной системе следовало бы дать по направлению Х перемещение, равное ( - 1). Если по направлению приложить в основной системе силу, равную единице, получим .тинию прогиба, подобную линии влияния Xi в 1-й промежуточной системе (модель линии влияния), при чем перемещение по па-правлению Xi равно (фиг. 14). Для получения самой линии влияния надо по направлению Xi приложить силу <Pii равную - ~ Ординаты линий влияния (фиг. 15, а) равны:

Ci2 = 9ii<52i; Ci3 = fpiAi; (в общем случае Си=(Рпп , , fi = = ii ni)- Зная влияние всех сил X на усилие в 1-й связи 1-й промежуточной системы, можно перейти ко 2-й промежуточной системе. Сила Х2=1, ириложенная к 1-й промежуточной системе, вызывает в 1-й связи этой системы усилие j?i2 = Сп- Реакцию 1-го стержня можно заменить внешней силой

>?12 и рассматривать совокупность двух сил- силы, равной 1 и действующей по направлению Xj, и силы, равной г]- и действующей по направлению Х-как группу сил или обобщенную силу ¥2=1, действующую на основную систему (фиг, 14). Тогда

2(2) = 1 22 + ?12<521

Чтобы получить линию влияния Xg во 2-й промежуточной системе, надо приложить вместо 2=1 группу Ф, состоящую из сил

Отсюда (фиг, 15, б)

f 23 = 92232+ 91231

и в общем случае еще

?24 = Pziii + 91241,

Под влиянием силы Хз=1, действующей на 2-ю промежуточную систему, в стержне 2-м возникает усилие ??2з = С2з> в стержне 1-м- усилие

Vl3 ~ 1 Cl3 + 23S12

Совокупность сил 1, ?72з и 77i3 рассматривается как групна Y=l, действующая на основную систему. Масштаб модели линии а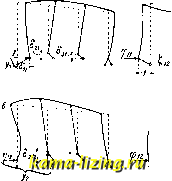

влияния силы Хз в 3-й промежуточной системе, т, е. перемещение <5з(з) определяется по формуле:

з(з) = 33 + *?23<5з2 + Visual-

в общем случае, переходя т. о. от одной промежуточной системы к другой, находят, наконец, силы у> для последней неизвестной Х уже в заданной Ж. р.:

Упп = Vnn = - ;

У in = Ч1п = - ПщРпп-

Линии влияния для сил X в промежуточных системах представляют собой в то же время