Насыщение бетона арматурой а = у.

Приведенная площадь F = Fj, (1 -j-ma). Условное напряясение бетона на сяса-р

тие п= -FT.

<pF

Условное напряжение железа на сжатие тед = тп. Коэфф. (р вводится согласно нормам. Величина а не должна превышать 0,03.

б) Кольцевая и спиральная арматура (бетон в обойме, фиг. 15). Приведенная площадь

F = F,+ 15A + 36/ (7а)

где F,-площадь ядра стойки со спиральной арматурой, -приведенная площадь кольцевой или спиральной арматуры. Наиболь-

f,-общая площадь семений рабочей арттуры

Фиг. 14. Фиг. 15.

Фиг. 16.

шее значение. F:$2Fj, где F-полное поперечное сечение бетона. Величина определится из ф-лы:

где fg-площадь сечения железа кольцевой или спиральной арматуры, s - шаг спирали или расстояние между кольцами, D - диаметр ядра.

VI. Изгиб железобетонных плит и прямоугольных балок при одиночной арматуре (в вытянутой зоне).

На ионеречное сечение действует лишь изгибающий момент М.

I. Общее решение (фиг. 16). Примем следующие обозначения: h-высота балки; Ь- ширина балки; /-площадь поперечного сечения железа; If-момент инерции поперечного сечения яселеза относительно оси, проходящей через его ц. т.; /ij-расстояние ц. т. железа от верхнего края сжатой зоны бетона (полезная высота балки); Ь,,-расстояние нейтральной оси от верхнего края сжатой зоны бетона. В этом случае положение нейтральной оси определяется из одного основного уравнения (5), дающего, так как Р=0,

Sa-mS-mSf=Q,

I Ь(1 - тЦ + (шдЬ/г -f т/)Й2 -

- (\mbh + mfh = 0 . (9)

Второе уравнение (5) в связи с первым (5) дает:

* f + KK-h2)[K-lh]]. (10)

Вычислив /г2 и п, определяют краевые напряжения по ф-лам (6). Для балок и плит

п -{ т

с гибкой арматурой в растягиваемой зоне в формуле (10) надлежит приравнять величину If нулю.

2. Обыкновенная гибкая арматура. Расчет по фазе II (фиг. 17). При mi=0 и lf=0 получим из ур-ий (9) и (10):

l + -t-l

т/

I = m.f(h,- h,)[h,-\}i,) =

(11)

где I-момент инерции приведен, сечения. Краевые напряжения определятся по ф-лам: для бетона

для железа

(12)

Для определения рабочей высоты элемента и сечения арматуры /, нри допускаемом напряжении бетона п и железа rif, мы будем иметь формулы:

(13)

f=CVMb j Коэфф-ты Ci и Са м. б. вычислены заранее для различных величин допускаемых напряжений и определенного m и приведены во всех курсах но железобетону и в справочниках. Для проверки сечений элементов слунсат формулы (11) и (12); для оире-деления же размеров-формулы (13).

3. Двойная арматура. Расчет по фазе II (фиг. 18). Обозначим через f сечение сжатой арматуры, /-сечение растянутой арматуры, tti-расстояние от ц. т. сжатой арматуры до крайнего слсатого волокна (до поверхности) бетона, hi-расстояние от ц. т.

Фиг. г

Фиг. 18.

растянутой арматуры до крайнего сжатого волокна (до поверхности) бетона, h-высоту элемента. Пользуясь основной формулой (5) мы получим при S(i - mSf=0 следующие выражения:

К = [г(/ + П + + V%f + ГУ + 27n(fh, -Ь Га,)Ь] \ \ (14)

1 = 1(1 - 3 hz)bhl + m/(hi - %) (h - а{)

4. Жесткая арматура. Если h-высота прямоугольной балки, b - ее ширина, / - площадь поперечного сечения арматуры,

момент инерции нонеречного сечения железа относительно оси, проходящей через его ц.т.,

1-рабочая высота балки и если не учитывать сопротивления бетона на растялсение (расчет по фазе II), то положение нейтральной оси определится из равенства:

а момент инерции приведенного сечения будет равен

I-m[lf + f(h,-h,){h,-lh,)] . (16)

5. Учет растягивающих напряжений в бетоне. Для прямоугольных балок пользуются ф-лами (9) и (10), принимая в них ml.

VII. Расчет ребристых балок.

I. Одиночная арматура. Сопротивление бетона на растяжение не учитывается (фиг. 19). С принятыми на фиг. 19 обозначениями и

, -ь-

f-общая площадь сечения арматуры

Фиг. 19. Фиг. 20.

если / - площадь поперечного сечения арматуры в растянутой зоне бетона, мы получим следующие формулы для расчета ребристых балок с одиночной арматурой. Положение нейтральной оси определится из выражения:

+ Vldip- b)+mff+d{bb)+ 2тД А } (П) Момент инерции приведенного сечения

-lb[h,-dy(h,-lh,-l)d. (18)

Напряжения: на сжатие в бетоне

на растяжение в железе ( (19)

тМ (/1,-/1,)

При сравнительно большой площади плиты &d но отношению к ребру балки можно для упрощения расчета не учитывать работу бетона (вследствие ее незначительности), заключенного между нижним краем плиты и нейтральной осью (фиг. 20). Тогда получим:

/г<> =

- bd + mfhy 2

(20)

bd + mf

расстояние ц. т. сжатой зоны от нейтральной оси (фиг. 20):

Напряжения: в железе

в бетоне

f (/i,-/i. + y)

т h,- h.

(21)

(22)

Если получается hyd, то нейтральная ось пройдет через плиту ребристой балки, и по-

следняя рассчитывается тогда как прямоугольная балка шириною b и высотою h.

2. Двойная арматура. Сопротивление бетона на растяжение не учитывается (расчет но фазе II) (фиг. 21). С принятыми на фиг. 21 обозначениями, которые означают: /-площадь поперечного f-общая площадь сечв/иясжатоИ арматуры

сечения растянутой арматуры;/!- площадь поперечного сечения сжатой арматуры; h- расстояние от ц. т. растянутой арматуры до крайнего слсатого во-

f-общая площадь сечения растянутой аркатуры Фиг. 21.

локна (до поверхности бетона); -расстояние от ц. т. сжатой арматуры до крайнего сжатого волокна (до поверхности бетона), мы получим следующие выражения для расчета ребристых балок с двойной арматурой. Расстояние нейтральной оси от новерхности балки:

+/ [d( Ь\)+m{f+h)]+b,{b-b)d+2mF,( h J+ aj)} (2 3)

Момент инерции:

I = {bhl {h-lh,)--{h,-dybx

X (1 - 2 -1 d) + m/i ih - tti) (h - a{). (24)

VIII. Скалывающие и главные растягивающие напряжения.

I. Учет скалывающих и главных растягивающих напряжений. Помимо определения нормальных (рассмотренных выше) напряжений, в Ж. к. должны быть также выявлены скалывающие напряжения. Для подверженной изгибу балки скалывающее напряжение в нейтральной оси будет равно

-Ib-b z где Q-поперечная сила в рассматриваемом поперечном сечении; S-статич. момент сжатой или растянутой зоны относительной нейтральной оси; I-момент инерции активного нонеречного сечения; Ь-ширина балки в нейтральной оси; z-плечо пары внутренних сил. Скалывающее напряжение в поперечном сечении бетона с нерабочей растянутой зоной (расчет по фазе II) остается до железной арматуры постоянным и д. б. воспринято сцеплением бетона с арматурой. Величина Z в ф-ле (25) равна (нри принятых в ПН. YI и VII обозначениях): для прямоугольного сечения с одиночной арматурой

для прямоугольного сечения с двойной арматурой и для ребристых балок при учете напряжения сжатия в ребре I

где вместо I д. б. вставлено соответствующее из вышеприведенных выражений. При неучете наиряжений в ребре

В плитах скалывающие напряжения близ опор редко превышают допускаемое для бе-

тона напряжение (4 кг/сж); поэтому здесь обычно нет необходимости в специальной арматуре для их воспринятия. В балках такая арматура необходима, т.к. появляющиеся в них скалывающие напряжения обычно выше допускаемых. Наклонные стержни отгибают под углом 45°, имея в виду, что действующие в нейтральной оси поперечного сечения скалывающие нанряясения по своему значению равны в рассматриваемом месте направленным под углом в 45° главн. растягивающим напряжениям. В балках главные напряжения у оси не должны вообще превосходить величины 14 кг/см, в противном случае необходимо увеличить ширину или высоту балки. Совокупность всех внутрен. косых растягивающих сил у оси в балках должна целиком восприниматься наклонными частями арматуры совместно с хомутами, при чем не учитываются вовсе сопротивления бетона на растяжение и обыкновенно на отогнутые стернши передается около -/з вышеуказанных растягивающих сил. При расчете этой арматуры в менее ответственных соорунсениях участки балок со скалывающими напряяеениями ниже допускаемых не принимаются в расчет. Специальной проверки на скалывание бетона и на сцепление бетона с яселе-зом нри этом не производится. Если в 2 поперечных сечениях, которые находятся на расстоянии Я друг от друга, максимальные скалывающие напряжения равны и tz, то главные растягивающие напряжения им равны, но распределяются только на длину (фиг. 22), Поэтому приходящееся

на длину Я главное растягивающее усилие будет равно

Фиг. 22.

(26)

2. Распределение хомутов и отогнутой арматуры. Распределение противодействующей скалыванию арматуры м. б. сделано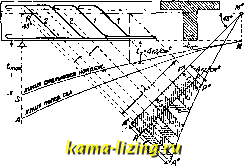

7- одиночный отгиб 2- двойной отгиб

Фиг. 23.

графически следующим построением(фиг.23). Вычерчивают линию поперечных сил МА и отвечающую ей линию скалывающих на-

прянеений MS; ординаты последней

откладьшают затем от линии МА, проходящей через точку М под углом 45° к оси балки; точка М лежит на нейтральной оси балки и отвечает нулевому значению поперечной силы. Если затем от полученной площади МАА напряжений отрезать площадь МРР с наибольшей ординатой = =4 кг/см, то остальная площадь РР АА определит главные растягивающие усилия, не могущие быть воспринятыми одним бетоном. Хомуты воспринимают величину i,. При общем поперечном сечении всех ветве!! хомутов fg и допускаемом их напряясении иа растяжение nf, расстояние менсду хомутами определяется из ур-ия:

(27)

Принимая линию А Р за прямую, получим главное растягивающее усилие:

где - д.тина отрезка 4Р. Необходимое число стержней к для воспринятия этого усилия определится из равенства:

= (28)

где /-поперечное сечение одного отогнутого стерясня; Uf-допускаемое напряжение железа. Чтобы найти располоясение отдельных стержней в балке, площадь растягивающих напряжений A P RR , оставшуюся после вычета напряясения tg, воспринимаемого хомутами, делят на h равновеликих но площади частей (фиг. 23). Ц. т. найденных частей определяют места отгиба стержней. Последние заворачивают в верхней части балки в сторону опор и заканчивают крюками. Хомуты располагают по всей длине балки независимо от данных статического расчета.

3. Расчет напряжений сцепления. Проверки сцепления при наличии отогнутых стерясней и подвесок (хомутов), принимающих на себя все усилия от главных растягивающих напряясений, не требуется. При наличии одних только прямых стержней с хомутами или без них напряжение сцепления определяется но ф-ле:

(29)

где fi-напряжение сцецления, Q-наибольшая перерезывающая сила, U - сумма периметров сечений стеряшей, z-плечо внутренних сил. При наличии отгибов напряжения сцепления определяются выражением

(30)

2 Uz

Некоторые нормы требуют расчета по этой формуле при диаметре стержней арматуры большем 25 мм.

IX. Расчет на сжатие и изгиб.

В том случае, когда осевая внецентренная сила Р не выходит из ядра сечения, напряжения по всему сечению остаются одного знака (сжатие) и краевое сжатие бетона определяется формулой:

Р , , Рее

(31)

Здесь F я I -площадь поперечного сечения