Аг М

где Е и G-модули упругости первого и второго рода, г-радиус колена, 1-полная длина плеча, h-высота плеча (JL оси К. в.), Ь- толщина плеча ( оси К. в.), z-длина цапфы кривоптипа, -полярный момент инерции поперечного сечения цапфы кривощипа,

-s = - аксиальный момент инерции поперечного сечения плеча колена, М -скручивающий момент, действующий на вал, а величина А м. б. получена из уравнения:

щарнирно с К. в. массы порщня и других движущихся прямолинейно-возвратно частей, а равным образом и шатуна, оказывают непрерывно изменяющееся влияние на участвующую в колебаниях массу К. в., причем это влияние изменяется от О в мертвых точках до полного соответствующего значения в половине хода поршня. Так. обр. участвующая в колебаниях масса, связанная с К. в., является переменной по времени. В виду того, что подсчеты при изменяющейся во времени фиктивной массе К. в. очень усложнили бы формулы, по почину Фрама массы частей, двигающиеся прямолинейно-возвратно, вводят в расчет в половинном размере.

где ¥\-площадь поперечного сечения цапфы кривошипа, а v-величина, на к-рую могут перемещаться концы цапф коренного вала в своих подшипниках при деформации К.в. Эта последняя величина вносит известный элемент неопределенности в вычисление значения А. Вообще говоря величина v довольно незначите.ты1а, хотя и колеблется в зависимости от величины nrpi>i в подшипниках и от жесткости основания машины в широких пределах. Предельные значения для нее будут, с одной стороны, t=0, т. е. предполагается совершенное отсутствие игры и абсолютно жесткий фундамент, а с другой -

что равносильно тому условию, что подшипники не представляют н1п%акого препятствия свободной деформации вала под влиянием чистого крутящего момента М. При этом последнем предположении J. обращается так->ке в О и приведенная дтина колена по.лу-чает следующее . значительно более простое выракенпо:

ll + h)br

+ b) , 2,4b , ,4

в этом выражении средний член имеет весг,-ма малую величину и поэтому м. б. исключен, тем более, что этим отчасти компенси-1)уется ошибка, получающаяся вследствие предположения свободрюн подвижности коренных цапф К. в.; т. о. с достаточной для праг:тических целей точностью будем иметь:

Els /з

Массы всех частей вала, неподвижно с ним связанных, для удобства вычислений так-:ке приводятся к фиктивной (приведенной) массе т, сосредоточенной на произвольно выбранном расстоянии R от оси вала; щт-врдение отдельных масс совершают по ф-ле:

где ьнтеграл распространяется по всему объему V приводимой массы fi, п. q представляет собой расстояние диференциала массы от оси К. в., является не чем иным как полярным моментом инерции массы относительно оси К. в.; полагая В,= 1, имеем упрощенное выражение щ!).. Соединенные

Gbh GI

1,186г GFs

К ЭТИМ массам (/л) причисляют массу поршня, поршневого пальца штока, крейцкопфа и определяемую обычным способом (см. Дг<г памика поршневых двигателей) часть массы шатуна; другая часть массы шатуна (ц) считается сосредоточенной в центре цапфы кривошипа и совершающей лигпь вращательное движение; т. о., обозначая через Jj момент инерции массы колена (т.е. двух плеч, противовесов и цапфы кривощипа) относительно оси К. в., получим следующее выра-леение для вычисления приведенной массы одного колена т,. со всеми связанными с ним частями:

Массой центра.льных цп.лнндрич. частей самого вала обычно пренебрегают в виду ее ничтожного влияния на конечный результат.

Для возможности аналитического решения вопроса раз.лагаем кривую периодич. крутящих моментов M = f(o)t) в ряд Фурье:

М = Ао -f .Il sin cot -f- A2 sin 2cot ---f JgSinScof 4-...+ + 2?o + -Bi cos cot 4- B2C0S 2co/ 4- ZJgCOS 3cof 4-...

Разлол-сение диаграммы вращающих моментов для каждого колена с учетом в.лияния инерционных сил производят обыкновенно графическим способом, позволяющим по заданной графически кривой определить коэф-ты членов ряда Фурье. Молшо принять, что действие отдельных гармоник на К. в. складывается; поэтому в дальнейшем будет рассмотрено лишь влияние одного гармонич. колебания порядка h; оба члена ряда Фурье, соответствующих этой гармонике, имеют вид:

Af sin hcot 4- BJ cos hoit. Простейший случай крутильных колебаний, протекающих без затухания, представлен на фиг. 20; лишенный массы отрезок вала д.ли-пой I и постоянного диаметра d заделан одним концом; на противоположном конце закреплена нек-рая масса, к к-рой при.ложен периодически меняющийся момент, разложенный в ряд составляющих гармонических ь;олебапий. Зе.ловия равповесхья в плоскости

А (сумма силы инерции нриведенной массы т, момента внутренних сил упругости скрученного вала и внешних сил должна быть равна 0) выразятся следующим диференци-альньпл ур-ием:

-m -сд?-ь2 (/iSin ha)t+ bji cos о,

h.=l

где gj-угол скручивания вала в плоскости

/у т

а-0.0 = -J--постоянная, учитывающая упругость вала (постоянный член ряда отбрасываем как не участвующий в колебательном движении). Полное решение этого уравнения имеет вид:

9? = со sinj/ + 0 cos / t +

+ 2

где со и /5о-произвольные постоянные интегрирования, выводимые из условий заделки концов вала, а коэфициенты ряда Фурье определяются по формулам:

Аь о Bh

с - тЛсо с - ш h>co

В выражении для <р первые два члена правой части выражают зависимость (р от собствен, колебаний вала, а вся дальнейшая часть- от вынужденных колебаний под влиянием внешних сил. Отсюда получаем угловую скорость частоты собственных колебаний вала:

у 1т

откуда частота

30 / GI

Из выралсения дляа и видно, что они, а следовательно и <р, обращаются в оо, если для одной из гармоник конечной величины

(ajt и В1ф о одновременно) hco=y/~ = a)o,

т. е. если частота собственных колебаний вала совпадает с частотой одной из гармоник (случай резонанса); все эти формулы вы- ведены для идеаль-

Уд в Ф ного случая К. в. , --j- ----3 из материала, ли-

шенного внутреннего трения, при полном отсутствии всех внешн. сопро-

Фиг. 21.

тивлений; при этом условии декремент за-тухания=0, при всех же в действительности существующих веществах он О и, как одно из следствий этого, (р не может ни при каких условиях принимать бесконечно больших значений. Решение задачи в общем виде сводится к нахолсдению в каждый данный момент угла отклонения любой из масс, жестко соединенных с К. в., относительно одной тш масс, принятой за основную. Для этого сначала приводим К. в. со всеми связанными с ним массами к условной форме (фиг. 21) гладкого приведенного вала, имеющего произвольный, постоянный по всей длине момент инерции Jq, к которому на расстоянии приведенных длин 2, 2,3, Afcjt+i, ... , п,пг расположены приведённые массы г !, mj, . , ... , m . В плоскости

вращения каждой из масс действуют изменяющиеся во времени крутящие моменты

Mi,M2,...,Mfe,...,iVf , причем каждый из этих моментов разложен в ряд Фурье:

?г=оо

l-k = s > fki+k,h COS lnoif.i).

h = i

Общий мгновенный угол вынужденных колебаний вала 9? под влиянием этих моментов получаем в виде двойной суммы:

ft=n h=co

9? = 2 s ( t.fc sin hcoi,t -f- ijjcos hmt). fe=i h=i

Частоту собственных колебаний К. в. со многими массами находим, принимая внеш- ние моменты=0 и находя условия равновесия для вала в плоскости калодой массы т. Условия равновесия всех п масс выралсаются системой п диференциальны:з( уравнений:

wi; -bci,2(?i-?2) = o

v + c -i,n(9n-9w-i) = 0

dt

где (pk - угол отклонения массы щ от положения, занимаемого ею при недеформиро-ванном вале, а Ckk+i-упругая постоянная отрезка вала между массами и mjt 4.1, причем

Решая эту систему для угла <Рк отклонения любой массы mjfe, имеем:

п-1 at3(H-i) Л и-2 ajt(n-a) ()tsq

+ 1

аоЧ>

здесь 95;, о и 1-

где а 1, а 2,..., а,..., ai,ao-коэфициенты, получаемые по определенному закону [ij из соответственных значений m и с, а постоянные а и j8 выражаются суммами:

заданные угол отклонения и угловая скорость массы в начальный момент времени. Интегрируя диференциальные уравнения угла q>, получаем общее решение вида:

x=n - i

П = оо* + cto + 2 sin(й) t + е)] ,

где амплитуда колебаний массы и угол сдвига фазы представляют 2(п-1) произвольных постоянных, полученных при интегрировании;

к=п Lmk

к:=п k-i

а сОд. представляет собой модуль ж-го мнимого корня W(j.) характеристического ур-ия 2(п-1)-й степени:

а-м; -! -f w* - + ... + aw+ ... + + aw* + aiv + ао = 0, т.е. W(,y= ±ia) . Следовательно система вала с п массами имеет не одну, а (п-1) различных частот

собственных колебаний, равных ix= <х пер/мин. По уравнению для 9? угол отклонения массы состоит из постоянной части Од, части wt, происходящей от равномерного вращения К. в. с угловой скоростью ojq, и из суммы собственно колебательных углов отклонения. Окончательно получаем в форме, удобной для вычислений, следующую систему уравнений для определения зависимости меледу собой амплитуд колебаний отдельных масс при заданной частоте со возмущающего момента (углы сдвига фаз для всех масс равны между собой, т. е. £j =£ = £3 = = о; == =

h=k~l h=l

<п-1,п

k=n-i

Кроме того в случае резонансной частоты to имеем следующее равенство:

ft-n

2 (ш,С,)=0.

Практически всего удобнее поступать след. образом: сначала находят приблилеенную величину 0)2, сводя число масс к минимуму путем сведения их в группы с массой, равной сумме рядом стоящих масс и расположенной в их общем ц. т.; сведя так. обр. число масс к трем (mi, ma и m с соответственными значениями cig и С2,з), получаем для со биквадратное ур-ие вида:

. co*-co(ci.,i + 4cS3±-?) + \ тша mama /

тхтптз

затем для полученных приближенных значений (О производят точный расчет по следующей схеме:

пенью точности. Величина действительных колебаний вала под действием ряда п моментов, приложенных по длине его, сводится по предыдущему к суммированию влияния отдельных гармонических моментов равного периода. Разлагая действующие моменты в ряды Фурье и отбирая моменты равного периода Q}l = l<ot, равные

и действующие соответственно в плоскостях вращения приведенных масс т, т, т, ...,т , получим для моментов соответственно выражения:

Mii = Aii sin co + Bii cos CO;

Mik = hk sin щ 4- Bjfc cos coi

Mi,n = A,n sin coj -f Bi cos coj. Алшлитуды колебаний отдельных сечений ва.та У1, у2, Ук, Уп под действием всех моментов данных периода и фазы получим путем последовательных вычислений по следующим формулам для каждой фазы А я В\ обозначаем амплитуды, вызываемые фазой А, через С{, Сг,..., С,..., Сп, а фазой В-через С , Са,С ,Сп , тогда получаем:

mi03\C{- Ai,x

Ск = С\-------~

к-к-г

2 ( Л >К + Агд) к~ Ск-1--

СА-ь к

ф-лы для с к отличаются лишь тем, что в них Aijf заменено а С и Ck-i- соответственно через С1 и C-i. Полагая 0 = xviCl=y, получим в конечном счете выражение всех С через хну. Для свободных концов вала сумма всех моментов=0; вследствие этого суммы моментов в последнем свободном отсеке вала по обеим фазам приводятся к виду aiX+bi=0 и 2/4-О, откуда получаем действительные значения для амплитуд и С; общая амплитуда у в данной точке к вала получается из ур-ия:

У, = УСТСГ, угол сдвига фазы колебания в той же точке

№ массы

При со, равном в точности частоте собствен-

НЫХ колебаний со вала, 2 (кк) должна

ft=i

равняться 0; при первом подсчете, вообще говоря, получим величину, отличную от нуля; проделав вычисление для немного разнящейся величины со путем интерполирования, сможем найти значение со с любой сте-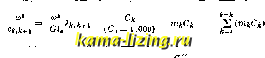

йД-l к-1

£,c - aTctg~r- Обозначим через Ук k+i РЗЗ-

СА;

НОСТЬ меледу двумя соседними углами скручивания в точках к и /с 4- 1; значение ее может быть получено из формулы:

Ук, А+1 = ± VjITI+Tnn+i cos OEi+1 -ej. Тогда максимальное значение касательного напряжения гк+г возникающего на дан-