Фиг. 15.

следний метод менее надежен, чем предыдущий и последующий. Наиболее надежным и очень широко применяемым способом смазки является смазка под давлением (фиг. 14, В). Масло под давлением 1,5-1-2,5 aim поступает в кольцевую канавку коренного подшипника а, отсюда по каналам б-б оно проходит к вкладышу мотылевой шейки в, а отсюда по особой трубочке г часть масла направляется в подшипник пальца поршня. Каналы в цапфах при этом рекомендуется делать большого диаметра и не завинчивать их пробками, а закрывать с обеих сторон особыми крышками, стянутыми болтом; такое устройство значительно повышает надежность смазки сравнительно с узкими каналами и позволяет более легко устранять возможные закупорки каналов. В некоторых конструкциях К. в. каналы для смазки просверливают наклонно (фиг. 7), что значительно облегчает прочистку каналов; при этом необходимо следить за тем, чтобы отверстие не проходило слишком близко от входящих углов в местах перехода цапф в плечи колен вала. В К. в., имеющих длинные плечи колеи, иногда приходится проводить смазку для одной мотылевой шейки от противолежащей; в этом случае простой канал, просверленный в толще плеча, не достигает цели, т. к. в части его, прилежащей к первой шейке, масло должно будет течь против направления центробежной силы и, для того чтобы движение масла вообще было возможным, необходимо, чтобы давление его в канале цанфрл бы.чо бо.тьше, чем давление, вызываемое центробежной силой в канале плеча; т. о. как раз нри больших числах оборотов может наступить такой момент, когда смазка вообще перестанет поступать во вторую шатунную шейку. Д.ЧЯ предупреждения этой возможности каналы обеих ша-тунныхшеек соединяют трубкой а,изогнутой но дуге круга с центром в оси К. в. (фиг. 15).

К. в. находится во время работы иод действием следующих сил: 1) силы давления поршней, 2) веса маховиков и тяги приводных канатов или ремня, 3) силы инерции масс, совершающих прямолинейно-возвратное движение и связанных с К. в. шатуном, 4) силы инерции неуравновешенных порознь вращающихся масс как самого К. в., так и частей, с ним связанных, и 5) реакции под-

шипников. Для расчета цапфы складывают в калхдый данный момент геометрически все силы, действующие на нее, и, беря среднюю силу по времени, определяют размеры цапф из условий допустимой работы трения на единицу поверхности; для определения же условий смазки берут максимальное усилие. Для определения напряжений в К. в. берут последний в нескольких характерных пололсениях, когда можно предполагать возникновение максимальных усилий. Обыкновенно довольствуются двумя случаями: 1) когда одно из колен находится в верхнем мертвом положении, причем в этот момент на него действует полное рабочее давление в цилиндре, и 2) когда одно из колен стоит под углом в 90° к линии мертвых точек. Определение усилий в статически определимом коленчатом вале не встречает затруднений (фиг. 16). В первом положении (фиг. 16, А) на вал действуют силы: -давление поршня, Рг-натяжение приводного ремня, Q- вес маховика и реакции опор А ж В (вертикальные Aq и Bg и горизонтальные-А и Вуу). Схема действия сил представлена на. фиг. 16, Б. Вычерчивая нормальным образом кривые вертикальных и горизон-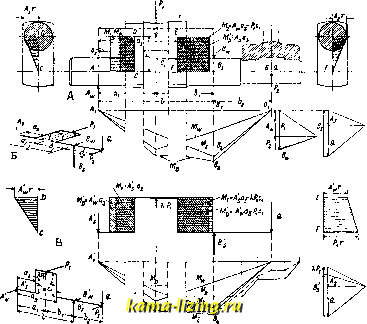

Фиг. 16.

тальных ikf моментов и складывая их геометрически, получаем кривую результирующих моментов Mg, достигающую максимума в точке Bg, где и имеет место максимальное напряжепие в вале

где TFi-момент сопротивления вала. Лево плечо находится под действием сжимающей

силы, равной , изгибающего момента М,

действующего в плоскости колена и равного А-а, крутящего момента М=Аа2, постоянных по длине плеча; кроме того сила Ag вызывает изгибающий момент в плоскости, перпендикулярной плоскости колена, равный Аду; максимального значения этот момент достигает в точке D, где он равен AgV. Соверщенно аналогичным способом определяем моменты, действующие в правом плече. Зная моменты и размеры плеча, выведем в опасных сечениях максимальные нормальные и касательные напрялеения и, складывая их затем, как это было указано в отделе о кривошипах, получим максимальное результирующее напрялеение. Для положения колена под углом 90° к линии мертвых точек (фиг. 16, В) рассуждения остаются теми же, лишь на правое плечо действует в плоскости, перпендикулярной к плоскости плеча, разность изгибающих моментов Pi (г -у) - Ау и на ось и цапфу действует, помимо изгибающих, еще крутящий момент Mjj.

Поверка на прочность статически неопределимых К. в. сводится к предыдущему, как скоро будут найдены реакции онор или опорные моменты. У К. в., лежащего на трех опорах, наиболее удобным способом для определения опорных реакций является способ Мора, причем уменьшение жесткости вала вследствие существования колена учитывается нрибавлением к действующим изгибающим моментам особых фиктивных моментов, которые м. б. найдены нри помощи следующих рассуждений.

1) Колено расположено в плоскости действия силы (фиг. 17). Под действием силы Ро=1, которая действует в точке прилолее-ния реакции среднего подшипника и вызывает реакции опор и В, К. в. примет форму, изображенную на фиг. 17, Б. Реакция опоры Aq вызовет в обоих плечах колена постоянные по длине плеча изгибающие моменты М=Аоа и М =Аоа . Плечо имеет по всей длине постоянный момент инерции cd*

Ijc = И следовательно изогнется но дуге круга радиуса р = с центральным углом Р = ; прогиб точки опоры А вверх под влиянием изгиба плеча 6 = Ва = а. Сравнивая эту формулу с общей формулой стрелы прогиба балок произвольного сечения

отдельные фиктивные усилия, равные

° EJ 1х

видим, что они вполне идентичны: вместо Ij. п X имеются постоянные величины а и

Jfc, а Mdx= RM изобралеает и в этом о

случае площадь диаграммы моментов вдоль плеча колена (фиг. 17, В). Т. о. в диаграмме

;(фиг. 17, Г), которую строят для нахо-

ждения по Мору прогиба балки переменного сечения, можно, положив плечи абсолютно жесткими, ввести на их место как бы

Полученную таким образ, площадь

. .....t------.

при1П1мают по Мору за фиктивную нагрузку балки неизменного сечения и, разделив площадь на ряд элементарных площадок и учтя фиктивные сосредоточенные нагрузки, чертят веревочный м-к, являющийся описанным вокруг упругой линии; сама упругая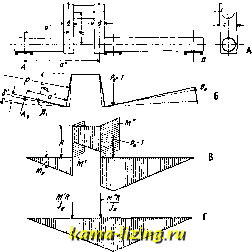

Фиг. 17.

ЛИНИЯ от фиктивной нагрузки представляет собой линию влияния прогиба в точке С действительного К. в. под действием силы, равной 1. Найдя линию влияния, определим реакцию средней опоры С из уравнения:

PnVn

где Р,-действительные нагрузки, iy - соответствующие им ординаты линии влияния и ?У(.-ордината линии влияния силы = 1, приложенной в точке опоры С (см. фиг. 18). 2) Силы действуют перпендикулярно плоскости колена. Линия влияния и величина реакции средней опоры определяются совершенно аналогично предыдущему, с той лишь разницей, что сосредоточенные фиктивные нагрузки, подставляемые вместо предполагаемых абсолютно жесткими плеч колена, равны соответственно

3,6 в и 3,6 Ж Л.

При этом однако остается не принятым во внимание обыкновенно весьма незначительное увеличение деформации К. в., вызываемое изгибом плеча колена и скручиванием шатун, шейки. В общем случае, когда силы действуют под любыми углами к плоскости колена, реакция средней опоры м. б. найдена путем разлонсения всех сил на силы, действующие в плоскости колена и перпендикулярно к ней, и геометрическ. сложения получающихся при раздельном исследовании каждого случая двух взаимно перпендикулярных составляющих реакций опоры.

Для определения опорных реакций К. в., лежащего более чем на трех опорах, описанный способ плохо применим, т. к. в этом случае приходится оперировать с разностя-

ми ординат линий влияния-величинами малыми, причем улсе незначхгтельные ошибки при вьшерчивании могут совершенно исказить весь результат. Удобнее при этом находить моменты, действующие над опорами. Для этого полагаем вал разрезанным на опорах и так. обр. сделанным статически определимым; влияние соседних участков ва.да

Линия прогибаЛиния влияния дляС1 Фиг. 18.

учтем, вводя над опорами изгибающие моменты М, M,, Мд,... (фиг. 19а); при этом ясно, что касате.дьные к обоим отрезкам вала, встречающимся на данной опоре, должны лежать на одной прямой. Для того чтобы учесть влияние колена, о

поступаем, как было описано вьппе, и определяем для каждого от-

Зпюра моментов

Л. Фиг. 19а.

Фиг. 196.

резка по способу Мора углы, получающиеся на концах его: 1) от действительной нагрузки -Ьфиктивные усилия, соответствующие увеличению деформации вследствие существования колена, и 2) от произвольно выбранного момента на опоре, равного М + те лее фиктивные усилия. Согласно правилу знаков, указанному на фиг. 19а, в нервом случае прогиб будет наиравлен вниз (фиг. 196), а во втором случае-вверх (фиг. 19в); для нахолсдепия действительных углов наклона необходимо каждьй! раз приводить вере-

вочный м-к к горизонтальной замыкающей. Тогда окончательно д.дя поля п имеем:

у = у,;-агс tg tgK) + arc tg (? tg й;;) .

<5 = <5; -arc tg (- - tg б; )+ arc tg (f tg у;).

Составив подобные ур-ия для всех и полей и замечая, что 6 = , 6 = 73, ..., 5 i = 7 , а таклсе, что моменты над крайними опорами равны нулю, получим сист. и+1 уравнении для определения 4t + 1 опорных моментов. Если концы вала полагают заделанными, т<> те же it -Ь 1 ур-ий получим, считая у = 6 = 0 и определяя опорные моменты Мд и М над крайними опорами.

3. Крутильные колебания Н.в. Крутильные колебания возникают всегда в более или менее сильной степени нри передаче коленчатым валом периодически изменяющихся моментов. В том случае, когда собственное число колебаний вала как упругой системы равно частоте внешних силовых импульсов или составляет одну из гармоник этой частоты, в результате получающегося резонанса могут возникать частичные деформации и, как следствие их, нанряжения, на много прп-вышающие нормальные, вызываемые действующими внешними силами. Поэтому при всякой новой конструкции коленчатого вала желательно определить собственное число колебаний коленчатого вала, чтобы убедиться, что оно не лелсит в пределах нормальных чисел оборотов данной машины. Особенное внимание крути51ьные колебания привлекли к себе в посчеднее время в связи с созданием быстроходных автомобильных и авиационных моторов. Наиболее удобным способом изучения деформаций К. в. является приведение последнего к фиктивному (приведенному) валу постоянного кругового сечения, обладающего тем свойством, что равные моменты вызывают в нем равные с действительным К. в. углы скручивания. Постоянный, произвольно назначаемый полярный момент инерции поперечного сечения приведенного вала обозначим через Ig, тогда приведен, длина Я любой центральной цилиндрической части К. в. длиной I и диаметром d получится из соотношения:

Зпюра момента

Дтгр.

я = да = г

где Do- диаметр приведенного вала. Фиг. 19в. Приведенная длина

круглого, центрального участка вала длиной I нецилипдрической формы получается из уравнения:

где I-полярный момент инерции соответствующего поперечного сечения рассматриваемого вала.

Приведенная длина Я колена мелсду наружными П.710СК0СТЯМИ, ограничивающими плечи его, молсет быть получена из ур-ия: