Как и выше, в зависимости от м. б. выделено любое число К. д. с периодом Т/2.

Обобщая сделанные вьшоды, можно прийти к заключению, что данная периодич. сила в может в упругом теле вызвать любое

число к. д. с периодами - , где п = 1,2, 3,..., причем уравнения кривых К. д. имеют вид: Р = 4 sin п(а + у) -\-Ап cos п (а +

= Р sin п(а-{-К). (66)

При аналитич. исследовании вопросов, связанных со сложными периодич. К. д., особенно крупное значение имеет разложение данной периодич. функции в ряд Фурье, основывающееся на том, что всякая периодич. ф-ия f{t), не имеющая в интервале 2л бесконечно много максимумов и минимумов и принимающая бесконечно большие значеНИЯ, сохраняя конечной площадь J/(f) ,

м. б. представлена рядом:

со ,

71=1

+ DnCosn{<ot 4-у).

Об аналитич., графич. и механич. способах разложения /(t) см. Фурье теорема и Гармонический анализ.

Нетрудно видеть, что сила, изменяющаяся по закону какой-либо периодич. кривой периода Т, не может вызвать колебаний с периодами 2Т, 4Т, 6Т и т. д. В самом деле: возьмем для простоты синусоидальную периодическую силу в, имеющую период Т = ас (фиг. 13). Очевидно, сила в может вызвать колебание того же периода Т, причем К. д. поглотит импульс, равный разности площадей S - S. Взяв для К. д. период ас> ас и разделив его в точке Ъ пополам, получим, проведя соответствующие ординаты ВЪ и Сс , площади S{ и Sa, причем S- S < Sl- S-Легко заметить, что, чем больше период К. д. приближается к величине ае~2Т, тем меньше будет становиться соответствующая разность площадей, т. е. поглощаемый

Фиг. 13.

периоде, равном ае= = 2Т, этот импульс превращается в цуль, т. е. К. д. периода 2Т возникнуть не может, точно так же, как и периодов 4Т, 6Т и т. д. Наоборот, при периоде, равнол! ЗТ, 5Т и т. д., разность площадей S-Sz, вместе с тем и поглощаемый К. д. импульс, достигают своего максимума. На основании этих соображений периодическ. сила e(f) периода Г может быть разложена в следующий ряд Фурье:

9(<)=2(~-3 -sn- 6 sn----) sin n((ot -f у) + n=l

+ 3 - Usn - ) COS n(o>t -b y) ,

n=l

где An, Asn,--, a; J. ,...cyTb амплитуды тех К. д. порядков п, Зп, Ъп,..., к-рые м. б. вызваны в упругом теле силой 0(i).

В е к т о р н о-к омплексный способ представления К. д. Кроме аналитич. и графическ. способов представления К. д. существует еще векторно-комплекс-н ы й способ представления их, заключающийся в основном в следующем. Допустим, что в плоскости, проходящей через два взаимно перпендикулярных компланарных вектора Fn Fa (фиг. 14а) имеется еще вектор Л, проекции которого по направлениям Fj и Fa суть и ttg. Пусть ось 1, совпадающая с направлением F, есть графич. представление всех действительных чисел, а ось

Фиг. 14а.

фиг. 146.

2, совпадающая с направлением Fg, есть графич. представление всех возмолсных мнимых чисел. Т. о. вектор .4 м. б. представлен комплексным числом а=а1 + аф. Обозначая числен, значение вектора А через г (модуль вектора А), а угол между А и осью 1 через 9, имеем: атсовср, 2=sin у, так что а = г (cos + г sin 9 ), (67),

что на основании формул Эйлера (6) молсет быть представлено также в виде

а = ге. (68)

Нетрудно видеть, что еспи имеется кроме А еще другой вектор В, комплексное выражение к-рого есть Ь= + i&2j то комплексное выражение вектора суммы А+В будет равно алгебраич. сумме комплексных выражений слагаемых векторов, т.е. равно а -Ь Ь = = (а-Ь bj) -Ьг (tta-b Ь. Если Ъ представить в виде Ъ = ee**. то алгебраическ. произведение аЬ представит новый вектор аЪ=где\ модуль к-рого равен rq, а угол, образованный им с осью 1, равен (р+. Если в частности у=0> то вектор а при умножении лишь удлиняется в q раз, сохраняя свое направление, если же е = 2,то вектор поворачивается лишь на уго.ч у, сохраняя свою величину. В более общем случае имеем:

gim?> r (cos т<р + г sin ш??). (69)

Рассмотренный способ изображения векторов удобен при исследовании периодическ. колебаний, разлагаемых в ряд Фурье. Основное колебание = sin (со i-f-j) м. б. представлено след. образ.: отрезок ОР = а, (фиг. 146) вращается с постоянною угловою скоростью со вокруг О, так что в момент t угол между ОР и осью i равен си f-fdj, если в момент f=0 вращающийся отрезок отстоял от оси 1 на угол . Проекция же ОР на ось -2 равна sin (со i+(5i). Так. обр. колебание может рассматриваться как изменение мни-

мой части вектора, представленного комплексным числом ае. Другое, синхронное с первым, колебание

может быть также представлено как изменение мнимой части комплексного числа г(а)( + п) представляющего нек-рый другой вектор. Сумма рассматриваемых двух колебаний

Oj sin (со t + j) 4- 1 sin (to t -f У1) может т. о. рассматриваться как новое результирующее колебание, представленное изменением мнимой части комплексн. числа

1(ш( + у,)

1{ш1 + Ъ)

Если ОР есть вектор, представленный первым комплексным числом, а PJV-вектор, представленный вторым, то ON=PN+OP

есть вектор, представленный ае *так что весь процесс слолеения двух данных колебаний м. б. рассматриваем как измене-HPie проекции вращающегося с постоянною угловою скоростью О) около О треугольника OPN на ось мнимых количеств. Если составляющие колебания синхронны, то множитель е * м. б. опущен, и тогда тр-к OPN неподвижен в пространстве. Чтобы получить мгновенные значения как слагаемых, так и результирующего колебаний, нужно проектировать неподвижный тр-к OPN на прямую, вращающуюся около О с постоянною угловою скоростью -о), т. е. в обратном по отношению к первому направлению. Т. обр. получается т. наз. диаграмма колебаний. Диаграммы колебаний более сложных видов применяются особенно часто в электротехнике (см. Генератор переменного шока. Индукционные машины).

Как легко усмотреть, все дифер. уравнения разобранных выше случаев К. д. представляют собою частные случаи следующего линейного дифер. ур-ия 2-го порядка:

Mx,t) -Ь Ai(x,t) -{-A2ix,t)x +

+Аз(х,1) = 0, (70)

где коэфициенты А, А, А и А-ф-ии от х и t. Во всех рассмотренных выше случаях эти коэф-ты были величинами постоянными. При ААзО получается вид дифер. ур-ия <4), при Аз=0 получается вид дифер. ур-ия (31) и т. д. При более сложных случаях К. д. получаются однако дифер. ур-ия более общего вида (70). Аналитич. методы интегрирования дифер. ур-ий вида (70) довольно сложны и потому для практич. надобностей весьма мало пригодны. Гораздо более быстрые результаты с достаточной для практики степенью точности дают графические методы интегрирования дифер. ур-ий, приводимых к рассматриваемому виду или даже к еще более общему виду:

лишь бы последние бьши разрешимы отно-, т. е. представляемы в виде:

сительно

\dt

X, t).

(71)

Из графич. методов интегрирования дифер. ур-ий рассматриваемых видов укажем в общих чертах на следующий метод. Пусть имеются следующие начальные условия дви-лсения точки: при t=fi, хх и v = Vi, т. е.

cci. По отношению к двум взаимно перпендикулярным осям X к t (фиг. 15) эти начальные условия движения определяют некоторую точку Al и нек-рое направление dj. Из ур-ия (71) имеем:

XI =fix{,Xi, tj) ,

а из известного соотношения

где Q - радиус кривизны кривой х = x{t), имеем радиус кривизны искомой кривой в точке J-i, а именно:

-/(1+ Qi--

Зная Qi и направление dj, найдем соответствующий центр кривизны Oj, т. к. ОА = перпендикулярен к d. Проведя из 0 радиусом Qi соприкасающуюся окружность и взяв на этой же окружности достаточно малую дугу А1А2, получим точку А2, которая приблизительно будет находиться на искомой кривой и которой будут соответствовать новые значения 2 и 2 и новое направление х. Поступая по отношению к точке А2 точно так же, как и по отношению к А, получим новую точку и т. д. т. о. моншо искомую кривую X = x(t) определить с любой степенью точности как состоящую из отдельных малых дуг, принадлежащих различным соприкасающимся окружностям.

К.д. в различных областях тех НИКИ. К. д., обнимающие почти все области техники, м. б. подразделены на К. д. с одной степенью свободы и К. д. со многими степенями Свободы (см. Механика теоретическая). KnepBoit категории относятся напр. колебания фундаментов под влиянием К. д. машин, колебания быстро вращающихся валов, колебания кручения быстро и медленно вращающихся ва.тов, движения автоматич. клапанов в поршневых насосах и т. д. К К. д. с несколькими степенями свободы относятся напр. колебания двойных маятников, центробежных регуляторов, маятниковых тахометров, инерционных регуляторов, турбинных регуляторных систем, рулевых механизмов судов и т. п. Исследования К. д. имеют особенно существенное значение при движении судов, паровозов, аэропланов, при явлениях движения волчков, при исследовании жироскопич. сил и т. д. В теории упругости особенно валеное значение имеет исследование колебаний струн, эластичных пластин (мембран), продольных и поперечных колебаний стержней. В строительном деле исследуются вопросы, связанные с колебаниями мостов, фундаментов, башен, маяков

Фиг. 15.

и т. п. В областях, связанных с исследованием деталей машин, рассматриваются колебания различных пружин и рессор. Большую роль играет исследование К. д. в гидравлике, в особенности при установлении законов движения волн и образования вихрей, движения лсидкости в трубопроводах и в сообшающихся сосудах и в частности в гидравлич. машинах и т. п. Крупное при-1Сладное значение имеет исследование колебаний пара в соплах паровых турбин. Аналогичные проблемы возникают при исследовании законов движения газов и паров в трубопроводах. Фундаментальное значенпе имеют К. д.в акустике, базирующейся целиком на установлении законов К.д,воздушной среды. С этими лее проблемами связаны и вопросы строительной акустики, теории музыки, конструирования музыка.чьных и акустических инструментов и т. и. Громадная область прикладной и теоретич. электротехники , теория электромагнитных колебаний, теории квант и новейших статистич. и волновой механики целиком базируются на исследовании вопросов, связанных с видом К. д., и наконец в таких областях, как физиология, биология и метеорология, исследования К. д. имеют крупное значение.

Методы и приборы для непосредственных измерений механических К. д. могут быть подразделены различным образом в зависимости от точки зрения. Так напр. с точки зрения областей применения их можно подразделить на следующие группы: 1) сейсмометрические в широком смысле слова-измеряющие либо колебания эластичных, но неподвижных в целом систем, либо колебания систем, находящихся в движении (землетрясения, колебания почвы, колебания фундаментов машин, колебания судов, мостов, ферм, К. д. поездов, аэропланов и т. п.);

2) измеряющие переменные механич. воздействия (напряжения в частях мостов, судов, аэропланов, кручение валов и т. п.);

3) индикаторные (индикаторы паровых машин и двигателей внутрен. сгорания, измерения колебательных давлений жидкостей и газов и т. п.); 4) приборы общего машиностроения (техника синхронизирования, равномерность хода ременных и зубчатых передач и т. п.); 5) акустические-связанные с измерением звуковых колебаний; 6) физиологические и биологические-измеряющие колебания в живых организмах. По роду регистрации К. д. их можно подразделить на механически, оптически и электрически регистрирующие. К сейсмометрическим приборам, в широком смысле слова, принадлежат в первую очередь приборы, измеряющие колебания почвы: сейсмографы и клинографы (см. Сейсмология).

Для измерения колебаний судов применяется паллограф О. Шлика, конструкция которого в основе состоит из следующих частей: 1) приспособления, регистрирующего вертикальные колебания, 2) приспособления, регистрирующего горизонтальные колебания, 3) часового механизма, приводящего в движение цилиндр с полоской бумаги и отмечающего на ней промежутки времени, и 4) регистрирующей части. Схема упомянутого паллографа О. Шлика предста-

влена на фиг. 16. Горизонтальные колебания судна вызывают колебания горизонтального маятника М, а вертикальные?-колебания вертикального маятника (см. Маятник). Относительные смещения грузов маятников передаются при помощи системы рычажков пишущим штифтам А п В, наносящим соответствующие кривые на полоску бумаги, приводящейся в движение цилиндром 1С при помощи часового механизма С. Третий штифт D, находящийся под воздействием часового механизма Cj, отмечает на полоске бумаги интервалы времени. Так как маятники наряду с вынулсденными колебаниями имеют еще и собственные периоды колебаний, могущие исказить истинный характер регистрированных колебаний, то особенно важно придать прибору такую конструкцию, при которой достигались бы по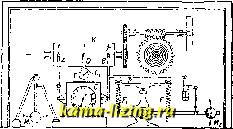

Фиг. 16.

возможности значительные периоды собственных колебаний, и иметь кроме того возможность регулировать эти колебания. У вертикального маятника первая цель достигается след. образом. Маятник, врашающий-ся около оси S, опирается в точке Е на конец вертикальной пружины F, причем точка Е лежит ниже обычного горизонтального положения оси стержня маятника. В зависимости от расстояния точки Е от оси стержня м. б. получен больший или меньший период собственных колебаний. В паллографе точка опоры Е м. б. смещена в желаемом направлении. Вертикальный маятник паллографа снабжен двумя пружинами F и F, соединенными рычагом R с целью уменьшения вертикальных размеров прибора и возможности случайных смешений оси пру-Лгины. Обычная частота колебаний вертикального маятника прибора Шлика равна 20 в минуту; при этом прибор в состоянии правильно регистрировать колебания с частотой до 40 в мин. Горизонтальный маятник состоит из тяжелого металлическ. цилиндра (фиг. 17), подвешенного горизонтальной своей осью ZZ к двум стержням h и h. могущим перемещаться во втулках b и b. С другой стороны, эти стержни могут вращаться на цапфах, укрепленных на стержнях а, а. Втулки Ь, b соединены между собой горизонтальным стержнем, могущим вращаться вокруг оси d. Последняя при помощи конич. зубчаток к, к может приподниматься или опускаться. Период собственных колебаний Т горизонтального маятника зависит от величины И = р + q - r, где р-рас-