д е к р е-

ваемую логарифмическим

ментом затухания и равную

Наблюдая за амплитудами колебания, можно легко определить логарифмическ. декремент затухания, а затем и коэф-ты пи а, определяющие величину торможения среды. Откладывая по оси абсцисс время t, а по оси ординат соответствующие значения х, получаем графич. изобрал-сение (35), представлен-яое на фиг. 10. В технике К. д. с линейным затуханием рассмотренного типа встречается довольно часто. Примером величины, затухающей по приведенному выше закону, может служить напряжение разряжаемого конденсатора, включенного последовательно в цепь вместе с омическим и индуктивным сопротивлениями. Если С - CiMKocTb конденсатора, R - омич. сопротив.11ение, L-коэф. самоиндукции, то напряжение s у клемм конденсатора ©пределяется в ф-ии времени из дрхфер.ур-ия:

dt L dt LC

Т. е. из дифер. ур-ия, имеющего вид (32). Сравнивая (38) и (32), получаем:

фиг. 10.

Г. + Т WV+77: = О

(38)

2п = ;

-LC

Т. к. выше условием для получения К. д. служило наличие неравенства h>n, то условием д.тя получения колебательного разряда с переменным напряжением е служит неравенство;

2L ♦ С

/LC

>

Если же последнее условие не соблюдено, то разряд анериодический. Все вышеприведенные выводы применимы конечно и к рассматриваемому случаю; так, в частности пе-рио.т колебания разряда равен:

Vh-n*

у LC 4.L

Более сложным случаем затухающего К. д. является тот, когда сила сопротивления среды пропорциональна квадрату скорости. Тогда вместо дифер. уравнения (31) имеем:

g + 2тп (~У + Г-тх = 0. (39)

Рассматривая как нек-рую неизвестпую

переменную, имеем, интегрируя (39):

-/ (г-4п . + Се- ). (40)

Есчи начальные условия движения таковы,

что, при f = О, = О, а ж = - о, то

С = -е-* (1+4мао), так что вместо ур-ия (40) имеем:

d.ii dt

h}.[1-4пж-е-* < * >(Ц-4иао)]. (40)

Следующую за -амп.питуду о. получим из (10), приравняв левую часть ур-ия нулю и

заменив ж через а. Таким образом получает-ся трансцендентное уравнение

Vw [l-4 a,-e-* >(l-f4пао)] , (41)

к-рое м. б. решено относительно лишь методом постепенного подбора значений а. Если же разложить правую часть (41) в ряд и отбросить члены, содержащие о или в степени выше третьей, то получается следующая приближенная формула:

или в общем виде:

a, = a, i(l-f а, г). (41)

Из (41) видно, что уменьшение амплитуды составляет тем меньшую долю предшествующей амплитуды, чем меньше величина последней. Полный период колебания равен

[1-4пж-е-* <*П1+4пао)]

Вынужденные К. д. Если на материальную точку помимо вышеприведенных сил действует еще сила 0, линия действия к-рой совпадает с линией действия прежних сил и величина к-рой есть нек-рая периодич. функция времени t, то упомянутые выше результирующие движения точки будут этой силой периодически изменяться, вследствие чего сила в носит название возмущающей силы. Чаще всего величина силы В берется в виде следующей функции от t: q sin tjf. В зависимости от того, какие из прежних сил F, Q, Т VL Ф приложены одновременно к материальной точке помимо 0, могут представиться различные случаи, из которых рассмотрим лишь два следующих.

а) Вынужденное К. д. при наличии одной лишь силы притяжения , пропорциональной расстоянию. Если на точку действует кроме Q лишь одна силаР =-Яж, то дифер. уравнение движения имеет следующий вид:

m 5-ЬЯ2ж = Ksinjjf, (42)

или, если обозначить через I:

-Ь ?с-ж = 1 sin(43)

Для того чтобы проинтегрировать (43), можно поступить след. обр.: взяв производные два раза по t от обеих частей (43), т. е.

% + h%=-WBinnt, (44)

и умножив обе части (43) на tj, сложим полученный результат с равенством (44). Тогда получим:

(45)

dt dt Характеристич. ур-ие для дифер. ур-ия (45), т. е. ур-ие

имеет корни q = ± щ п q = ±ы. т. о. общий интегра.л дифер. ур-ия (43) будет

ж= Се+Ч Се-Ч Се++ Се,

что может быть при помощи приведенных формул Эйлера (6) представлено еще и в следующем виде:

X = Ai sin (Tit + Yi) -Ь Az sin (kt -f y). (46) Это и есть у[:>-ие движения точки в ее результирующем движении. Как видно из (46), результирующее движение состоит из двух составляющих гармонических К. д., а именно: К. д. $i=Asin(r]t+yi), вызьшаемого наличием возмущающей силы в и называемого выну ж д е н н ы м колебаниегл, и собственного К. д. точки 2=2 sin (Л: i + Уз) вызываемого наличием силы F. Период первого колебания Tj, совпадающий с периодом силы в. равен , а период второго ксчебания

. Из четырех постоянных ур-ия (46),

Al, У1, А . лишь последние два определяются начальными условиями движения, первые :ке два определяются из предыдущих данных след. обр.: из (46) имеем:

==-A,yfHin(vt\+yx)-A. kmn(kt+y2): (47) подставив (47) и (46) в (43), получаем:

Al (к - г]) sin (rjt + yj) = г si,n Tjt. Так как пос.теднее ур-ие должно удовлетворяться при всех значениях t и при постоянных J.i и У1,то это требование возможно лишь при У1 = 0 и i(/c2-7?2)= I, т. е. при yiO и

Al = ту*-i. Ур-ия результирующего движения (46) и вынужденного движения принимают при этом следующий вид:

X = .4., sin (kt + Уа) + , . sin r]t, (48)

b=feisin 7t. (49)

Есчи период Т. возмущающей силы в совпадает с периодом Tl собственных колебаний, т. е. если /с=??, то, как видно из (48), х принимает бесконечно больгпое значение. В этом сл\ае говорят, что имеется явление р е-3 он а н с а. Если tj становится больше к, то li имеет знак, противоположный знаку 2, т. е., другими словами, у свободного и вынужденного колебаний имеется сдвиг фаз, равный по.довине полного периода.

б) Вынужденные К. д. при наличии сопротивления среды. Если на материальную точку, кроме сил F и в, действует еще сила сопротивления среды, пропорциональная 1-й степени скорости, т.е. сила (р = -av, то дифер. уравнение движения принимает вид:

т + а у- -\- Х х = К sin i]t,

d-x dt

)in - + kx =1 ninrjt

(50)

(51)

T. k. дифер. ур-ие (51) отличается от (32) тем, что в право!! части (51) вместо О стоит выражение lsinr]t, то, найдя частный интеграл (51) и прибавив его к общему интегралу (32), найдем общий интеграл (51). Для этого, нололсив

X = р sin rjt-j-г COS r]t, (52)

найдем такие значения для р и г, к-рые, будучи подставлены в (52), дали бы ж, удовле-

творяющий (51). Для последней це.ти имеем из (52):

= PV cos Tjt - rt] sin r]t i

dx (

= -pyf sin r]t - rif COS rit I

что гюсле подстановки в (51) дает:

sin rit (-рп-2nrri-\-k-p-l)-\-+ cos nt (-ГТ] -f 2np7] + кГ) = О ,

(53)

откуда

РП + 2пгг}-кр + г = о, rrf - 2прг] - к-г = О,

2ПТ11

4nV (ft - *?) I

(54)

Общий интеграл принимает при этих значениях риг следующий вид:

X = е-* (Ci sin pt + Сз cos pt) -\-

+ (p sin Tjt -f- r cos Tjt) ,

0- = е-* A sin (pt + У2) + Al sin (r]t + y), (55) причем на основании (И) и (И)

А, = VCl-\- CI; Al = Vp -Ь г

(56)

Из (55) видно, что результирующее движение состоит из одного затухающего колебания с убывающею амплитудою e~ *-.i42 и вынужденного колебания с амплитудою Ai. Подставляя в (55) значения р и г из (54) и произведя необходимые преобразования, получаем следующее значение д.чя последней амплитуды:

Отсюда, видно, что, по мере приближения значений щ к значению к, Ai все возрастает и при резонансе, т. е. при ч = достигает своего максимума, равного ~ . Чем меньше при

этом W, т. е. чем меньше сопротивление среды, тем больше амплитуда JL,. При w=0 мы получаем такой резонанс, как в предшествующем случае при отсутствии силы Ф. Примером для рассмотренного случая колебаний может служить изменение силы тока, протекающего в электрич. цепи, в к-рую последовательно включены: конденсатор емкостью С, индуктивн. сопротивление с коэфициен-том самоиндукции L, омич. сопротивление R и источник тока с синусоидальным изменением напряжения е=Е sin соf. Дифер. ур-ие изменения силы тока г имеет при этом следующий вид:

Li + R%C-Esin,

dH , R di , 1 . £ .

т. е. получаем дифер. ур-ие, аналогичное (51), так что все полученные выше выводы будут применимы к закону изменения г, если положить

2ti = -f

- CL

В более общем случае возмущающая сила 0 может быть нек-рой произвольной периодич.

ф-ией времени t, так что дифер. ур-ие (45) принимает вид:

Е(х)=в(1), (57)

где Е{х) представляет собой левую часть ур-ия (42), а 6(f) данную функцию в. Если 0(0 есть сумма периодич. функций времени ®2(0> пСО то, найдя частные интегралы II, Ja, I,t ИЗ дифер. ур-ий Е(х) = e,(ty, Е(х)=в,(1У,...; ад=0 (О. получим общий интеграл уравнения (57) в виде 1 = =Ii+ I2 + + 1 , что и определяет сложное К. д., вызванное одновременным действием эластичной силы F и данной периодхгч. силы в. Если в частности кансдая из составляющих периодическ. сил в имеет вид, аналогичный правой части (42), т. е.

e=.Ksinr]t ... (v= 1,2, ... , n), (58) то соответствующий интеграл 1 имеет вид, аналогичный (46), т. е.

а;- sin (rjj -f у) -f л; (kj + у;), что показывает, что каждая из составляющих сил 0у будет вызывать нек-рое вынужденное колебание А sin (rjt + у).

Исследование К. д. упругих тел (в частности частей машин или тел, соединенных с последними), находящихся под воздействием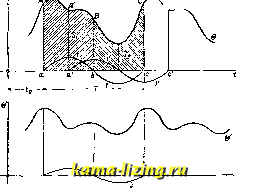

Фиг. 1 1 .

периодич. сил, имеет во многих областях техники громадное значение (вибрации поршневых двигателей, колебания мостов, колебания фундаментов машин и т. п.). Допустим, что кривая АБС (фиг. 11) есть периодич. кривая, выражающая функхщональную зависимость в от t, причем Т= ав есть период полного изменения силы 0. Пусть, далее, сила 0 действует на упругое тело (или на часть нек-рого упругого тела), имеющее период собственных колебаний, равный также Т. Площадь S, ограниченная частью АБС кривой, ординатами Аа и Сс и осью абсцисс, представляет собою полный импульс силы 0 в промежутке от t~to до t-tQ+T, т.е.

J e(t)dt.

Рассматриваемое упругое тело моиеет под действием силы 0 совершать гармоническое К. д., представленное синусоидой 1, с периодом = Т, поглотить при этом импульс силы, равный разности площадей Sj-Sg, где Sj-площадь, ограниченная частью АВщт-вой, ординатой Аа, ординатой ВЬ, проходя-

щей через середину Ъ отрезка ос, и осью абсцисс, а §2-аналогичная площадь ВСсЬ. Уравнение кривой 1 молеет быть представлено в виде:

A = Ai (sin r]t+ У1) = Al sin (a -f Vi) =

= sin[f (f-fo)] . (59)

Сдвинув ординаты Аа я Bb на. четверть периода, найдем аналогичным способом новую кривую I возможного гармонического К. д. тела с тем же периодом Т, но имеющего ур-ие

А = А{ sin (jilt -Ь J+ г1) = 1 cos (а -f У1)

= .lisinP(<-b-fo)]. (60)

Результирующее лее К. д. будет иметь ур-ие Р = sin Са -Ь уО + Al cos (а + у), (61) что может быть приведено к виду:

P = P,sin(a-byO. (62)

Так. обр. из данной периодич. кривой 0 м. б. выделено в зависимости от Уг или какое угодно число гармонич. кривых (гармоник) периода Т, выражающих возмоленые Ko.7ie6a-ния упругого тела. При нек-ром определенном значении у амплитуды Ai и А достигнут максимальных размеров, что будет иметь место при равенстве ординат, проходящих через io и fo + /2 . Максимальная величина Pi определяется равенством:

Р\ +А .

тах тах * max

Вычитая далее из ординат данной кривой 0 соответствующие ординаты гармонич. кривой i, получим новую периодич. кривую в, выражающую остаточную периодическ. силу, к-рая может в свою очередь вызвать К. д. 2, опреде.тяемое так лее, как и выше.

Данная периодич. сила 0 может вызвать также гармонич. колебания с периодом Т/2. Для выделения соответствующей кривой 2 (фиг. 12) разделим асТ на четыре равные части и, проведя через точки деления ординаты, разделим площадь S на четыре части Si, S2, S3, S. К. д. 2 поглощает импульс

Фиг. 12.

силы, равный разности площадей (Sj 4- tS3) - - (S2 + Si),a уравнение кривой2 будет ил[еть вид, аналогичгплй (59), а именно:

А = А. sin 2 (а -Ь У2)= sin

(t-to)

(63)

Передвинув затем ординаты на четв*рть пе-рргода, получим еще одно возможное К. д. с периодом Т/2, уравнение которого будет: А =ACOs2(a + y2) . (64)

Ур-ие лее результирующей кривой с периодом Т/2 будет:

Р = 2 in 2(а -Ь у,) -f А2 cos 2(а -h У2) =

= P2sin2 (о-ЬуО . (65)