ют с направлением оси х: одна из них есть сила притяжения к некоторому центру О, прямо пропорциональная расстоянию от материальной точки до точки О, а другая-сила, постоянная по величине и направлению. Пусть начало отсчета оси х взято в центре притяжения О. Обозначая первую силу через F, а вторую через Q, имеем попрежнему Р = -}?х, а Q = Const, так что дифер. ур-ие движения точки будет:

d3c dt*

fc2 =

-f fc-cc и 6

(22) (23)

Нетрудно видеть, что дифер. ур-ие (23) м. б. приведено к типу (4) и что следовательно и в рассматриваемом случае точка будет совершать гармоническое К. д. В самом деле из (23) имеем:

или, если X -

Z, то

(24)

т. е. получаем дифер. ур- иетипаХ4). Так как центр колебания, определяемого (24), находится в точке z=0, то расстояние х от центра колебания С до начала отсчета О, совпадающего с центром притяжения, определяется из равенства:

Т.о. видно, что центр притяжения О уже не совпадает с центром колебания С, как это имело место в рассмотренном выше случае.

Точка С отстоит от О на расстоянии = j,

в сторону действия постоянной силы Q. Так

как далее есть частный интеграл дифер.

ур-ия (23), то, принимая во внимание, что (7) есть общий интеграл дифер. ур-ия (4), получим общий интеграл дифер. уравнения (23) в следующем виде:

ж = Ci sin fci +Са cos fcf-b,- (25) Отсюда имеем:

v= Cik cos kt - Ck sin kt. (26) Если в начальный момент точка находилась в О, имея при этом нулевую скорость, т. е. если ж = 0 и v=0, при f=0, то Ci = 0 и

С2=-так что вместо (25) и (26) имеем:

-g coskt + l; V -sin kt.

X--: cos kt + ~; (25)

(26)

В частности, силою Q может служить вес тела Р=тд, а силою F-сила натяжения вертикальной пружины. Тогда вместо ур-ий (23), (25) и (26) получаем соответственно уравнения:

ж = -, cosfcf + , г-= sin/cf.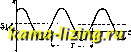

Фиг. 6.

Откладывая значения ж по оси ординат, а значения t по оси абсцисс, получаем кривую, изображенную на фиг. 6.

Примеромдля рассмотренного вида К. д. может служить горизонтальная балка, опирающаяся на две опоры в двух точках An В я нагруженная посредине грузом Р, причем весом самой балки пренебрегаем. Если I-д.лина балки между А п В, I-момент инерции поперечного сечения балки, Е- модуль упругости, то статич. прогиб а балки под действием силы Р будет:

4S ЕI

и.ли, если обозначить -через А,

а = , или Р = аА2.

Под действием силы Р балка в положении равновесия будет иметь изогнутый вид. Для того чтобы прогиб ба.лки стал ж, нужно, чтобы на середину балки действовала сила

Р, но при этом отношение р

няться отношению

должно рав-т. е. Р = Аж. Если

балку вывести из состояния покоя, то она начнет колебаться, причем в положении, определяемом прогибом ж, на середину балки будут действовать две силы: сила веса груза Р=тд и сила упругой деформации самой балки, стремящаяся привести ее в горизонт, положение и пропорциона.льная величине ж, т. е, сила Р = -А-ж. Ур-ие движения середины балки принимает в таком случае вид, аналогичный ур-ию (22), а именно:

ш=~х + тд, или +.кх==д.

Середина ба.лки будет т. о. совершать гармоническое К. д. около нек-рого центра колебания, отстоящего к н и з у от прямой АВ на расстоянии

д дт Р . I fe Я ~ 48Е7 *

Все прочие общие выводы применимы и к этому частному случаю.

К. д. под действием силы при-тялсения, пропорциональной расстоянию, при наличии силы трения. Если точка массы т, находящаяся под действием силы притяжения, пропорциональной расстоянию ж от точки до некоторого центра притяжения О, перемещается по шероховатой горизонтальн. плоскости, то при движении действуют на точку следующ. силы: сила притяжения F =-Аж, сила веса Р=тд, сила трения T=fmg (где /-коэф. трения движения) и сила реакции п.лоскости R.T.K. сила Т, оставаясь постоянной по величине, меняет свое направление в зависимости от направления движения точки (этим сила Т отличается от силы Q предыдущего случая, сохраняющей постоянными как величину, так и направление), то ур-ие движения точки будет менять свой вид в зависимости от того, движется ли точка справа налево и.ли наоборот. В первом случае, т.е. при t;<0, сила Т направлена в положи-

тельную сторону оси (фиг. 7), так что дифер. ур-ие принимает вид:

(27)

при движении же слева направо, т. е. при v>0, ур-ие движения будет:

-lx-lmg. (27)

Фиг. 7.

Рассматривая 1-й случай, имеем из (27):

+ r-xfg, (28)

где fc* = . Так как полученное ур-ие (28)

вполне совпадает по виду с дифер. ур-ием (23), то отсюда следует, что, при рассматриваемом движении точки справо налево, точка совершает гармоническое К. д. около некоторогоцентра колебанияО!, отстоящего от центра притяжения О на расстоянии жо1= , в сторону действующ, силы трения Т, играющей т. о. роль силы Q. Общий интеграл дифер. ур-ия (28) будет, аналогично (25),

.г - Ci sin fcf-l-Ca cos fci-b-g- (29)

Если ж = Жх и у = 0, при t = О, т. е. если время начать отсчитывать с того момента, когда точка, отведенная в сторону на расстояние предоставлена сама себе, то ур-ие движения (29) принимает следующий частный вид:

x=(xi-g)cosfef-bg- (30)

Отсюда имеем также выралеение для скорости:

u = -(a;i-g)fcsinfcf. (30)

Скорость V вновь превратится в О, при условии, что sin fcf = О, т. е. при Ы = л или * = В этот момент х будет иметь след. значение:

т. о. по абсолютному своему значению второй полуразмах х меньше первого полуразмаха 1 на 2 0 . При последующем движении

точки слева направо уравнение движения будет вида (27), а вместо ур-ий(ЗО) и (30) будем иметь соответственно:

х = [-х,+ ЩсоШ-% ;

v = {x2 fcsin Ы . Так как скорость v вновь превратится в О спустя опять промежуток времени , то третий полуразмах Жд будет:

Ж2-2-0, и т. д.

Из рассмотрения дифер. ур-ия (27) видно, что в своем обратном движении точка опять будет совершать гармоническое К. д., но уже около центра колебания 0, отстоящего слева от О на расстоянии . В своем дальней-

т. Э. W.. X.

шем движении справа налево точка опять совершает гармоническое К. д. около центра Оз, совпадающего с прежним центром 0, и т. д. Полуразмахи же ж, Жг, Жд,... по своей абсолютной величине образуют убывающую арифметическую прогрессию, так что

Ж2 = Жг - 2 т

ж,-2

ж -4-

Фиг. 8.

a -.,-i-2g = x,-2(n-l)g.

Полуразмахи не стремятся стать бесконечно малыми. Движение точки прекратится, если какой-нибудь полуразмах х становится по

абсолютному своему значению меньше 2 , т. к. в этом случае не может иметь места равенство ж,.+1=ж-2 (ж + 1 и 0 суть положительные величины). Как видно из предыдущего, промежуток времени между положениями точки Жх и Жд равен ; таков же и

промежуток времени между положениями точки Жз и Жб и т. д. Т. о. период полного колебания будет и в рассматриваемом случае равен Т , несмотря на убывание величины

размахов. Такое движение называется изохронным. Откладывая значение ж по оси Of)динат, а значения t по оси абсцисс, получаем кривую, представлен- fg ную на фиг. 8 и со- ЧЛ

стоящую из отделЬ- г

НЫХ частей синусоид АОВ, ВОС, COJD,.., причем для этих частей центрами симметрии служат 0, 0, О, О ... располагающиеся попеременно на прямых KLi и К.Ь2, отстоящих с обеих сторон от

оси t каждая на расстоянии .

В качестве примера рассматриваемого вида /твижения могут служить движения грузов в регуляторе Гар-тунга(фиг. 9)во время вращательного движения последнего около -ч своей оси. Пусть конец пружины, прижимающий груз J. к грузу А, в спокойном состоянии отстоит от оси вращения KL на расстоянии Жц. Если привести стержень MN в равномерное вращательное движение около вертикальной оси KL, то груз А сожмет пружину. В положении, когда конец пружины отстоит от оси KL на расстоянии ж, на груз А действуют следующие силы: центробежная сила m = шжа)2 (где ю-угловая скорость вращения), сила трения о стержень,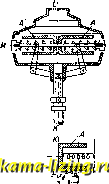

Фиг. 9.

равная mgf (где /-коэф. трения), и сила напряжения пружины Х{х - Хо), где -фактор пропорциональности между напряжением пружины и ее сжатием ж -Жд. Т. к. все эти силы действуют по направлению оси стержня MN, к-рую берем за ось X, то уравнение движения груза принимает следующий вид:

W = тхо)- - (х - Жо) ± mgf ,

или, обозначив ж-ж через

W = - (А2 - шт) + т(а)2жо ±gt).

-(Jc-a,2(coXo±gf).

Таким образом получим дифер. ур-ие, аналогичное (28), вследствие чего грузы регулятора будут совершать движение по вышеприведенному закону.

К.д. под действием силы притяжения, пропорциональной расстоянию, при наличии сопротивления, зависящего от скорости. Во многих физическ. явлениях движение тела встречает со стороны среды, в к-рой двилсение происходит, сопротивление, являющееся нек-рой ф-ией скорости. Самым простым случаем является при этом тот, когда сопротивление среды прямо пропорционально первой степени скорости. Если в частности иметь в виду сопротив.чение движению со стороны воздуха, то при не слишком болыпих скоростях с ббльшим или меньшим приближением такая прямая пропорциональность в действительности существует. Еще точнее такая прямая пропорциональная зависимость имеет место при движении магнита около медной массы, встречающего при этом сопротивление движению со стороны индуцированных токов. Если на материальную точку действует кроме силы напряжения F = - Дж еще и сила сопротивления среды, пропорциональная скорости v, т. е. сила b = - av, где а-фактор пропорциональности между Ф и V, а знак минус указывает, что направление силы Ф противоположно направлению v, то диференциаль-ное ур-ие движения будет: d*x

m = -Дж -at;,

(31)

или, обозначая через 2п ,

g-f 2п-ЬЛ;ж = 0. (32)

Если сопротивление среды невелико по сравнению с силою Е,то к> п, что обычно и имеет место. Положив ж = е, найдем те значения /3, которые удовлетворяют ур-ию (32),

а именно:

р = -п± Vn-k\ (33)

или, в предпололсении, что к> п,

fi = - n±i Vk-n: = - п±рг,

где p-Vk - n. Отсюда имеем общий интеграл дифер. ур-ия (32):

ж= С\вЧ С,е= е [С/ -f С.е] , (34)

что при помощи форму.д Эйлера (6) принимает вид:

a; = e~ [(7sinp<-f-(7 cosp<], (35)

а скорость

V = е~ [Ср cos pt - Ср sin pt ] -- пе

(35)

[С sin + С COS pi]. Если, при i=0, ж=0 и v = Vq то

так что ур-ия (35) и (35)принимают следующий частный вид:

= 5e- sinpf, (36)

[р cos pt - п sin pt] . (36)

Из (36) следует непосредственно, что движение точки будет колебательное с периодом колебания

2я 2я

Таким образом К. д. и в этом случае изохронно; однако, в то время как при наличии силы трения период колебания точно такой же, как и при соответствующем свободно.м гармоиич. движении, в рассматриваемом случае период Т меньше периода свободного колебания. Ур-ие (36) отличается от ур-ия гармонического К. д. лишь фактором В начале двилсения, когда время t еще мало отличается от О, этот множитель мало от.тичается от 1, всяедствие чего К. д. будет мало отличаться от гармонического; это будет длитьс51 тем дольше, чем сопротивление среды, т. е. коэф-т п, меньше. Но по мере увеличения времени t последующие амплитуды будут все более резко уменьшаться, стремясь к пулю при t= оо. Очевидно ур-ие (36)-дает значения последовательных амплитуд при значениях sin pt\ -1, т. е. при значениях pt = ,;

Зя . 5я . , (2г-1)п

~2 2 2 Зя . . (2г-1)я

2р * 2р

тельные амплитуды будут следовательно:

-, или при значениях t

Соответствующие последова-

(гт1)пя

(37)

Т.о. последовательные амплитуды составляют геометрическ. убывающую прогрессию со

знаменателем, равным е . Такое К. д. называется затухающим. Так как

то, взяв натуральный логарифм от обеих частей последнего равенства, получаем:

1п a-f-i - In = - - ,

1пХ-1па,.+1-,

(37)

так что натуральные логарифмы двух произвольных последовательных амплитуд отличаются на одну и ту же величину, пазы-