что и служит к непосредственному сведению его к нулю. Сложный электронно-ионный процесс, происходящий в вольтовой дуге, сильно искажает форму колебаний, поддер-лшваемых ею в контуре. В зависимости от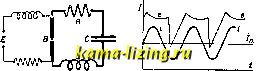

Фиг. 13.

Фиг. 14.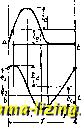

Фиг. 15.

условий, В которые поставлена вольтова дуга,-напр. от возмолшости быстрого охлаледения ее электродов (их температура определяет электронную сторону процесса) и быстрой деионизации воздушного промежутка,-колебания получаются трех родов (Симон, Баркгаузен). Колебания 1-го рода <фиг. 14) представляют собою синусоидальн. ток, налагающийся на постоянный 1,. при сильно искаженных колебаниях напряжения на конденсаторе. Колебания 2-го рода (фиг. 15), являющиеся наиболее валеными Д.ЛЯ техники, происходят при ма.том за время Та ток отсутствует; Tj м. б. получено в пределах меледу л ]/ LC и 2 л УЬС Колебания 3-го рода (фиг. 16) подобны тем сериям затухающих колебаний, к-рые возбуждаются исьерой (фиг. 9); кривая изменения напряжения на конденсаторе показывает нарастание его во время отсутствия тока в контуре до той величины, при которой залеигается вольтова дуга; благодаря последней снова начинаются колебания. Фиг. 14 -16 показывают своим сложным видом, в какой малой степени явления, производимые дуговым генератором , отвечают потребности практики в чистых ctraycon-дальных колебаниях с постоянной амплиту-,дой. И тем не менее техника достигала удовлетворительного разрешения своих задач, хотя при этом и требовалось большое искусство управления дуговою схемой.

в) К. э. при помощи электронной лампы. За последние 10 лет вошел во всеобщее употреб- и ление новый метод по- лучения незатухающих колебаний-при помощи электронной .тампы. Лампа вклю- 4 чается параллельно колебательному контуру (см. выше фиг. 17); здесь пользуются отрицательным сопротивлением в ответв.тении. Разрядный процесс в электронной лампе, особенно если она эвакуирована до технического предела, значительно проще, чем в вольтовой дуге; поэтому аналитическое выражение действия ламповой схемы п,тем ряда прибли-леений (Валлаури, Баркгаузен, Бонч-Бру-евич, Шоттки, Ван-дер-Поль) получает все

Фиг. 16.

Фиг. 17.

большую точность. Ламповая схема получила дальнейшее усовершенствование, и в то же время усложнение, в виде стабилизатора. Дело в том, что режим, с которым работает лампа, легко может несколько измениться, что ведет к изменению даваемого схемой периода-изменению небольшому, но уяее недопустимому при современных методах радиопередачи. Во пзбелеание этого явления в схему вводится вещество (пьезоэлектрическое И.Ш1 магнитострикционное), в к-ром под действием электрич. колебаний возбуледаются механич. колебания, оказывающиеся необычайно устойчивыми; влияя обратно на электрические процессы, они стабилизуют электрическ. колебания. Рассмотрение таких схем приводит к ди-ференциа.тьным уравнениям высших порядков, с которыми

давно улее приходилось иметь дело в теории колебаний связанных систем (М. Вин, Мауц. Татаринов), обогатившейся за последне; время понятием о затягивании (см. Ламповые генераторы).

Следует упомянуть в заключение о совсем новом понятии параметрических колебаний, практич. применение которых ещ только предвидится, и о так назыв. нетом-соновских колебаниях. При этих последних самоиндукция контура играет второстепенную роль и м. б. очень малой; они происходят, если R>2j/, что делает невозмол:-

ifbiMH ко.тебапия томсоновские; их период определяется величинами С и R. Из многочисленных схем, применяемых радистами и физиологами для получения нетомсо-новских колебаний, упомянем ту, которая основана на свойстве неоновой (тлеющей) лампы 1 АДА I пропускать ток .тишь при дости-{ УУ неенпи известного напрялсеыия Eq на ее электродах. Источник постояпного напряжения Е > Е через сощ-ротивление jR заряжает емкость С (фиг. 18); по достилео-нии емкостью напряжения Eq неоновая лампа разряжает конденсатор, который затем снова заряжается. Промелеуток времени меледу двумя зарядами регулируется величинами С и R.

Лит.: Э,лектрическис колебания и волны, сб. под ред. в. Лебединского, вып. 2, СПБ, 19J1; П е т р о г,-с к и й А., Радиосети (литогр.). Л., 1924; его и; е, Научные основания беспроволочной телеграфии, ч. 1, СПБ, 1913; Ивановский В., Теоретич. исследование колебании в связанных спстемах. П., 1917; фрейма ы И., Курс радиотехники, 2 изд., М.-Л., 1928; Л у цепко Н. Н.. Основы теории радиотехники. Л., 1927; ТиТбП с 1918; Nesper Е., Handb. d. drahtl. Telegraphic п. Telephonie, В., 1921; о 1 I e n d о г 1 Г F., Grundlagen d. Hochfrcquenztech-nlk, Berlin, 1926; Zen neck .1. u. Rukop h.. Lehrbuch d. drahtl. Telegraphie, 5 Auflage, Stg., 1925; Pierce G., Electromagnetic Oscillations a. Electric Waves, N. Y., 1920. B. Лебединский.

КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ, движение, при котором материальная точка (или тело) периодически проходит иод воздействием приложенных сил через одно и то же пололеение устойчивого равновесия. В

Фиг. 18.

Фиг, 1.

зависимости от характера приложенных сил К. д. бывают различны. Основными видами К. д. являются следующие.

К. д. материальной точки, находящейся под действием силы притяжения, пропорциональной расстоянию. Пусть нек-рая материаль-

д ная точка А массы

Г 1 т (фиг. 1) находит-

--i >j-ся под действием

силы F, притягивающей ее к некоторому центру притяжения О, причем пусть абсолютная величина F силы будет пропорциональна расстоянию точки от О. Пусть, далее, положение А по отношению к нек-рой системе отсчета, имеющей начало в точке О, определяется радиусом-вектором г. Нетрудно видеть, что векторы F \\ г, находясь на одной прямой X, направлены в противоположные стороны, и т. к. кроме того JF и т прямо пропорциональны, то

2=-AV, (1)

где - существенно положительный фактор пропорциональности между величинами F и г. Так как по основной формуле динамики (см. Механика теоретическая)

то получается следующее ур-ие шее двилсение точки А:

опреде.чяю-(3)

или,обозначая для простоты абсолютную величину вектора г через ж, а - через If,

Проинтегрировав последнее диференциаль-ное ур-ие, найдем функциональную зависимость переменной величины ж от времени t, а взяв далее производную ж по t, найдем и функциональную зависимость скорости v от времени t, т. к. точка А двилсется прямолинейно по оси ж. Обе найденные т.о. функциональные зависимости вполне определяют характер движения материальной точки. Общий интеграл дифер. ур-ия (4) имеет следующий вид (см. Диференциальные уравне)1ия):

X = Се* + С е-\ (5)

где е-основание натуральных логарифмов. Пользуясь ф-лами Эйлера:

g+ Ш gQg дд g-)

можно общему интегралу (5) придать еще и следующий вид:

ж= CiSinfcf-Ь CaCosfcf, (7)

где Ci и Са-нек-рые постоянные, опреде-.тяющиеся из начальных условий движения. Взяв производную ж по t, получаем из (7):

vv = = C-kcoskt-Cksinkt. (8)

Если в начальный момент точка А находилась в О, имея скорость Уо,т. е. если ж=0 и v = Vq при f=0, то постоянные интеграции и Сг принимают след. частные значения:

так что равенства (7) и (8) принимают следующий частный вид:

ж = \ sin М, (9)

vVgCokt. (10)

При других начальных условиях движения постоянные С, и имеют конечно другие значения. Пусть а и у-две постоянные, связанные с постоянными и Сг следующими соотношениями:

Ci = acosy, C2 = asinj, (11)

так что

ayCl + a и tgy=

(11)

Вставляя значения (11) в (7), получаем третий вид общего интеграла дифер. ур-ия (4), а именно:

x=asin(kt -\-у). (12)

Из рассмотрения равенства (12) можно неносредственно сде.аать следующие выводы. 1) Так как правая часть (12) периодическая ф-ия от t, то и величина ж периодическая ф-ия от t, т. е. точка А будет периодическрг находиться на одном и том же расстоянии от центра О, другими словами, точка А будет совершать К. д. около О. 2) Абсолютная максимальная величина ж равна а = ОВ =

= ]/С + С; это максимальное расстояние Л от О называется амплитудой колебания. 3) Если время t увеличивается на промежуток времени Т = , то и расстояние ж принимает прежнее свое значение. В самом деле, если в момент f = + точка А находится от О на расстоянии х, то Xi = а sin (liti -Ь у) = а sin jfc (t -f -f у j = = a sin (fcf -f- y) = Ж. Промежуток времени Т = , по истечении

которого точка вновь находится в прежнем своем положении, называется полным периодом колебания. 4) Так как dx

ак cos (kt + y),

(13)

то величина v достигает максимума, когда ж=0, т. е. точка А будет иметь наибольшую скорость при прохождении через центр О. 5) Т. к. ускорение j равно в данном случае

j==-aksm{kt + y), (14)

то? = 0приж = 0 и jJmax при V=0, т. е. при прохождении точки А через пололсение О ускорение ее равно нулю, а в точках возврата ускорение достигает максимального своего значения. К. д., обладающее вышеуказанными свойствами, называется гармоническим. Кинематически гармоническое К. д. может быть представлено стед. обр. Пусть нек-рая точка движется равномерно с постоянною угловою скоростью к по окружности радиуса а, имеющей центр в точке О. Пусть начало отсчета угловых перемещений будет ОМ (фиг. 2) и пусть при f =0 точка находилась в положении Pq. определяемом углом РоОМ=у. По истечении времени t угловое перемещение точки равно kt, а угловое расстояние от начала отсчета углов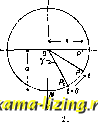

Фиг.

равно Ы-\-у. Проектируя точку в ее положении Р на прямую ОХ, нерпендикулярнун1 ОМ, получим проекцию Р, отстоящую от О на расстоянии ОР =х=а sin (kt+y). Т, о. видно, что проекция на диаметр окружности точки, совершающей равномерное круговое движение, совершает гармоническое К. д. Механич. -X схема, соответствующая вышеуказанному кинематич. представлению гармонического К. д., приведена на фиг. 3, где: АВ-кривошип, О-неподвижная ось кривошипа, С-ползун, D-E?-шток поршня, KL-поршень. Нетрудно усмотреть на основании сказанного, что если кривошип будет равномерно вращаться около оси О, то поршень будет совершать гармоническое К. д. Исходя из этих кинематич. соображений, величину kl -\- у правой части (12) называют фазовым углом, или фазой, К. д. в момент t, а у-н а ч а л ь н о й фазе й.

Если по оси абсцисс ортогональной системы осей координат откладывать значения t, а по оси- ординат - соответствующие значения X из (12), то в результате получается синусоидальная кривая, представляющая графически изменение X в зависимости от t (фиг. 4). В общем случае кривая пересекает ось ординат в Р, так что ОР=Х(,а sin у,т.к. .это соответствует моменту =0. Кривая пересекает ось абсцисс последовательно в точках Al, А2, A3, отстоящих друг от друга

на расстоянии, равном -. Два К, д., имеющих один и тот же период колебания, называются синхронными. Если имеются два несинхронных К. д.

x = asm(kt -{-у) и ж= аsin (fcf-f у), так что кфк, то разность фазовых углов (kt-j-y) - (kt-i-y) называется сдвигом фаз в момент t. Так как при синхронных колебаниях к=к,то сдвиг фаз двух синхронных колебаний равен в любой момент начальному сдвигу фаз у- у. Величина 1 ft

V = У = -, показывающая, сколько полных колебаний совершает точка в единицу времени, называется частотой колебания,

К типу дифер. ур-ия (4) приводятся во многих случаях дифер. ур-ия движения, как например ур-ие движения математич. маятника, т. е. материальной точки, вынужденной перемещаться но дуге окружности. Связью, вынуждающей точку совершать движение по окружности, может стужить либо нерастяжимая нить длиною I, закрепленная в некоторой точке О, либо шаровая поверхность

Фиг. 3.

радиуса I с центром в точке О (фиг. 5). Параметром, определяющим пололеение точки в положении С, пусть будет угол ВОС=а, где ВО-вертика.тьная прямая, проходйщая через точку О. Пусть в момент t=0 точка находилась в положении А, определяемом углом Oq, имея скорость v=0. В положении С на точку, при отсутствии сил трения, действуют сила веса JP= тд и сила реакции связи JR, так что Щ) = Р + В, (15) илиР + B - mJ=0, где j-вектор полного ускорения точки в рассматриваемом положении. Т. к. проекция j на направление касательной /с равна по абсолютному значению

Фиг. 5.

d(l(o) d(o i d*a dt ~dt~dt*

a при движении сверху вниз

, d*a

то, проектируя (15) на это же направ.те-ние, получаем:

ml -Ь тд sin а = О ,

rg + gsina.

(16)

(17)

При малых колебаниях можно, вследстврю малости угла а заменить sin а через а. Тогда вместо (f7) имеем приближенную формулу:

4-fa = 0, (18)

аналогичную дифер. ур-ию (4), где вместо коэф-та fc2 имеем . Общий интеграл имеет поэтому вид, аналогичный (7):

а = Сг sin (j/ f t) + C2 cos (j/ f t) , (19) a угловая скорость со равняется

-C./fsin(? t).

(20)

При данных нача.яьных устовиях движения Ci = 0, С2 = а(, так что вместо (19) и (20) имеем:

a = aocos(/f) ;

= - оУ sin(/ f f).

Полный период колебания будет равен:

2/- (21)

гр 2п

Точное интегрирование дифер. ур-ия (17) приводит к эллиптическим функциям.

К. д. под действием с и.ты притяжения, пропорциона.тьной расстоянию, и силы, постоянной по величине и направлению. Допустим, что на точку массы т действуют две силы, линии действия которых совпада-