можно пользоваться также следующей ф-лой: L = 2n.D.m [(l + ~ + .) In -F +

где C=Vl -i- (ф-ла Стефана), а F и G показаны на графиках фиг. 10. Спиральные К. с. из круглого провода рассчитываются по формуле:

L = 2nD

m 2 24D \ m 12)

где m = N Ь, a D = a+(n -l)b; значения a и b CM. на фиг. 11.

Спиральные К. с. из проводника прямоугольного сечения (ленты) м. б. рассчитаны по формуле Стефана для плоских галет (см. выше), где I-уисе толщина ленты. Плоские,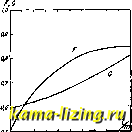

о e,t о 0,3 0,4 0.S 0,в 0,7 0 0 tfi

Фиг. 10.

Фиг. и.

а также и цилиндрические К. с, могут быть рассчитаны по упрощенной формуле, предложенной впервые проф. Шпильрейном []:

L = № D к, где /с определяется по графику фиг. 12.

Сотовые и корзинчатые К. с. рассчитываются лишь с нек-рым приближением по ф-лам цилиндрических, многослойных и плоских К. с.

Тороидальные К. с. рассчитываются по формуле:

L = 2я № {J-УЖ-Щ , где Л-диам. тороида между центрами его сечений, а D-диам. намотки.

ВосьмерочныеК. с. рассчитываются как цилиндрические или многослойные, в зависимости от вида катушки, с учетом коэфициента взаимоиндукции .между катушками, образующими восьмерку.

Расчет самоиндукции многоугольных К. с. может быть приведен к расчету эквивалентной цилиндрической К. с, если воспользоваться поправочными коэфи-

циентами (Грове-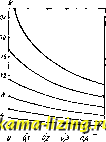

Фиг. 12.

pa), данными на фиг. 13. Для определения I нужно вычислить l:Di и из графиков найти соответствующую величину D : D, где - диам. описанного круга. Отсюда определяется D, и дальше все расчеты сводятся к расчету цилиндрических К. с. Для ускорения и упрощения технич. расчетов К. с. разработан целый ряд таблиц и номограмм, при помощи которых все слолнейшие расчеты

Восьмиугольник

Квадрат

Треальнии

/ CIZ ол O/i < о,е о, аа dfi ио Фиг. 13.

Ь К. с. могут быть произведены в несколько минут с точностью до 5-10% и большей, что для практических целей б. ч. достаточно.

Величины С, Яд к для К. с. Сопротивление К. с. для постоянного тока и очень низких частот определяется активным сопротивлением (постояв- липому току) прОВО- Д , , , Лосдчашугольи.

да, из которого она намотана. При высоких частотах коэфициент самоиндукции и сопротивление К. с. изменяются, причем это изменение вызывается одновременно двумя причинами: собственной емкостью катушек и вихревыми токами.

1) Собствен на я, или распределенная, емкость К. с. для удобства расчетов м. б. представлена в виде нек-рого конденсатора, шунтирующего катушку и эквивалентного суммарному емкостному эффекту между отдельными витками. Величина собственной емкости Cq К. с. обычно невелика. В случае однослойной К. с. она не зависит от числа витков и лишь в незначительной степени зависит от отношения длины к диаметру. При 1-0,Ъ D величина С© приблизительно равна 0,54г- (г-радиус катушки). При 1=2D она равна 0,57 г (Гоу) или также приблизительно равна 7% периметра (Брейт). Со К. с. может быть также охарактеризована собственной длиной волны

Ао = 2я 1/1Г-7?у Величина к. с. (в м) определяется из уравнения До = 2/el (Дру-де), где к-фактор, зависящий от отношения I : Ъ я bid (фиг. 14). Со однослойных К. с. обычно не превышает 10 сж и равна нормально 3-5 см; Со цйлиндрич. корзинок- порядка 2 см; Сд многослойных К. с. значительно выше и достигает 30--40 см. Наибольшую Сц имеет двуслойная К. с; при увеличении числа слоев Со уменьшается. На фиг. 15 показаны кривые зависимости Со от числа слоев для катушки, у которой = 3,8 см, 1=8 см, N (в слое) = 58 виткам. Емкость К. с. вызывает при увеличении

частоты / увеличение действующих L и R. При рабочих длинах волн, близких к Яо. действующий L определяется из уравнения:

Фиг. 14.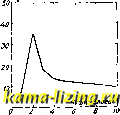

Фиг. 15.

1 с.

Lo{l + vi -Lo Co);

Фиг. 16.

действующее JJ определяется из уравнения

р До 0

д. - (1 со . Ь С.) (1 - л /Л ) -

Ro(l + 2co Lo- Со), где Lf, и -значения при постоянном токе. Таким образ, сопротивление увеличивается с частотой быстрее, чем L. На фиг. 16 показана зависимость R: Rgor А : Яц. Неудовлетворительная изоляция намотки К. с, являющейся диэлектриком для емкости между витками, вызывает дополнительные, т. н. диэлектрические, потери К. с. Проводимость утечки изоляции G увеличивает сопротивление К. с. на величину ДД. - со G; так как G=co Со tg, то

ARI = (о -L- Co-tge, где tgd-угол потерь, вызываемый емкостью К. с. Для наиболее распространенных видов изоляции проволок, применяемых д.71я намотки К. с, tS(5 имеет следующие величины: эмаль-0,018, щеллак-0,04, хл.-бум. изоляция-0,36 (по Штреккеру). Склеивающие катушку составы вызывают обычно дополнительные диэлектрические потери. На фиг. 17 показаны кривые зависимости й от / для одинаковых К. с, но покрытых различными составами. Ко-эфициент самоиндукции-L при диэлектрической утечке остается в первом приближении неизменным.

2) Вихревые токи (токи Фуко). Магнитное поле токов, протекающих в других витках К. с, приводит к аксиальной несимметричности тока в проводнике данного витка, что в свою очередь вызывает увеличение сопротивления R катушки, значительно большее возрастания сопротивления от скин-эффекта в прямом проводе. В то же время вихревые токи вызьшаютумень-шение I/c увеличением частоты. Это уменьшение с частотой может быть определено из уравнения, предложенного Зоммерфельдом:

Фиг. 17.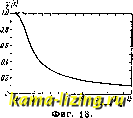

1 - Ч> {X)

3 JD

\ y-Vs.

где ж = iS VZn со а, S-сторона квадрата поперечного сечения провода, у-фактор, учитывающий изоляцию и поправку на круглый провод; обычно у=1,25.

, ч я/ sh2.x-sin23c

(*) = /2Ть2х:2.х-Кривая зависимости (р{х) от ж показана на фиг. 18. Уменьшение L с частотой от вихревых токов обычно компенсируется увеличе-

/. ТОг.

нием I/, вызываемым собственной емкостью К. с. На фиг. 19 показаны кривые зависимости L от /, измеренные для наиболее распространенных приемных К. с. Из этих кривых видно, что уменьшение L с частотой от вихревых токов значительно меньше по абсолютной величине, чем н увеличение h от емкости, поэтому практически К. с. дают обычно увеличение hf. Сопротивление К. с, вызываемое потерями в проводе, м. б. рассчитано по следующим ф-лам, предложенным Бёттеруортсом и хорошо оправдывающимся на практике. Для однослойных К. с:

Rf=R, (l-f F-f wf.-G); здесь F = для низких частот и F = /

Фиг. 19.

где е-

для высоких частот (Z = nd

удельное сопротивление, выраженное в абсо-лютн. единицах), = - для низких частот и

V2Z-1

для высоких частот, г* - зави-

сит от размеров катушки. В табл. 1 даны значения 1-\-F и G для меди ( = 1700).

Т а б л. 1 .-3 начеиия 1+F и G для меди.

64 0,00097 0,01519 0,0691 07810,1724 17510,2949 0,4049 0,4987

11,678

l,863 2,043 2.394 2,743 3,094 3,446 3,799

0,5842]

0.669 0,755 0.932 1,109 1,287 1,464 1,641

20 30 40 50 80 100

>100

5,562

7,328 10,86 14,40 17, V):! 28,54 35 61 )/2-Z+l

2,525

3 5 6 8 14 17

,409 ,177 ,946 ,713 ,02 ,55 Z-1

На фиг. 20 даны значения и для цилиндрических К. с, а на фиг. 21-для плоских К. с. Для многослойных К. с.

.R,-Jf,[l + ir + J(-.).G].

Для К. с. с большим числом слоев величины К даны в табл. 2.

Табл. 2.-Значения коэфициента К.

На фиг. 22 и 23 показаны If для цилиндрич. и плоских К. с. в один и два слоя, а тахске при бесконечном числе слоев. На фиг. 24 показаны кривые R в зависимости от / для тех же приемных К. с., для к-рых на фиг. 19 дана была зависимость L от /.

Для уменьшения сопротивления К. с. применяют т. н. лицендратовый проводник, состоящий из многих изолированных друг от друга жил, скрученных т. о., что каждая жила лежит частью внутри кабеля, частью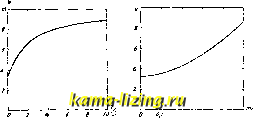

Фиг. 20.

0,2 0.3 0.Л 0,SJJ

Фиг. 21.

на его наружной поверхности. Лицендратовый проводник уменьшает влияние скин-эффекта с последующим уменьшением Rf. Сопротивление К. с, намотанных из лицен-дратового проводника, опреде.тяется ур-ием:

где Uq-диам. жилы лицёндрата, а Пд-число жил в нем. Фактор к зависит от п; его значения следующие:

п ....... 3 9 27 Большое

к........ 1,55 1,84 1,92 2

В табл. 3 показана величина wL : R для катушек (D = 8,3 см, 1=1,5 см, т = 3 см), намотанных сплошным и лицендратовым

б/ аз 03 0, aS Фиг. 22.

0 0,3 OA 0.5

Фиг. 23.

проводниками: при очень высоких частотах лицендратовый проводник теряет свое значение вследствие возрастания диэлектрических потерь между жилами.

Табл. 3. -Значения величины toL : JR.

Наилучшие размеры К. с. К. с. действует тем лучше, чем меньше R при данном Lf, т. е. чем меньше R : L или R : coL. Хорошо сконструированная К. с. для передатчика должна иметь Е : coL 0,002; у приемной К. с. Д : a)L< 0,010,005; R : L обратно пропорционально D. Самая форма К. с. при этом оказывает очень малое влияние на отношение R: L, даже при ее значительных

изменениях. Оптимальная длина К. с. определяется шагом намотки. Наилучший шаг намотки в свою очередь определяется из

соотношения: = /(Z), где Z = (R-

сопротивление постоянному току 1 км данного провода; Л-в м). Кривая зависимости от Z, построенная Бёттеруортсом, показана на фиг. 25. При отклонении на 20% шага намотки от значения, указываемого этой кривой, R : L увеличивается приблизительно на 5%. Для средних частот Z < 2 и отношение l:D д. 6.0,35; для высоких частот Z > 2 и отношение I: D 0,3. В случае многослойных К. с. оптимальнов I: т для низких частот д. б. порядка 1, для высоких частот-порядка 0,3-0,5. В тороидальных К. с. для получения минимального R : L отношение внешних и внутренних радиусов тороида Гг: r-j = 2,66.

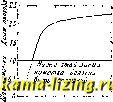Фиг. 24.

0 12 3 UJ S 7 8 S W Фиг. 25.

На фиг. 26 показано изменение величины coL: R для наиболее распространенных видов приемных К. с. (фиг. 19 и 24). Кривые наглядно показывают, что для радиовещательного диапазона наилучшими К. с. являются однослойные. В случае длинных волн для получения минимальных R : L однослойные К. с. пришлось бы строить с очень большим D. Поэто-. му, в целях компакт-ности,в приемниках применяют многослойные К. с; в диапазонах волн 1000- 3 ООО м применяются сотовые К. с, на волнах более высоких-галеты. В передатчиках на всех волнах рационально применять лишь однослойные К. с, 41000 вполне осуществимо, т. к. Ь К. с. в передатчиках дляданных волн невелика, в виду больших емкостей контурных конденсаторов.

При конструировании приемных К.с. вопросом громадной вал-сности является

выбор наивыгоднейшего диаметра провода катушки для получения минимального R : L. Для однослойных и многослойных К. с. наивыгоднейший диам. провода d определяется из уравнения, устанавливающего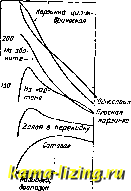

500 1000

Фиг. 26.