Фиг.

звеньев, нагруженных между шарнирами. Для его равновесия необходимо и достаточно, чтобы существовал веревочный мн-к, соответствующий данной внешней нагрузке и обладающий тем свойством, что его стороны проходят через соответствующие вершины дискового мн-ка. Теория равновесия замкнутого дискового коль-ц а автоматически вытекает из теории равновесия дискового многоуголышка как ее частный случай.

Построение линий влияния (инфлюентная линия). Пусть требуется определить линию влияния усилия X в каком-нибудь стержне или связи фермы. Удалим этот стерлгень и заменим его силами X, как показано на фиг. 10; движущийся груз обозначим через Р. Ур-ие работ при возможном перемещении этого механизма молсет быть представлено в виде:

1 Vp - Xvj = О , где -скорость изменения расстояния СБ И.ТИ, в более общей формулировке, скорость того перемещения, на котором работают си-.ты X. Отсюда:

Х = -.

Знаменатель этой дроби, как скорость определенной точки или группы точек соорулсе-.ния, можно считать постоянным, числитель же, по самой природе своей,-переменный. Полученная ф-ла приводит к следующему замечательному выводу: для получения ин-флюентной линии усилия любой связи статически определимой фермы следует удалить эту связь, сообщить образовавшемуся механизму бесконечно малое перемещение и для всех точек сооружения, по которым доллша перемещаться точка приложения груза Р = 1, построить проекции скоростей на направление, параллельное этому грузу; полученная диаграмма скоростей и будет выражать собою в некотором масштабе искомую инфлюенту.

При бесконечно малом перемещении механизма кал-сдое звено его поворачивается около своего мгновенного центра вращения, а скорость любой точки звена пропорциональна ее расстоянию до этого мгновенного центра. Отсюда вытекает следующий ряд важных выводов. 1) Участок всякой ин-ф.тюентной линии, соответствующей движению груза по одному звену механизма, представляет собою прямую линию. 2) Нулевая точка (т.е. точка пересечения с осью абсцисс) каждой из прямых, составляющих инфлюенту, представляет собою проекцию мгновенного центра вращения соответствующего звена по направлению движ:ущейся силы. 3) Точка пересечения двух прямых инфлюенты представляет собою проекцию мгновенного центра взаимн. вращения соответствующих двух звеньев; если последние движутся друг относительно друга поступательно, то обе прямые оказываются

параллельными между собою. 4) Если ось абсцисс инфлюентно!! линииперпендикуляр-на к направлению проекций Vp, то тангенс угла наклона любой прямой к оси абсцисс выражает собою в выбранном масштабе угловую скорость вращения соответствующего звена относительно неподвижного; этот угол следовательно не зависит от направления ординат Vp.

Эти основные теоремы вполне достаточны для построения любой статически определимой инфлюентной линии. Они же позволяют с недостижимой для друг, методов наглядностью сразу, без каких-либо предварительных вычислений, представить себе весь характер и очертание инфлюентной линии, а также проверять результаты построений, сделанных друг, способами. Масштаб ординат инфлюенты показан на фиг. 11. Для определения усилия в стержне J-S, соединяющем два звена, находим мгновенный центр. Oig взаимного вращения этих звеньев и опускаем из него перпендикуляр г на стержень АВ; любая ордината d, заключенная мелоду прямыми 1 я 2, выражает собою проекцию vp относительной скорости под грузом и следовательно выражается формулой d = ; на расстоянии г от

точки М инфлюентной линии отрезок ординаты между прямыми .7 и5 доллен быть равен единице. Отсюда следует, что ординаты продолжения прямых, проведенных через мгновенные центры 13 и 23 вращения этих звеньев относительно неподвижного, имеют показанные на чертеже величины я . При

построении инфлюентной линии момента следует принимать г = 1. Повернем звенья

Фиг. 11.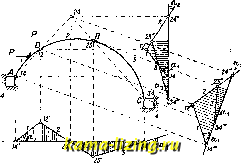

Фиг. 12.

1 Я 2 на фиг. 11 так, чтобы сила Р, стоящая в какой-либо точке, совершила положительную работу. Если при этом расстояние АВ увеличится, то ордината под этой точкой полонштельна-таково правило знаков.

На фиг. 12 показано кинематическое построение инфлюентных линий изгибающего момента в сечении D трехшарнирной арки АБС при трех различных направлениях движтцегося груза; равные углы обозна-

чены на всех трех инфлюентиых линиях одинаковыми буквами. Для построения всех этих инфлюент достаточно найти мгновенный центр 54, к-рый лежит на пересечении прямых AD и СВ. На фиг, 13 показано построение инфлюентиых линий для различных стержней балочной фермы при помощи мгновенных центров вращения; все масштабы выписаны на чертеже. На фиг. 14 показано применение неполярного плана ско- ростей для той же цели. Части а и б фигуры представляют собою инфлю-ентные линии усилия в раскосе JD соответственно при yj езде понизу и поверху; заштрихованное же звено считается неподви-лшым. Изображение 4 точки 4 помещаем в точке 2; изображения всех остальных узлов строятся без всякого труда; как видно по надписям, целый ряд изображений совпадает между собой. Сближение точек 4 п 1 выражается проекцией вектора dd на направление, перпендикулярное к D, т. е. v- sin 99, где Л-длица панели и (р-угол наклона раскоса I) к поясу. Отсюда получаем масштаб: Я sin <р = 1.

Вертикальная скорость Vp точек 5, 9, 13 равна бУ = 99 = 13 ~ 13 = А = . - . В точ-

sin д>

ке А получаем ординату 16 -16 =

В остальных узлах ординаты инфлюенты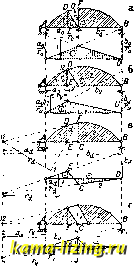

Фиг. 13.

равны нулю. Т. о. получается зигзагообразная инфлюента (фиг. 14, а), у которой крайняя правая ордината равна нулю, а крайняя левая = 2sE - После этого изменяем неподвижное звено, для чего достаточно провести ось абсцисс так, чтобы крайние ординаты обратились в нуль.

Применение кинематики к решению статически неопределимых задач. Простейшее применение заключается в определении линейных

перемещений узлов и узловых перемещений стержней в рамных сооружениях. Для решения этой задачи следует поместить во всех без исключения узлах сооружения шарниры, считать все стержни абсолютно леесткими и для полученной т.о. кинематич. цепи построить план скоростей. Если цепь имеет п степеней свободы, то следует взять п независимых друг от друга возможных перемещений и для каждого из них построить отдельный план скоростей. Из этих планов и определятся графически линейные и узловые перемещения, фигурирующие в статически неопределимой задаче при решении ее по методу деформаций.

Другое более важное применение заключается в чисто графическ. решении статически неопределимых рамнхх сооружений. По известной теореме Мора, перемещение любой точки стерлепя по .любому направленхпо м. б. представлено как изгибающий момент от фиктивной нагрузки, выражаемой эпюрой -gj , где М-действР1тельный изгибающий момент в любой точке. Эта фиктивная нагрузка должна считаться приложенной к каждому элементу ds по его оси и иметь направление, параллельное интересующему нас перемещению. С изменением направления перемещения необходимо соответственно переменить и направление всех фиктивных сил.

Фиктивная нагрузка действует на ф и к-т и в н о е соорулеенне: в неподвижной точке данного соорулсения фиктивный изгибающий момент равен нулю; в неподвижном (защемленном) сечении фиктивная поперечная сила равна нулю. Фиктивное сооружение, получаемое на этом основании, имеет шарниры в точках, соответствующих неподвижным точкам действительного со-орулгбиия, и свободные концы-в защемленных концах действительного сооружения. Построение эпюры моментов сводится к уравновешиванию фиктивной нагрузки на фиктивной кинематич. цепи или на фиктивном дисковом мн-ке.

Лит.: Рабинович И. М., Кинематич. метод в строит, механике в связи с графич. кинематикой и статикой плоских цепей, М., 1928.

Тимошенко СП., Курс статики сооружений, Л., 1926,- П р о к о ф ь е в И. П., Теория сооружений, ч. 1, М., 1926; Мюллер-Бреслау Г., Графич. статика сооружений, т. 1, пер. с немецкого, 2 изд., стр. 391-4,53, СПБ, 1908. И. Рабинович.

КИНЕТИКА ХИМИЧЕСКАЯ, отрасль теоретич. химии, изучающая скорости химич. реакций. В основе опытной методики этого изучения лелеит определение концентрации прореагировавшего либо появляющегося вещества в функциональной зависимости от времени. Различают кинетику о б-ратимых и необратимых реакций. К необратимым относятся те реакции, к-рые практически протекают лишь в одном направлении; это имеет место в случаях, когда продукты, к-рые образовались в результате химич. процесса, удаляются из сферы реакции и тем самым лишаются возможности обратного взаимодействия, или когда, обрат-пая реакция протекает лишь с незначительной скоростью. В случае обратимых реакций продукты вступают между собой во взаимодействие, давая исходные вещества; при

этом результирующая скорость определяется как разность скоростей прямой и обратной реакции. Далее, различают кинетику гомогенных реакций, протекающих в одной фазе (напр. когда все участвующие в реакции вещества газообразны), и гетерогенных, протекающих в разных фазах. К последним относятся реакции, сопро-волсдающиеся образованием газообразных продуктов из твердых, переходом твердых веществ в раствор и т. п. Строго гомогенных реакций известно весьма мало; детальное исследование часто обнаруживает, что т. н. гомогенные реакции протекают на стенках сосуда и что их течение зависит от материала сосуда, а также от примесей твердых веществ, на поверхности к-рых может происходить адсорбция или, в общем случае, такое изменение свойств, которое делает молекулы активными, т. е. реакциеспособны-ми (см. Катализ).

Скорость реакции зависит от числа столкновений соответствующих молекул, поскольку химич. силы проявляются лишь на расстояниях порядка молекулярных размеров (Юсж). В связи с этим основная закономерность К. x. меняет быть выражена так: скорость реакции, т. е. убыль первоначального (или прибыль конечного) вещества во времени (или, иначе, производная концентрации по времени) пропорциональна числу столкновений наличных молекул. Согласно кинетич. теории, число столкновений п различного рода молекул пропорционально общему числу молекул в п-ной степени. Если реакция протекает по ур-ию:

nA + mBD-h ...

и если к моменту времени t концентрации молекул А, В я В соответственно равны Ci, Сз и Сз, то скорость реакции v выра-лсается ур-ием:

Ур-ие (1) показывает, что скорость реакции с течением времени уменьшается по мере уменьшения числа молекул А я В. Постоянной величиной, независящей от концентрации,является fci-к онстанта скорости реакции. Только изменение энергетич. условий, например повышение Г, влияет на величину fci.

В зависимости от того, сколько молекул должно столкнуться для элементарного акта взаимодействия, различают реакции 2-го, 3-го и т. д. порядков. Известны однако случаи, когда нельзя сде.тать непосредственного вывода о необходимости столкновений д.тя осуществления реакции и когда элементарный акт реакции заключается как бы в самопроизвольном распаде молекулы. Классическим примером такого процесса является распад NjOg, причем скорость реакции пропорциональна наличной концентрации данного вещества в первой степени и в значительных пределах не зависит от примесей посторонних газов. Если начальная концентрация равна С, а ко времени t прореагировало количество вещества х, то

[ = /е,(С-ж), (2)

я; = С(1-е-*1). (3)

В случае, когда для реакции необходимо п столкновений, уравнение(2) приобретает вид:

= К{С-х)- (4)

[\.{п-\)кС

in - 1

Наблюдая течение реакции во времени, находят путем подбора такое значение для п, при к-ром концентрация, как ф-ия времени, выралсается ур-ием вида (5) при постоянном /с. Так. обр. находят порядок химич. реакции. Опытные исследования показывают, что реакции высоких порядков весьма редки. Это находит себе объяснение в том, что одновременные столкновения большого числа молекул мало вероятны и происходят гораздо реже, чем парные или тройные соударения. Много реакций протекает по ур-иям кинетики 1-го и 2-го порядков.

Исследование скорости реагщий позволяет выяснить их механизм. Обычное стехиоме-трич. ур-ие реакции означает только баланс начальных и конечных веществ, составленный так, чтобы зная-чтб реагирует и чтб получается, подобрать такие коэфициенты, при к-рых выполняется закон сохранения материи. Однако нет веских оснований для предположения,что реакция протекает именно по написанному ур-ию. Определяя кинетически порядок реакции, исследуя влияние избытка разных комнонентов ее, выясняют механизм реакции и характер элементарных актов, в результате к-рых появляются новые молекулы. Весьма часто слолные реакции осуществляются через образование промежуточных веществ, обладающих небольшой длительностью существования и превращающихся при помощи цепи промежуточных реакций в конечные продукты. Каждая промежуточная реакция идет со своей специ-фич. скоростью. Измеряемая общая скорость реакции определяется течением наиболее медленной промежуточной.

К. x. в растворах осложняется ролью рас-творите.чя, влияющего на константу скорости. В этой области известно весьма мал© систематических исследований. Для типичного случая образования йодист, тетраэтил-аммония, N(C2H5)4J, найдено возрастание константы скорости с увеличением диэлек-трич. постоянной растворителя. Последнее свойство находится в связи с ионизирующей способностью растворителя.Допущение, что каждое сто.лкновение соответствующих молекул ведет к реакции, требует, чтобы последняя протекала с очень большой скоростью. Это оправдывается для ионных реакций. В большинстве случаев однако лишь незначительная часть столкновений эффективна. Исследование влияния Г на скорость реакций подтверждает указанную точку зрения. Небольшое повышение t°, примерно иа 10°, влечет за собой увеличение константы скорости в 2-3 раза, тогда как число столкновений при этом растет весьма незначительно (пропорционально УТ). Теория приводит к следующему соотношению мелоду