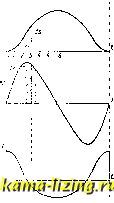Фиг. 4.

валам и составляют первую диаграмму s, t (фиг. 4). Графическим диференцированием с этой диаграммы снимают приращения ds за каждый интервал времени dt. Отношение

= в выбранном масштабе откладьшают

в средине интервала как среднюю скорость и так. обр, получают вторую диаграмму v, t.

Из этой второй диаграммы аналогичным способом снимают приращения dv3Si каждый интервал времени и составляют третью диаграмму j, t. Нулшо заметить, что при криволинейном двилсении точки мы можем получить описан, методом не полное ускорение точки, а только тангенциальную составляющую его. Во многих случаях этого бывает достаточно. Если же требуется знать полное ускорение по величине и по направлению, то пользуются методом планов скоростей и ускорений. Обратная задача состоит в графическом интегрировании. Она заключается в следующем. Изг; = следует,

чю8 = Jvdt. Таким образом путь точки за

известный промежуток времени является площадью на графике скоростей за этот промежуток. Измеряя эту площадь, напр. при помощи планиметра, получим путь s. Этим приемом хорошо пользоваться в том случае, когда скорости движения точки заданы, а требуется найти перемещения ее. Подобным же образом из ускорений получаются скоро-

сти; именно: ? = ~у , откуда v=- J j dt,H сле-

довательно площадь на графике ускорений соответствует скорости точки. Планы скоростей и ускорений строятся графич. приемами на основании геометрич, соотношений, которые устанавливаются между векторами скоростей и ускорений разных точек механизма, Т. к, при построении планов скоростей и ускорений наряду с графич. построениями продельшается значительная вычислительная работа, то метод этот следует считать графо-аналитическим.

Кинематическое исследование передач охватывает собой учение о передачах: фрикционной, зубчатой, гибкой связью, кулаками и эксцентриками, а также стержневой пространственной и в частности шарниром Гука. У всех этих передач устанавливают отношение скоростей меледу <Л1:епленными деталями; кроме того находят форму правильно построенных очертаний зубцов зубчатых колес, кулаков и эксцентриков. Обратная задача состоит в том, что по данной форме этих деталей определяют закон движения.

т. Э. т. X.

Лит.: 3 е р н о в Д. С. Прикладная механика, Л., 1925; Левенсон Л. В., Кинематика механизмов, М., 1923; М е р ц а л о в Н. И., Кинематика механизмов, М., 1916; Р а д ц и г А. А., Прикладная механика, М.-П., 1923; Рузский Д. П., Кинематика машин, Ленинград, 1924; Смирнов Л. П., Кинематика механизмов и машин, М.-Л., 1927; Столяров Я. В., Теория механизмов, Харьков, 1926; А с с у р Л., Исследование плоских стержневых механизмов с точки зрения их структуры и классификации, ч. 1, СПБ, 1914, ч. 2, П., 1915; Малышев А. П., Анализ и синтез механизмов с точки зрения их структуры, Томск, 1923; его же, Прикладная механика, вып. 1-Структура и синтез механизмов. Томск, 1923; Кирпичей В. Л., Построение путей, описываемых точками плоского механизма, Собр. сочинений, т. 1, П., 1917; его ж е, Построение картины скоростей и картины ускорений для плоских механизмов, там нее; А с с у р Л. В., Картины сно-ростей и ускорений точек плоских механизмов, СПБ, 1911; А л ь б и ц к и й В. И., Цилипдрич. зубчатые колеса, их теория, расчет и вычерчивание, 2 изд., Харьков, 1892; Б е р л о в М. П., Детали машин, Сокращ. руководство по расчету и проектир., ч. 1-2, 2 изд., М., 1929; М а л ы ш е в А. П., Передача гибкой связью при некруглых шкивах, Изв. Моск. текстильного ин-та , М., 1928; Burmeister L., Lehr-buch d. Kinematik, Lpz., 1888; BouasseH., Theorie des vecteurs. Clnematique des mcanlsmes. P., 1921; Heck R. C, Mechanics of Machinery. Mechanism, N. Y., 1923; G r ii b 1 e r M.. Lehrbuch d. technischen Mechanik.B. 1-3, В., 1921; Ham C. W. a. С r a n e E. J Mechanics of Macliinery, N. Y., 1927; R e n-leaux F., Theoretische Kinematik, B. 1, Brschw., 1875, B.2, Brschw., 1900; Grubler M., Getriebelehre, В., 1921; .S t r i b e с к, Versuche mit Schneckengetrie-ben, Z. d. VDr , 1897; Flanders R.. Gear-Cutting Machinery, N. Y., 1910; В u h 1 e, Der Renolds Ketten-trieb, Gluckauf , Essen, 1904; Buckingham E.. Spur Gears, N.Y., 1922; Hi scox G., Mechanic. Appliances. Mechanical Movements, 5 ed., L., 1925; Brown H., Bewegungsmechanismen, Ipx., 1925. A. Малышев,

КИНЕМАТИЧЕСКИЙ МЕТОД в строительной механике, применение прин-inina возмол-сных перемещений к решению вопросов теории сооружений; в более узком смысле-применение этого принципа к определению усилий в шарнирио-стерленевых фермах от действия неподвижной и подвижной нагрузок. Основная идея К. м., разработанного гл. обр. трудами Мюллера-Бре-с.тау и Мора, состоит в следующем: путем удаления одной или нескольких связей сооружение обращается в кинематическ. цепь, имеющую одну или несколько степеней изменяемости; искомые свойства сооружения получаются из рассмотрения свойств дви-леения и условий равновесия этой цепи.

В настоявшей статье рассматриваются ис-к.лючительно применения кинематики к плоским сооружениям. Применение кинематики к сооружениям пространственным разработано пока очень мало.

Поверка неизменяемости со о руле е н и й. Необходимое условие статическ. определимости и неизменяемости сооружения заключается в том, что кинематич. цепь, получаемая из сооружения при удалении каких-либо связей, долнепа иметь степень свободы, равную числу этих удаленных связей (стержни сооружения считаются абсолютно леесткими). Отсюда выводится соотношение между числом стержней С и числом шарниров Ш шарнирно - стерленевой плоской статически определимой и неизменяемой фермы: 2Ш - С = О (.здесь С-полное число стерлгней, включая и опорные). Отсюда же можно вывести и соотношение меледу числом звеньев (неизменяемых систем) п и приведенным числом шарниров р любого плоского статически определимого сооружения:

Зи - 2р -3 = 0:

приведенное число шарниров получается, если каждый шарнир, соединяющий г звеньев, считать за г -1 простых шарниров.

Всякое сооружение, статически определимое, неизменяемое и неподвилшое в общем виде, может, при нек-ром специальном подборе длины стерлшей, потерять свою неизменяемость или неподвижность, т. е. превратиться в кинематич. цепь. Если эта цепь допускает лишь бесконечно малые перемещения, соорулгсние называется мгновенно изменяемым. Мгновенно изменяемое сооружение непригодно для практ. целей, так как от действия ничтолно малых внешних нагрузок в нем могут возникать большие деформации и большие внутренние усилия. Система уравнений статики, которая служит для определения всех усилий и реакций такого сооружения, имеет детерминант, равный нулю, и поэтому получает решение неопределенноеили бесконечное. Мгновенная изменяемость вскрывается проще всего К. м.: нужно удалить одну связь, рассмотреть возможное перемещение полученного механизма и выяснить, противоречит ли удаленная связь этому перемещению; если противоречия нет, то данное сооружение несомненно обладает мгновенной изменяемостью.

На фиг. 1 показана неизменяемая фигура, обозначенная цифрой 1 и опирающаяся на неподвижную систему 5 при помощи опорных стержней 2, 3 а и 4. Удалив один из --- стержней, получим /. мгновенный центр вращения звена 1 в точке пересечения

остальных двух Ojg; в том случае, когда все три стержня пересекаются в одной точке, движение (бесконечно малый поворот звена 1 вокруг точки Ois) оказывается возмолсным и при наличии всех трех опорных стержней. Свойство мгновенной изменяемости сохраняется и в том случае, когда три стержня, пересекающиеся в одной точке, служат для взаимного соединения каких-либо двух неизменяемых частей сооружения, как это 1]31збро.жено например на фиг. 2, где соединительные стержни пересекаются по три: в точках Н п I. Случай параллелизма трех соединительных стержней должен рассматриваться как частный случай пересечения трех стерлней в одной точке.

Если какие-либо два звена (обозначим их цифрами 1 и 2) или два стерлсня соединены менеду собой шарниром, то разъединив звенья в этом шарнире, получим два механизма и в каждом из них ьшйдем мгновенный центр вращения одного из названных звеньев относительно их общего звена; если шарнир и эти два мгновенных центра лежат на одной прямой, то даииое сооружение мгновенно изменяемое. На фиг. ;3 точкам, играет роль мгновенного центра 17 (т.е. звена 1 относительно звена 7), точка С-центра 27. следовательно соорулсение является мгно-

Фиг. 2.

венно изменяемым. Из этого примера следует, мелоду прочим, что трехшарнирная арка с шарнирами, распололченными по одной прямой, мгновенно изменяема.

Для раскрытия мгновенной изменяемости пользуются также планами скоростей. Если по удалении какого-либо стержня сооружения можно построить план скоростей (изобра-лающую фигуру), все линии КО! орого параллельны соответствующим стержням данной цепи (в том числе и уда-лепному стержню), то сооружение мгновенно изменяемо; в противн. случае-неизменяемо. Теорема одинаково справедлива при пользовании полярным или ненолярным планами скоростей. Пример такого решения задачи показан на фиг. 4, в применении к ферме

Фиг. 3.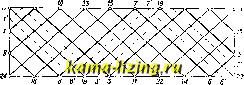

Фиг. 4.

Мертенса, имеющей один лишний стерлень и тем не менее мгновенно изменяемой. Пунктирный зигзаг представляет собою неполярный план скоростей и изображает такое перемещение, при котором узлы изображаемого зигзага перемещаются, в то время как остальные узлы остаются неподвижными.

Кинематический способ определения усилий от неподвижной нагрузки представляет собою непосредственное применение статики механизмов и многократно изменяемых кинематич. цепей (т. е. цепей с большей степенью свободы, чем у механизма). Основные теоремы статики механизмов, вытекаюшие из принципа возможных перемещений, наиболее удобно выралгаются при помощи полярных и неполярных планов скоростей. На неполяр- А ном плане каждая точка А механизма (фиг. 5, а) изображается в виде нек-рой точки А, а каждая прямая АВ, не изменяющая своей длины во время двилсения.- некоторой прямой АВ\\АВ. Скорость или перемещенкр любой точки А выражаете, в одном и том же (прои;;-вольном) масштабе вектором А А; направление перемешс-пия перпендикулярно к этому вектору. При равновесхш механизма сумма статических моментов всех внешних сил относ11тельно точек, которые служат изображениями точек приложения соответств. сил, равна нулю. На полярном плане скоростей (или перемещений)

Фиг. 5.

изображение а каждой точки А получается (фиг. 5, б) как конец вектора Оа, проведенного из постоянной точки О-полюса плана скоростей-перпендикулярно к перемещению точки А; свойство параллелизма неизменяемой прямой АВ и ее изображения аЪ сохраняется и здесь. Условие равновесия механизма: сумма статическ. моментов всех сил, перенесенных на план скоростей, относительно полюса О равна нулю. Иными словами, если мы примем план скоростей за одно звено, имеющее неподвижную точку вращения в полюсе плана и нагруженное всеми перенесенными силами, то это звено окажется в равновесии. Если в числе нагрузок имеется сосредоточенная пара с моментом М, действующая на какое-либо звено АВ (фиг. 5, а), то при пользовании неполярным планом нужно ввести в упомянутое выше ур-ие статических моментов выражение М il - Vl ) > где отношение -- положительно при одинаковом течении

векторов АВ и А В и отрицательно при взаимно противоположных направлениях. При пользовании полярным планом следует

вводить выражение причем дробь

положительна при одинаковом течении векторов аЪ и АВ .

На фиг. 6 показана ферма, для которой обычное построение усилий (без замены стерлсней) затруднительно. Кинематическое построение состоит в следующем: удаляем стержень CD, заменяем его двумя равными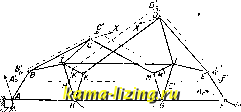

,р.

Фиг. 6.

и противоположными силами X и строим неполярный план скоростей, приняв за неподвижное звено стерЖень IL. Ур-ие равновесия будет иметь вид:

PiH + F + + F +

+ Хкс + Xkjj = О , где kjj-плечо силы относительно точки Я и т. д. и где сумма моментов берется конечно алгебраически. После того как сила X будет найдена, усилия во всех остальных стержнях легко найдутся обычным путем.

На фиг. 7 изобралеена трехъярусная рама, состоящая из трех шарнирных арок, поставленных одна на другую. Требуется определить изгибающий момент в сечении от действия горизонтальной силы. Вставим в сечении F звена ВС шарнир, превращающий иолуарку ВЕС в два звена, и нагрузим это еечение двумя моментами, равными Ж. Построив неполярный план скоростей, показанный пунктиром, получим:

р.т-м(1-55) + м(1-5) = о,

откуда

Р- КК

BF BF

На фиг. 8 показан полярный план для того же механизма; он состоит из одного тр-ка, так как в одной вершине / сливается изображение многих точек. Уравнеьие равновесия имеет вид:

P-Of+Mj-M.

о , или М

1-г-ч-- / / \ \

Фиг. 7.

с.с:

РО/ ~J>1 fc BF FC

Кроме механизмов можно пользоваться также двукратно изменяемыми кинематич. цепями, основываясь на следующих свойствах таких цепей: 1) при всевозможных бесконечно Д1алых перемещениях цепи геометр, местом мгновенных центров взаимного вращения каких-либо двух звеньев служит прямая; 2) если в системе, имеющей две степени свободы, задано направление скорости какой-нибудь точки А, то, при воз-молгных перемещениях этой системы, изображения всех ее точек на полярном и неполярном планах скоростей перемещаются по прямым линиям. Удалив из сооружения две связи, рассматривают два различных возмолс-ных перемещения получен, цепи, строят для каждой из них план скоростей и приходят к вышеуказанным уравнениям равновесия. Из этих двух уравнений и определяются усилия в обеих устраненных связях. Легко подобрать два таких движения, при к-рых в каждом уравнении остается лишь по одному неизвестному.Пользование двукратно изменяемой цепью оказывает большие услуги при решении особо сложных по своей геометрической структуре сооружений. Тот же принцип приводит к пользованию многократно изменяемыми кинематическ.цепями, т. е. цепями, обладающими п степенями свободы, где п>2. Нулшо лишь, чтобы п возможных перемещений, для к-рых строятся планы скоростей и прилуняются уривнения равновесия, были все независимыми друг от друга (т. е. чтобы ни одно из них не было линейной функцией остальных),

л-7b

Частным случаем многократно изменяемой кинематической цепи является веревочный многоугольник, теория которого общеизвестна. Обобщением веревочного мн-ка является дисковый многоугольник (фиг. 9), состоящий из