Главные оси. Уравнение центральных кривых имеет следующий вид:

а Х + 2ayXY + aY + Ьзз = О . (4) При повороте осей координат на угол а, т. е. при замене

Х = х cos а -у sin а, Г = ж sin а у cos а получаем:

(ац cos- а + 2ai2 sin а cos а + а.. sin- а) x + + 2 [(аза - sin а cos а + а (COS а - - sin а)]ху +(ai3isin2a - - 2ai2 sin а COS а + cos a) 2/ + bgg = 0 . (5) Выбирая a так, чтобы коэф. при ху равнялся нулю, т. е.

tg2a = --iv-,

11 - 22

МОЖНО привести ур-ие (4) к виду:

ЬпХ + Ь у- + Ь==0, (6)

кроме случая aii=a2a и 12=0, когда tg 2а, а следовате.чьно и а неопределенны; но в этом случае само ур-ие (4) имеет вид: a (X + Y) + b = 0. Последнее есть ур-ие круга. Итак всегда существуют перпендику.тярные направления осей координат, при к-рых ур-ие центральных кривых имеет вид (6); эти направления называются главными; диаметры, лежащие на главных направлениях, называются главными осями кривой. Для круга .тюбые направления являются главными и .чюбая пара перпендикулярных диаметров стужит главными осями. Г.тавные оси об.та-;1;ают замечательным свойством, к-рое легко усмотреть из ур-ия (6): каждая из осей делит хорды, параллельные другой оси, пополам. Это свойство носит название сопряженности. Всякие два диаметра центральной кривой, делящие хорды, параллельные другому, пополам, называются сопряженными диаметрами. Каждая центральная кривая имеет бесчисленное множество пар сопряженных диаметров, вообще не перпендикулярных. Диаметры сопряженные и перпендикутярные-суть главные оси.

Если ЪззФО, ур-ие (6) легко привести к одному из трех видов:

4. ! 1 У

) 8 к

где а и Ь-действительные числа. В первом случае имеем эллипс, во втором гиперболу и в третьем мнимую кривую 2-го порядка, т. к. при действительных х я у сумма двух квадратов не может равняться -1. При bs=0 кривая (6) распадается на пару действительных или мнимых прямых. Мы впдим т. о., что центральные кривые 2-го порядка, кроме мнимой кривой и спустя распадения, дают К. с. (см. Эллипс я Гипербола). Если

Л = О, т. е. = 1/ 11 ]/а22 1 кривую (1) нельзя привести к виду (4). Поэтому делаем поворот осей сразу для ур-ия (1). Коэф-ты при старших членах будут те лев. что в уравнении (5). Подставляя аз = V<-hi К 22. получаем:

(УауСО а -Ь Va.22 sin а)- х- + 2 {Va2 sin а + -Ь Уйуу cos a) (Va22 cos а - Уа sin а) ху + И- ( Vay sin а - Va22 cos а)- у- -f--f 2b,3 ж -Ь 2b23 у + = 0. Выбирая а так, чтобы коэф. при ж равнялся

нулю, т. е. tg а = - , получим, что и коэф. при ху обратится в нуль, и ур-ие примет вид: 22 2/ + 2Ь,зЖ-Ь 2Ь2з2/+ 33 = 0 (7)

13

(см.

Если центр кривой неопределенный выражения для х, у о), то

12 23 ~ 22 13 ~ О!

Т. е. bi3=0. Ур-ие (7) примет вид:

22 У + 2b23 у -Ь 33 = О,

где у и б-1сорни ур-ия (8). Получаем пару прямых, параллельных оси ж, совпадающи: в случае у=й. Если центр кривой в бесконечности, то bi30. Перенося начало координат в точку на самой кривой (7), можно уничтожить свободный член; выбираем эту точку так, чтобы при этом исчез и коэф-т при у; х=--Х+Хо; y = Y+y\; ур-ие (7) примет следующий вид:

Ь22 + 263 + 2 (622 У о + Ьгз) Y + Ь22 ?/6= + -f 2bi3 ж -f- 2b23 2/0 + 33 = О-Достаточно решить систему ур-ий f 62. ув+ Ьгз = О

22 У + 2bi3 Ж + 2Ь.2з + 33 = О

чтобы достигнуть этой цели. Ур-ие (7) примет вид:

Ь22Г2-Ь2Ь1зХ = 0,

= 2рХ,

т. е. получим параболу. Точка (Жо, 2/0) есть вершина параболы, ось X-ось параболы. Итак получай А =0 приводит, кроме счучая распадения на пару параллельных прямых, к К. с. (см. Парабола).

Поляра и касательная к К. с. Четыре точки , Ь,с, d, лежащие на отрезке. называются гармоническими, если аЬ ad be ~ dc

где ab, be, ad, dc-длины соответствующих направ-ченных отрезков. Задавая три точки, всегда, можно найти четвертую гармоническую. Если b-середина отрезка ас, четвертая гармоническая d лежит в бесконечности. Во всех остальных случаях она лежит в конечной части прямой. Для нахождения 4-й гармонической можно реишть ур-ие (9), или применить геометрич. построение, как указано на фиг. 2 (на основании свойств полного четырехугольника). Строя Д.ТЯ каждой секущей прямой из точки M(Xq, Уо) на плоскост1г четвертую гармоническую относительно Ж и двух точек пересечения секущей с кривой (1), по.тучим геометрическое место Ч(твертых гармонических-прямую линию PQ, называемую полярой точки М; точка М- полюс по отношению к ноляре (фнг. 3). Ур-ио поляры имеет вид:

лЖЖо + 12(Ж?/о + УХо) -Ь 222/,/о + 1з(ж + Ж(,) + + 2з(?/ + Уо) + 33 = 0. (10)

Фнг. 2.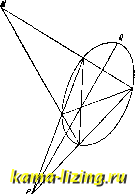

Фиг. 3.

Если из двух точек одна лежит на поляре другой, то и другая лелшт на поляре первой,

или иначе: если из двух прямых одна проходит через полюс другой, то и другая проходит через полюс первой. Это свойство, которое называется полярной сопряженностью точек и прямых относительно К. с, легко усмотреть из С1гмметрии ур-ия (10) относит, точек (х, у) и (Жо, у о). Поляра точки (Xq, г/о), лежащей на самой кривой, есть касательная к кривой в этой точке. Ее уравнение имеет вид (10) при условии, что Хо и Уд удовлетворяют ур-ию (1).

Лит.: Власов А. К., Курс высшем математики, т. 1-Аналитич. геометрия, диферепц. и иитегр. исчисление, ч. 1, М.-Л., 1925; М л о д з е е в с к и й Б. К., Основы аналитичес1;01: геометрии на плоскости, М., 1924; С а л ь м о н Ж., Курс аналнтическоп геометрии двух измерении (конич.сечения), пер. с (Мранн.; Москва, 1908. Ю. Рожанская.

КОНКРЕЦИИ, стяжения, образования в земной коре, происходящие от концентрации различных веществ из растворов в пористых горных породах. Эти стяжения принимают больщей частью сферическую, эллипсоидальную, а иногда гроздевидную и ветвистую формы. Состоят они из самых разнообразных минералов: гипса, роговика, ящмы, углекислой и фосфорнокислой извести, бобовой руды (бурый железняк), барита и др. Центром кристаллизации для стяжений чаще всего бывают тела органические (раковины, тела рыб и т. п.). Иногда внутри К. образуются пустоты от сокращения пли высыхания массы, составлявшей ядро стяжения. Эти пустоты иногда бывают выполнены кристаллами кальцита, кварца, барита, стронцианита, цинковой обманки, свинцового блеска и других минералов. Кроме общего названия существуют специальные названия для некоторых типов К.: и м а т р о в с к и е камни (Финляндия), лаукаские камни (Моравия), очковые конкреции (Египет), н ё к к е р-б р о д (Швеция), к у н к у р с (Индия и Нил), лсуравчики (известковые К. в лёссе). Конкреции встречаются в осадочных породах: известняках, мергелях (известковые К.), глинах, сланцах, песчаниках и т. п. Иногда К. цементируются глинистой массой, что придает лм сходство с брекчией (см.).

К. образуют иногда прослои полезных ископаемых (к о и к р е ц и о н и ы е мест о-рожден и я). Наиболее существенные из них следующие: 1) Дерновые и болот н ы е руд ы леелеза северных районов (Север СССР, Швеция, Норвегия, Финляндия) с влазкиым климатом и заболочеин1л-ми равнинами образуются при выветривании горных пород, концентрируются под дерном кли на дне болот, озер, иногда при участии микроорганизмов; содерлеание Fe в них-от

Т. Э. т. X.

35 ДО 40%. 2) Л а т е р и т о в ы е железняки встречаются в жарких, но не с очень влажным климатом странах: острова Борнео, Минданао, Куба. Месторождение на о-ве Кубе размером 4x9 км с запасом руд в 1 млрд. т разрабатывается открытыми работами. 3) Углистые или глинистые леелезняки каменноугольных месторождений переслаиваются со слоями угля и попутно с ними разрабатываются (Англия, Шотландия). 4) С ф е р о с и д е р и т ы образуются К. РеСОз караваеобразной формы среди осадочных пород.5) Базальтовые железняки Фогельсберга в Германии образовались в результате разрушения покрова базальта. Руды содержат 35-43% Fe, 0,8-1,2% Мп, 0,2-0,8% Р. Добыча-от 600 до 700 тыс. т в год. 6) Марганцевые руды (преимущественно пиролюзит) Ниие-не-Тагильского округа на Урале и Рейнских провинций в Германии, сопутствуемью бурым леелезняком, концентрируются на неровной поверхности известняков, доломитов.

7) Серныйколчедан (пирит, марказит) юрских и каменноуго.тьных месторождений (Подмосковный и Донецкий угольные бассейны, Боровичский р.) разрабатывается попутно при добыче угля или собирается по долинам рек после половодья (река Мета).

8) Медистые песчаники залегают на восточных склонах Урала. 9) Фосфориты юрские и верхнемеловые рассеяны в породе, а также встречаются в виде прослоев и плит. J0) Ванадиевые и урановые руды встречаются в месторождении Тюя-Муюн в Фергане и в штатах Колорадо и Утах США.

Лит.: Самойлов Я., Месторождения серного колчедана в России, П., 1916; Г а е в с к и й П., Железные озерные руды Олонецкого края и их использование, 11ро113ьодите.т!ьные силы района Мурманской ж. д. , П., 1923; Todd J. Е., Concretions а. their (Jeolog. Effect ВнИ of the Geo]. Soc. of America*, N. Y., 1903. 14; Simons II., Zur Kenntnis der oberhessischen Basalteisensteine, Zeits(hrift fur praktisciie Gcologii llalP-. 1919 S, p. 140-147; Berg G. Die Entstehung d. sedimenturen Eisenerze, Geol(jgische Rundscliau* Berlin, .9:4, Jg. 15, p. 97- 1)0; N e w h о u s e W , H,. Some Forms of Iron Sulphide, ,Iournal of Geology*, Chicago, 1 927, v. 35, p. 73-83. H. Федоровский.

КОННЫЙ ПРИВОД, приемник силы живых двигателей (лошади, вола и т. д.), при помощи которого приводятся в двилеение машины. К. п. в сельском хозяйстве применяются для молотилок, соломорезок и мельниц, релее для насосов, камнедробилок и других машин. К. п. бывают главным образом двух типов: 1) с круговым движением рабочих леивотных, припрялеенных к водилу, и 2) т о п ч а к и с нагелонно поставленным бесконечным полотном, на которое ставится упряжное леивотное.

Простейший К. п.-в о р о б а. Основная часть ее-колесо или шестиугольник с поставленной вертикально осью; внутри колеса движутся обычно две лошади по направлению, перпендикулярному к его диаметру; наруленая поверхность обода колеса слулеит шкивом для каната, приводящего в действие машину. Недостатком воробы является быстрое утомление лошадей, вызываемое необходимостью делать очень крутые повороты, а таклее значительное трение в цапфах колеса и в направляющих блоках; достоинством же воробы молшо считать ее дешевизну,

в более сложных К. п. имеется передаточный механизм, состоящий из ряда зубчатых колес (фиг. 1). Для более значительного увеличения числа оборотов к К. п. присоединяют ременную передачу или добавочный передаточный станок. Зубчатые колеса применяют в раз.тнчных комбинациях как на

Фиг. 1.

главной раме привода, так и на раме передаточного станка. В конструкцию К. п. должна быть включена пара конических зубчатых колес для передачи вращения от вертикальной оси, вокруг к-рой вращается водило конного привода, к горизонтальной оси приемника молотильных барабанов, ножей соломорезок и т.д. К. п. различают по следующим признакам.

I. в состав механизма входят только зубчатые колеса.

1. Горизонтальные приводы без передаточного станка.

A. Две пары зубчатых колес.

а) Первая пара колес цилиндрическая, вторая коническая:

а) цилиндрические колеса с внешним зацеплением (фиг. 2, А),

/?) цилиндрические колеса с внутренним зацеплением (фиг. 2, Б).

б) Первая пара колес коническая, вторая цилиндрическая (фиг. 2, В).

Б. Приводы с паразитными зубчатыми колесами (фиг. 2, Г).

B. Приводы с планетарной передачей (фиг. 2,Д). Г. Приводы с тремя и более парами зубчатых

колес.

2. Горизонтальные приводы с передаточным станком.

3. Потолочные приводы (фиг. 3 и 4).

II. В состав механизма входят зубчатые колеса и ременная передача.

1. Горизонтальные приводы.

2. Вертикальные приводы.

При применении конич. зубчатых колес необходимо ставить нажимные ролики, т. к. давление на зубец q (фиг. 2, В) разлагается на две составляющие: силу п, направленную перпендикулярно оси и оказывающую такое же действие, как и в случае цйлиндрич. зубчатых колес, и силу t, направленную параллельно оси и стремящуюся изогнуть последнюю действием момента tr, где г-радиус конического зубчатого колеса. Зацепление обеспечивается тем, что обод большого конического зубчатого колеса упирается в нажимной рол ик а (фиг. 1), который принимает на себя силу давления t на зубец. Так как избежать применения конических зубчаток в К. п. нельзя, то следует ставить их в таком месте, где передаваемая сила будет наименьшей. В механизме К. п. принята ускоряющая передача, а потому в первой паре колес сила давления на зубец больше, а во второй уменьшается обратно пропорционально окружной скорости колес; из этого видно, что конические зубчатые колеса следует ставить в последней паре зубчаток.

В цйлиндрич. зубчатых колесах внутреннее зацепление .тучше внешнего. В нервом случае дуга зацепления будет бодьше, чем в случае внешнего зацепления; т. о. усилие распределится на большее число зубцов, и каждый зубец будет менее нагружен. Сила трения при внешнем зацеплении будет пропорциональна сумме чисел зубцов пары находящихся в зацеплении зубчатых колес, а при внутреннем зацеплении пропорциональна разности чисел зубцов. Для К. п. разница в силе трения доходит до 50%, а потому этой потерей не следует пренебрегать. Кроме того зубчатое колесо с внутренним расположением зубцов выполняется в виде колокола или тарелки или же снабжается закраиной, вследствие чего зубцы имеют ббльшую прочность, чем при внешнем расположении. К. п. с внутренним заценлени-ем также наиболее безопасен, так как зубцы его закрыты; недостаток его-трудность очистки зубцов при их засорении.

К. п. строятся на 1, 2, 3 и 4 водила и в зависимости от числа запрягаемых в каждое водило лошадей бывают 1-, 2-, 3-, 4-, 6- и 8-конные. Скорость лошади на К. п. (при движении по кругу) меньше, чем по прямому направлению и считается равной 0,8- 0,9 м/ск, или 3 км/ч. Полезная сила тяги,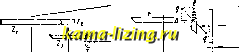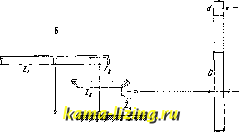

Фиг. 2.

развиваемая лошадью, уменьшается вследствие неудобства движения по кругу, а также вследствие того, что составляющая тяги, направленная вдоль водила, не производит пспезной работы. Практикой выработана обычная длина водила I, равная;