(координационное число). Все остальные атомы (если они имеются) входят в состав внешней сферы и, как более удаленные от центрального атома, связаны с ним слабее; они могут поэтому, в противо-положгюсть атомам внутренней сферы, легко отделяться в виде ионов. Представления Вернера легко м. б. прослежены например на ряде соединений хлорной платины с аммиаком. Присоединяя 2 NHg к PtClj, получаем Р1С14(КНз)2, где число отдельных групп, связанных с центральным атомом Pt, равно в, и следовательно все они могут войти во внутреннюю сферу; соединение это ионов ие образует. При введении двух новых молекул аммиака получается Р1С14-4КНз, где все группы не могут поместиться во внутренней сфере: два атома С1 будут вытеснены во внешнюю сферу, и молекула К. с. примет вид [PtCl24 NHg] Clg (в формулах внутренняя сфера заключается в прямые скобки). Соединение это будет электролитом: оно способно диссоциировать на ионы С1 и на двухвалентный комплексн. катион [PtCl24NH3] . Действительно, в этом случае лишь половина хлора легко и быстро осаждается AgNOg; вторая половина реагирует значительно медленнее. Действуя далее па [PtCl2 4NH3] CI2 аммиаком, получаем соединение [Pt6 NH3] CI4,-соль с комплексн. 4-валентным катионом, во внутренней сфере которой расположены 6 молекул NHg. Аналогичную структуру должен иметь хлоро-платинат калия, [PtCl6]K2; находящиеся во внутренней сфере 6 атомов хлора сообщают комплексу [PtClel характер электроотрицательного кислотного остатка, связываю-ui;ero положительные ионы калия. Измерение молекулярной электропроводности таких солей хорошо подтвернодает изложенную теорию. Координационные ф-лы можно приписывать также гидратам солей, напр.: [СабНаО] CI2; [ZneHgO] (NOs); [AI6H2O] CI3 и т. д. Сульфаты, кристаллизующиеся с 7 молехсулами воды, также могутбыть изобра-лч,ены координационными ф-лами: [ZnGHaO] (SO4H2O); [NieHaO] (804НгО). Замена в них остатка (SO4H2O) на (XSO4) (здесь X-щелочной металл) приводит к известному ряду двойных сернокислых солей типа:

[МебНаО] (XSO4) .

Меледу приведенными выше аммиакатами и гидратами возмолеен непрерывный переход:

[Сг 6NH,1 Gh; [Сг 5NH,HjO] CI,; [Cr 4NH,2H,0] CI,; [Cr 3NH, 3H,0] CI,; [Cr 2NH, 4HaO] CU; [Cr бНгО] СЬ .

Координационная теория позволяет развить совершенно новый взгляд на строение гидратов кислот и солей: их можно рассматривать также как соединения оксония, т. о. кислорода, имеющего координационное чисто 3:

[S)o-

С1 или

Для объяснения многочисленных случаев изомерии К. с. Вернер приписывает атомам, находящимся во внутренней сфере, определенное пространственное располо-леение. В соединениях с координационным числом, равным 4, атомы или молекулы располагаются по углам квадрата; например

соединение [Pt4NH3]Cl2 имеет следующее строение:

NH3 NH,

NH J

CI,.

При замещении двух молекул NH3 двумя атомами С1 возмолшы два изомера:

соль Пейроне соль 2-го основания Рейзе

С1.

NH,-

NHaJ

NHa

CI NH,J trans - форма

cis - форма

Оба изомера действительно известны; третий изомер, имеющий тот лее состав, но вдвое больший молекул, вес-зеленая соль Магнуса, [Pt4NH3][Pt4Cl], является комплексной солью комплексной кы. В соединениях с координационным числом, равным 6, группы внутренней сферы распололеены в вершинах правильного октаэдра; таков например катион соединения [C06NH3] CI3. При замещении 2молекулNH3 двумя rpynnaMnNOa здесь также возмолепы и найдены два изомера: cis-форма (флавосоль, фиг. 1) и trans-форма (кроцеосоль, фиг. 2); они различаются между собою по растворимости, цвету и химич. свойствам. Октаэдрическ. модель позволяет также предвидеть возможность оптич.

[А с с Me g JJ .

Вернеру удалось получить изомерные оптически деятельные соединения кобальта, хрома, леелеза и ряда др. элементов, что явилось блестящим подтвернедением развитой им нее теории. В последнее время Шерер и Столле при помощи рентгеновского анализа определили истинное расположение атомов в кристаллах хлороплатината калия KgPtCle, или [PtCl6]K2. Оказалось, что в элементарн.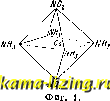

ячейке криста.тлич. решетки канедый атом Pt окружен Шестью атомами CI, расположенными в вершинах октаэдра, а атомы К находятся на большем расстоянии и располагаются в вершинах кубов, центрами к-рых являются атомгэ[ Pt; таким образом теория Вернера получила новое веское подтверждение. В настоящее время исследование К. с. направлено к выяснению природы и характера сил, связывающих отдельные части комплексных молекул.

Лит.: Ч у г а с и Л. А., Теория строения комплексных соедннеиии, М., 1910; Ч и ч и б а б и ir А., Координационная теория Вернера-см. Менделеев Д. П., Основы химии, т. 2. М.-Л., 1929; Ч у г а е в, Новые идеи в химии , СПБ, 191-i, 1; Werner А., Neu те Anschaungen auf d. Oebiete d. anorgnnisclien Cheniie, 5 Auf!., bearb. v. P. Pffiffer, Braunprhweig, li:t23; E p h r a i m Fr., Anorganische Chemie Dresden - Lpz., 1923. A. Моносзон.

КОМПЛЕКСНЫЕ ЧИСЛА, числа вида а + Ы, где а и b-действительные числа (положительные И.т1и отрицательные и в частности м. б. нулями), %--м н и м а я единица, удовлетворяющая ур-ию: = -1, что

обычно выражается так: i = l . Очевидно

= -г, г* = 1, г = г,... Действительные числа являются частным случаем К.ч., когда b = О; если же а==0 и ЪфО, то получаем чисто мнимое число Ы; К. ч. есть нуль, если а=Ь = 0; а называется действительной частью К. ч.; Ы-мнимой частью, Ъ - коэфициентом при мнимой части. Два К. ч. равны, если равны действительные части и коэфициенты при мнимых. Два К. ч., отличаюптиеся лишь знаком при мнимой части, а + Ыя а - Ы, называются сопряженными. Часто К. ч. изображается одной буквой: а -Ь Ы= z.

Геометрическая интерпретация К.ч. Берем систему прямоугольных декартовых координат на плоскости; называем ось абсцисс де11ствит. осью, ось ординат- мнимою; изображаем К. ч., а-\-Ы, точкой М с координатами (а,Ь) или вектором ОМ. Если введем на плоскости полярные координаты a = rcos(p, b = rsmfp, то К. ч. примет вид:а-Ь Ы=г {cosfp-{-гвшср) (тригонометрич. форма К. ч.); г= -Ь /а -1- называется модулем К. ч.; он выражает длину вектора ОМ и изображается символом \а-\-Ы\; угол tp называется аргументом К.ч. Положительные действительные числа имеют аргумент О, отрицательные п; аргумент определяется не однозначно, а с точностью до слагаемого 2kn (где к-любое целое число), т. к. от прибавления целого чиста окружностей значения cos 9? и sin 95 не изменяются. Сопряженные К. ч. имеют равные модули и противопололшые аргументы.

Сложение двух К. ч. а + М и а + Ьг совершается по правилу:

(а -Ь Ы) + (а -Ь Ьг) = {a + a) + i{b + Ъ). Геометрически сумма представится диагональю параллелограмма, построенного на векторах, изображающих слагаемые (фиг. 1).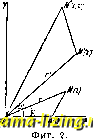

Фиг. 1.

Слолсение векторов на плоскости-см. Векторное исчисление. Сумма сопряженных чисел равна (а + Ы) + (а - Ы) == 2а,-действительному числу. Из геометрическ. интерпретации (сторона треугольника меньше суммы двух других сторон) следует: модуль суммы сумме модулей.

Вычитание К. ч. дается ф-лой:

(а + Ы) - (а -Ь Ьъ) = ( - )+*(&- &) Умножение К. ч. производят по правилу умножения многочленов, принимая во внимание условие = - 1. Таким образом г z=(a + bi) {a -{-bi) = aa - bb+i (ab+ab). Если перейти к тригонометрической форме, Z = г (cos (р + г sin q>), z = r {coscp + i sin97), TO формула умножения даст:

z z = rr [cos {(p rf- 95) -(- г sin {(p -}- 9?)], T. e. при умножении К. ч. модули перемножаются, а аргументы складываются. Геометрич. построение точки Ж , изображающей произведение zz: на действительной оси (фиг. 2) берем точку А, изображающую 1, и на отрезке ОМстроим Д ОММ ,подобный Д ОАМ. Т. о. геометрич. смысл умножения Z яа z таков: изменяем длину вектора множимого в отношении г (модуль множителя) и поворачиваем этот вектор на угол (р (аргумент множителя). Произведение двух сопряженных К. ч, равно действительному числу, квадрату модуля: (а -f bi)-(a-bi) = -f = а + Ъг\ = а - Ы\\ При делении К.ч. частное выражают в виде дроби и умножают числитель и знаменатель на число, сопряженное знаменателю, чтобы избавиться от мнимости в знаменателе:

2 а + Ы (а + Ы)(а- bi) z ~ а + bi~ (а + bi)(а - Ьг)

аа + bb ab - ab

Деление невозмолшо лишь в случае, когда а= & = О (деление на нуль). В тригонометрической форме имеем:

7 = [cos (9? -(p) + i sin (q> - q>)].

Возведение в степень. Пользуясь тригонометрич. формой К. ч.

.2; = r(cos9 -f-г sin 9?) и применяя ф-лу умножения п раз, получим:

0 = r*(cos П(р sin п(р), т.е. модуль возводится в степень, а аргумент умножается па показатель. Полагая в частности г=1, имеем тождество:

(cos 9? -f г sin 9?) = cos nq) + г sin nq) (ф-л a M о a в p a). Приравнивая в обеих частях действительную и мнимую части, имеем тригонометрич. тождества:

cos nq> = COS (р - COS ~2g5 sin2 (p

-f cos *9? sinV -

sin П9? = j cos ?? sin 9? - Qjcos 2 9?sin9J-b

-f- cos*~5 9? sin 9? - ...

При извлечении корня n-йстепени надо извлечь корень из модуля и разделить аргумент; в виду неоднозначности аргумента получается п различных значений корня. Пусть

0 = г (cos 9? 4-г sin 97),

где О 93 < 2я; очевидно, что таклсе

z = r [cos {q) + 2п) + i sin (93 -Ь 2л), ... ;

тогда уг дает всего п разных значений:

f/-(cos-f tsin);

rr(cos-Visin);

[cos ±l(-zA)L + i sin 1±1 Щ

Если в частности

л = 1 = cos2/£л 4-г sin 2?сл! (?с = 0,+1,...), то

Vl = cos- + isin~ = l;

п- 2л , . . 2л: .

]/1 = COS--\- I Sin - ,

!у7 2{п - 1)л , . . 2(п

у1 = COS------- -f г sin - - .

Все ЭТИ корни расположатся в вершинах правильного и-угольника, вписанного в круг радиуса 1.

Показательная форма К.ч. Определим значение показательной функции для мнимого показателя помощью ряда Тейлора (см. Дифференциальное исчисление):

4- 1 М г

I 911 Г ql Г

= 1-2 +4!-...+4l 3! + ...)-

Действительная часть и коэфициент при г в правой части представляют собой разлолее-ния cos9f и sin??. Таким образом

6= cos 9?-Ь г sin 9 ; (1)

заменяя г на -г, получим:

е~= cos?? -isin . (2)

Из формул (1) и (2) получаем выражения тригонометрических ф-ий через мнимые показательные:

cos (р =

sin 9? =

(ф-лы Эйлера). Подставляя выралеение (1) в К. ч. (в тригонометрич. форме), получаем показательную форму:

Z = ге (г-модуль, 95-аргумент).

Заметим, что из ф-лы (1), в к-рой принимаем (р = 2кл, на основании толодества: cos 2кл + i sin 2Ы = 1,

пол\Т1им:

6*= 1 (7с = О, ±1, ±2,...).

Были сделаны многочисленные попытки (Гросман, Гамильтон)ностроить более сложные комплексные числа т. о., чтобы действия над ними сохраняли законы обычных арифметических операций. Это однако оказалось невозможным. Различные системы так. наз. гиперкомплексных чисел построены, но действия над ними всегда в том или ином отношении отличаются от действий над обыкновенными числами. Наибольшее значение имеют т. наз. кватернионы Гамильтона, приведшие к современной теории векторов (см. Векторное исчисление). Кватернионы-гиперкомплексные числа с 4 независимыми единицами: 1, г, j, к. Общи11 вид кватерниона:

q = d -\-га jb + кс

{d, а, Ь, с-действительные числа); в этом выражении d называется скалярной частью и га + jb + кс есть вектор в пространстве. При сложении кватернионов Складываются скалярные части и компоненты вектора; умножение распределитель-

но и сочетательно и определяется законом умножения единиц:

ij = к. jk = i; ki = /; г- = у- = = -1; ji = - ij ; kj = - jk; гк = - ki (умножение не перемест и тельн о). По этому правилу произведение двух векторов дает кватернион, у которого скалярная часть есть внутреннее (скалярное) произведение векторов с обратным знаком, а вектор-внешнее (векторное) произведение векторов:

(ia -Ь jb -}- кс) (ix jy + kz) - ах - by - с.г-Ь + i{bz - су) -f j {сх - az) + fc {ay - bx).

В тригонометрич. форме кватернион выражается следующим образом:

q = r cos D -f гг sin D cos a -(- jr sin D cos fi -\~ -f fcr sin D cos 7= r (cosD + e sinD),

здесь e-единичный вектор в направлении оси кватерниона, которая образует углы а, /3, у с тремя взаимно перпендикулярными векторами г, j, к; D называется углом кватерниона, г = Vd- а + Ь -\- с его тензором (нормой). При D = ~ по.лучается чистый вектор. Кватернионы имеют прилолсение в механике (твердого тела) вследствие их геометрическ. значения: с их помощью изображается поворот в пространстве около оси кватерниона на уго.л D, с одновременным растялеением (снеатием) в отношении г.

Лит.: Л а X т и н Л. К.. Энциклопедия элементарной математики, ч. 1, М., 1924; Привалов И. И., Введение в теорию функций комплексного переменного, М.-Л., 1927; Н а m 111 о п W. R., Elements of Quaternions, V. 1-2, L., 1899-1901; Backer, Quaternions, London, 1911. B. Степанов.

КОМПРЕССОРЫ, машины для сжатия воздуха и других газов и паров до б. или м. высокого давления. Строгой границы между К. и воздуходувными машинами (см.) провести нельзя; можно сказать, что К. называется воздуходувная машина, слдамающая воздух от4-5 aim и выше. К. делятся на два больщих класса: поршневые компрессоры и турбокомпрессоры. Основным процессом в тех и других является сжатие газа.

Сжатие в К. В основных расчетах К. сжатие принимают происходящим или без сообщения и отнятия тепла (адиабатически), или при сохранении постоянной р\ t° (изотермически), и.ли наконец по какой-либо нро-межуточ.кривой (и о-л и т р о п а). Так как степень сжатия в одном цилиндре К. не бывает никогда особенно большой, то моншо делать расчеты для воздуха и других газов, принимая теплоемкости постоянными и вообще пользуясь законом для идеа.льных газов. Рассматривая идеальные процессы для К. (фиг. 1), не принимая во внимание величины вредного пространства, понижения дав.ления при всасывании вследствие имеющих место сопротив-

Фиг. 1.