некоторые затруднения. Если же ядро уравнения (2) непрерывно и дифференцируемо, то, дифференцируя ур-ие (2) по ж, получаем:

fix) = К(х, х)<р{х) + f Ка: (х, S) <р(8) ds ;

предполагая К{х, х)ФО, можем разделить обе части ур-ия на него; применяя новые обозначения, получим ур-ие вида:

fix) = 9? (ж) -Ь jf Kix, s) <p(.s) ds ,

уравнение Вольтерра 2-го рода (к и /-известны, (р-ищется). Для решения уравнения (3) вводим параметр А и составляем уравнение вида:

<pis) = Я / liC (ж, s) ф) ds + fix) . (30 о

Ипдем решение в виде степенного ряда: (pix) = (poix) + A/Pi (ж) + (ж) +

+ ...+;.>, (ж)+ .- (4)

Подставляя выражение (4) в ур-ие (3) и приравнивая коэффициенты при различных степенях Я, находим:

Ч>о(ж) = fix); (Piix) = jKix, s) <Po(s) ds ;

<Piix) jKix, s) (Pxis) ds,...,

4>n(x) = / К ix, s) <p .x is) ds .

Ряд (4) СХОДИТСЯ при всех значениях Я; при Я=1 имеем решение ур-ия (3), Решение (4) можно представить одной формулой. Назовем

/ИГ(ж, t)KH,y) dt = Kix,y), у

/ (ж, 1)КЦ, у) dt = ir<> (ж, 2/),..., у

JК-\х, t)Kit,y)dt=К ix,у),... у

последовательньпли повторениями ядра if. Составим ф-ию:

Г ix, у; Я) = iiC (ж, у) + ж ix, у) -f

+ ... +к-к\х,у)+..., (5) т.н. резольвенту ур-ия (3). Тогда решение (4) запишется так:

ipix) = fix) + Jrix, s; X)fis)ds.

Наряду с и. у. Вольтерра в прилолсениях встречаются и и те г р о-дифференци-а л ь н ы е ур-ия, где вместе с искомой ф-ией (р входят также ее производные (как под знаком интеграла, так и вне его). Обыкновенно рассматриваются интегро-дифференциаль-ные ур-ия линейные (в к-рых искомая ф-ия и ее производные входят линейно).

Другой важный тип И. у.-у равнение Фредгольма. Общий вид ур-ия Фред-гольма (2-го рода):

<pix) ==fK ix, s) <pis) ds + fix).

Здесь опять К (ядро) и /-данные ф-ии, дз-

искомая ф-ия; отлише от ур-ия Вольтерра в том, что оба предела интеграции а я Ь постоянны. Мы попрежнему рассматриваем более общее уравнение

<Pix) XjKix,s) q>is) ds + fix). (6)

И здесь можно искать разложение в форме (4), при чем будем иметь:

nix) = fix); <Pxix) = jKix, s) (Pois) ds,

(Piix) = J Kix, s) <Pi(s) ds,...,

4>n(.x) = / IT (ж, s) (Pn-i is) ds.

Повторения ядра для И. у. Фредгольма определятся так:

fKix,s)Kis,y)dy = K<Hx,y),

JЮ> ix, s) Kis, у) dy = Юх, у),....

JK- ix, s)Kis, у) dy = Kix, y)

С ЭТИМИ новыми выражениями повторений резольвента Г ix, у; Я) выразится той же ф-лой (5), а решения ур-ия (6)-

<pix) = fix) + xfrix,s; Я) fis) ds . (7)

Но в и. у. фредгольма встречается особенность: ряд (5) сходится только для значений Я, достаточно малых по модулю. Фредголь-му удалось дать выражение резольвенты для всех значений Я в виде частного двух ф-ий, целых относительно Я:

Пх,у; A) = -v-

Для значений Я, не обращающих в нуль знаменатель, решение ур-ия (6) дается ф-лой (7); если же 1)(Я)=0 для Я=с, то уравнение (6) при произвольной ф-ии fix) вообще не имеет решения; зато имеет решение (одно или несколько), отличное от нуля, соответствующее однородное ур-ие: ъ

<Pix) = ejKix, s) (р is) ds . (8)

Эти значения с называются фундаментальными числами, а соответствующие им решения ур-ия (8)-ф у н д а м е н-, тальными функциями. Особенно интересный класс представляют И. у. с симметричным ядром, т. е. такие, где Kix, y)=Kiy, ж). Здесь мы имеем следующие свойства: всякое симметричное ядро обладает хоть одним фундаментальным числом (собственным значением); все соб- \ ственные значения Ях, Яа, ... действительны; соответствующие им фундаментальные (соб- . ственные) ф-ии <Piix), (рix)можно выбрать I так, что они образуют ортогональную систему в интервале (а,Ь), т. е.. ;

6 .I

/ fPiix) q>j,ix)dx = Q iгфk); \

такова, напрйм., система 1, cos аз, cos2ic ., since, sin 2ж,... в интервале (0; 2л).

Так как собственные функции определяются с точностью до постоянного множителя, то их можно предполагать нормирован ными, т. е.

Jl<Pi(.x)fdx=l.

Если симметричное ядро имеет только конечное число собственных значений, а собственные функции приведены к ортогональной и нормальной системе, то имеет место равенство:

(нек-рые м. б. равны между собою). Равенство (9) имеет место и для случая бесконечного множества чисел при некоторых ограничениях, наложенных на ядро. При этих условиях резольвента имеет вид:

Связь и. у. с дифференциальными уравнениями. Многие задачи математической физики (напр. колебание неоднородной струны с закрепленными концами) приводятся к решению дифференциального ур-ия 2-го порядка:

(риУ -ди + Ы = 0, (10)

с граничными условиями: и(а) = 0, м(Ь)=0; (р, q-ф-ии от X, р>0; Л-неизвестная постоянная)! Ур-ие (10) приводится к И, у. типа Фредгольма с симметричным ядром. Для этого строим функцию Грина G{x,$). Это есть решение дифференциального ур-ия (риУ- qu=0, удовлетворяющее граничным условиям, непрерывное между а и 6; но 1-я производная по х имеет в точке (а < < Ь) разрьш непрерывности:

IdGjx, 1)1 i

L Эх J p(i)

Функция Грина удовлетворяет условию симметрии: G(x, ) = G(, х), и всякое решение ур-ия (10) удовлетворяет однородному И. у. (2-го рода):

u(x)=?.jG(x,i)u{i)d$.

На основании изложенной теории, это Й. у. имеет отличные от нуля решения лишь тогда, когда Я равно одному из собственных значений А,-; соответственные решения и(х) = (Pi(x) будут собственные ф-ии; они образуют ортогональную систему. Решение неоднородного дифференциального ур-ия (риУ - ди + Ы = у!{х)

сводится к интегральному уравнению неоднородному:

и{х) = А / Gix, I) uQ) + gix) ,

где g(x) = - j* G(x, ) v (Г) d. Теория И. у.

легко обобщается на случай, когда искомая

функция зависит от нескольких аргументов, например, на уравнения Фредгольма: ь ь

4>{х, У) = S S К{х, у, s V) <Р{, V) dr] -f /(ж, у).

Эти ур-ия могут служить ДЛЯ решения проблемы Дирихле и Неймана (см. Потенциал) или, напр., задачи о плотности электричества на проводнике данной формы (задача Робена) и т. д.

Лит.: Беленовский П. Д.. Интегральные уравнения и их роль в математическ. физике, Вятка, 1928: Courant R. и. Hilbert D., Methoden d.mathemat. Physik, В. 1, В., 1924; Kneser А., Integralgleichungen u. ihre Anwendung auf die ma-themat. Physik, 2 Aufl.. Brschw., 1922; G о u г s a t E., Cours dAnalyse, 3 6d., t. 3, P., 1922. B. Степанов.

ИНТЕГРАТОРЫ, см. Интегрирующие приборы.

ИНТЕГРИРУЮЩИЕ ПРИБОРЫ, приборы, осуществляющие чисто механич. путем интегрирование нек-рой заданной обычно графически ф-ии. Двум задачам интегра-пьного исчисления-нахождению определенного интеграла и нахождению интегральной кривой-соответствуют две группы интегрирующих приборов. К первой группе относятся: 1) планиметры, т. е. приборы, служащие для нахождения площади, ограниченной заданным контуром; 2) интеграторы, дающие значения определенных инте-b ь b

гралов J /(ж) dx, J f\x) dx, J fix) dx для ф-ии a a a

fix), заданной графически, и 3) гармонические анализаторы (см. Гарлшниче-ский анализ). Ко второй группе относятся интеграфы, т. е. приборы, вычерчивающие по заданному ур-ию fix,y,,..., ) = О интегральную кривую y-(pix) и, в простейшем случае, по уравнению = (ж) - кривую 2/ = J Fix) dx.

В основе конструкции большинства наиболее употребительных планиметров и интеграторов лежат следующие соображения. Пусть отрезок прямой ВА скользит по плоскости; при своем движении он зачерчивает

Л. А. А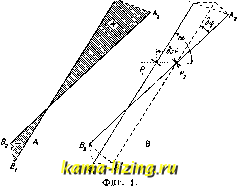

нек-рую площадь; условимся считать ее положительной, если для наблюдателя, смотрящего по направлению стрелки, она остается влево, и отрицательной, если она остается вправо от движущегося отрезка. Тогда вся площадь, зачерченная отрезком при

перемещении его из положения AiB в АВ, выразится в виде суммы положительных и отрицательных площадей (фиг. 1, А). Как известно, элементарное перемещение в плоскости м. б, разложено на поступательное перемещение, определяемое перемещением произвольно выбранной точки Р, и на вращение вокруг этой точки. Вообразим на нашем отрезке (фиг. 1, В) в точке Pi колесико, имеющее своей осью отрезок ВА и при его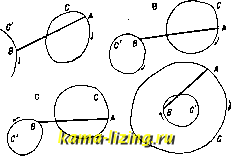

Фиг. 2.

движении катящееся по плоскости. Из двух указанных выше элементарных движений только поступательное движение вызовет

с й8 sin а

вращение колесика на угол осо = ---, где

Ss-перемещение точки Pi, а-угол между этим перемещением и направлением отрезка и г-радиус колесика. Элементарная же площадь, зачерченная при этом перемещении,

будетравнаМ58ша-Ь(ф)9ь-()й<,;

здесь I-длина отрезка, - = вф и дд>-эле-ментарный угол поворота отрезка. Последнее выражение можно представить в виде

1т8т + Цд<р, где 1 = 1 от середины отрезка. Обведем концом Ах

-расстояние Pi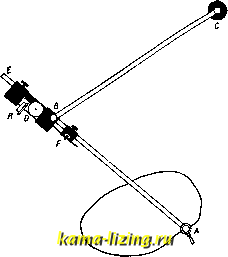

Фиг. 3.

отрезка контур, ограничивающий площадь, подлежащую определению, т.о.,чтобы после этого отрезок ВхАх вернулся в свое исходное

положение. Зачерченная площадь будет тогда равна Y,lr 8cd 8(р = Irto -j- Цч>, где

со-угол поворота колесика вокруг его оси, а (р-угол поворота отрезка. Так как отрезок возвращается в свое исходное положение, то угол 9:=0 (фиг. 2, А, В, С) или (р =2л (фиг. 2, D); Обозначая через (С) и (С) площади, ограниченные контурами Си С,получим для четырех случаев, изображенных на фиг. 2, соответственно:

(С) = гг(ы; (СО - (С) = ггсо; (С) -Ь (С) = Iroj; (С) - (СО = 1гш -f гпЦ .

Полярный планиметр Амслера (фиг. 3) есть непосредственное применение изложенной теории. В нем точка В ведется с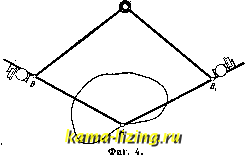

по окружности круга с центром в С, и, в зависимости от размеров обмериваемой площади и расположения прибора, мы имеем или случай А или случай D (фиг. 2). Целое число оборотов колесика R отсчиты-вается на циферблате D, доли же оборота- на барабане, укрепленном на колесике. Длина 1=ВА может изменяться передвижением стержня АЕ. Для малых передвижений служит микрометрический винт F. На плани метре, представленном на фиг. 3, ось колесика не совпадает с линией АВ, но нетрудно видеть, что при параллельности линии АВ отсчет по колесику от этого не изменится, если за точку Р считать пересечение АВ с плоскостью колесика. При непараллельности появляется систематическая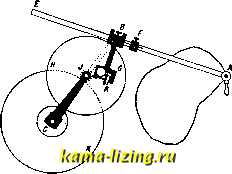

Фиг. 5.

ошибка прибора, для исключения которой рекомендуется обвести контур дважды при двух различных положениях прибора(фиг.4) и брать полусумму отсчетов. Описанная конструкция представляет два неудобства: