Фиг. 2.

рассмотренного вида. Иногда выгодно применить полярные координаты. Пусть ур-ие кривой r = f{(p). Площадь сектора (фиг. 2) АОВ разбиваем на п элементарных секторов с углами при вершине Aq>i. Каждый такой сектор представим по избытку и недостатку как

круговой, по ф-лам ~ Дд? и Aq>, где

Mf и m-наибольший и наименьший радиусы-векторы. В пределе при w- ooполучим:

площадь АОВ = lfr(p = lJ [fi<p)] dq>.

Если замкнутая кривая окружает начало, за пределы интеграции принимают О я 2л.

П-р и мер. Ур-ие круга в полярных координатах г=а. Площадь круга равна

Длина дуги. Дифференциал дуги (см. Дифференциальная геометрия) ds = = Vdx + dy. Если кривая задана ур-ием у = = /(ж), то ее дуга между точками с абсциссами а и Ь равна

JVl + [nx)f dx.

В случае параметрич. ур-ий

Пример. Для циклоиды дифференциал дуга

ds = 2а sin dt. Длина одной ветви

t V t~\

s = 2а J sin 2 = - 4а icoSg =8a.

Длина дуги в полярных координатах дается формулой:

s = JVdr~+r4.

Объем тела вращения. Кривая y=f{x) вращается около оси абсцисс; требуется определить объем, ограниченный поверхностью вращения и плоскостями ж=а, х=Ь. Разбивая объем на элементарные, которые вьршсляем по избытку и недостатку как круглые цилиндры, и переходя к пределу, найдем:

F = я/2/2 ж = я / [/(ж)]2 йж .

а а

Вообще, если у тела любой формы площади сечений, перпендикулярных к оси абсцисс, известны в ф-ии ж, напр. X, то объем выразится следующим образом:

VJXdx.

Ц,римвр. Найти объем эллипсоида При данном Ж имеем в сечении эллипс

Ь (а - зс ) а

с (а* - х) а

С полуосями Уа - ж* и Уа - з и с площадью (а*-ж). Искомый объем

. Ла .

Г = /(а -ж2)йж = яа&с.

Поверхность тела вращения S выражается интегралом:

ft 6

S2Jyds = 2Mj fix) У1 + [fix)f dx .

Центр тяжести. В механике координаты ц. т. системы точек Pj с массой т и координатами (Жх, yi),Pzim2,X2,y2)--- даются формулами:

£ mjXi s miVi

Если масса распределена непрерьшно, мы совершаем переход к пределу и вместо сумм получаем интегралы.

1) Центр тялгести дуги. Принимая массу единицы длины равной 1, будем иметь:

Sxds

Svds а

J-ds

2)Центртягкести плоской фигуры. Считаем массу единицы площади равной 1. Берем криволинейную трапецию, разбиваем ее на полоски и заменяем их прямоугольниками. Замечая, что площадь элементарного прямоугольника равна ух, а ц. т. находится на половине высоты, получаем, переходя к пределу:

Sxy dx а

Svdx

1 ь а Ь

fy dx

Пример. Найти ц. т. полукруга у = + Уа-х.

Очевидно

5 = 0; 2/ = / (а-ж2)йж:ла = .

Момент инерции плоской фигуры. Момент инерции относительно оси абсцисс конечной системы точек 1д. имеет выражение: Ij; = 2 mj- у% а относительно оси ординат: 1у = 2 т.1 ж?. Для криволинейной трапеции &

получим: J хУ dx. Для вычисления 1у

заметим, что момент инерции элементарного прямоугольника равен Дж, откуда

h = kSydx.

Интеграл как функция параметра. Пусть подинтегральная ф-ия зависит, кроме X, еще от параметра t. Интеграл

J f(x, f)dx не зависит, как мы видели, от х, а

НО является ф-ией параметра t. Применяя определение производной, получаем ф-лу:

t)dx = Jlj{x, t)dx,

дающую правило дифференцирования определенного интеграла по параметру. Если -пределы интегрирования а и & тоже зависят от *, формула примет вид:

1-/f(x,t)dx = f§-Kx,t)dx +

Определенный интеграл как ф-ию параметра можно также интегрировать по параметру. В случае постоянных пределов имеем:

/ { }пх, t)dx }dt = S{ Snx, t)dt } dx,

a a a a

Т.е. порядок интегрирования по переменному и по параметру можно менять. В случае бесконечных пределов интеграции это правило справедливо только в случае равномерной сходимости интеграла J* f(x, t) dx; это

значит: для сколь угодно малого е можно найти достаточно большое Ь так, что

fix, t) dx

для всех значений t в пределах интеграции.

Приближенное вычисление интегралов (механические квадратур ы)-см. Вы-чжления приближенные.

Интегрирование рядов-см. Ряды.

Двойные интегралы. Дана непрерывная ф-ия от двух переменных / (ж, у). Уравнение z = fix, у) геометрически представит поверхность. Требуется определить объем,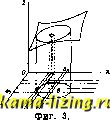

Фиг. 4.

ограниченный этой поверхностью, плоскостью XY и цилиндрич. поверхностью, направляющая которой-замкнутая кривая С на плоскости XY. Разбиваем плоскость XY прямыми, параллельными осям координат, на маленькие прямоугольные площадки Ах-Ау и через линии деления проводим плоскости, параллельные 0Z (фиг. 3). Отберем те прямоугольники, к-рые имеют обпще точки с площадью В, ограниченной кривою С;

в каждом прямоугольнике берем соответствующее значение f{x,y), напр. fiXi,y), и составляем сумму: S /(ж, if) Дж Ау . Предел этой суммы, когда Дж и Ау стремятся к нулю, запишется как JJ /(ж, y)dxdy (двойной ин-

теграл, распространенный на область В). Геометрически он представит искомый объем. Для вычисления двойного интеграла производим под знаком S суммирование сначала по у, потом по ж (или наоборот). Предположим, что кривая пересекается параллелями к оси ординат в двух точках. При переходе к пределу придется сначала интегрировать по у от М до N, затем по ж от а до b (фиг. 4). Для аналитическ. выражения предположим, что дуга АМВ дана ур-ием y=<Pi{x), дуга AN В-ур-ием y=Pi{x). Тогда

Ь (Pi(x)

S S /(ж. У) dy= S dxj fix, у) dy .

(В) а 4>i(x)

В частности, если В-прямоугольник, ограниченней прямыми: х~а; х=Ь; у=с; y=d, получим:

. ь d J / /(ж, 2/) dxdy dxjf (ж, у) dy

(Б) .а с

(пределы по у также постоянны).

Замена переменных в двойном интеграле. Пусть надо ввести такие переменные и и V, что x=(piu, v), y==y>iu,v). Тогда имеем ф-лу:

SS f у) У= / f9 ) V(w, V)] 1Di dudv,

(В) iW)

где D есть определитель Якоб и:

ди dv 9v ду> ди dv

а W-область плоскости iu,v), в которую переходит область В. В частности, при переходе к полярным координатам х~г cos у, =г sin gj, имеем:

дх дх дг д<р ду ду дг д9

следовательно,

Sjifix, у) dxdy = JJ fir cos , г ain q>)r dr dq>. Пример. Интеграл Пуассона

IJe-dx.

Имеем

= j e-=* dx f e-v dy = j e-*-v* dx dy

двойной интеграл, распространенный на всю площадь. Переходим к полярным координатам:

2л 09

! = JJe-dr d(p J d<p J e-rdr=Tc,

следовательно, 1 = 1

Приложениядвойного интеграла. Кроме вычисления объемов, двойной интеграл служит для вычисления кривых

поверхностей. Здесь имеем ф-лу: площадь поверхности z = f(x, у), ограниченной цилиндром с направляющей С:

S = JSVl + n-hndxdy,

дх 1 ду

Координаты ц. т. площади .В выразятся так: SSxdxdy

Sfydx dy - (В)

В и- в

Момент инерции площади В относительно оси ординат:

I = JJx dx dy.

Тройной интеграл. Дается функция трех переменных /(ж, у, z) и область В, ограниченная поверхностью S. Пространство разбивается плоскостями, параллельными координатным, на малые параллелепипеды и составляется сумма произведений значений ф-ии внутри параллелепипеда на его объем:

f(.Xi,yk,zi) Ах Ау Az;

знак суммы распространяется на параллелепипеды, имеющие общие точки с В. Предел этой суммы есть тройной интеграл: j/( У ) dx dy dz. Его вычисление сво-(В)

дится к последовательному интегрированию сначала по х, затем по у, наконец - по z. Тройной интеграл применяется к вычислению ц. т. и моментов инерции объемов, также в гидромеханике, теории потенциала и т.д.

Криволинейные интег-ралы. Пусть дана функция fix, у) и на плоскости XY кривая С: х=<рЦ), 2/ = v(0- Под криволинейным интегралом по кривой С от точки АЦ) до точки В(*х). т. е. /Р(ж, у) dx, понимается

интеграл J P[q>ii)wi014>it)dt. Этот интеграл

зависит от направления кривой: интеграл от В до J. равен интегралу от А до В, взятому с обратным знаком. Аналогично определяется jQix,y)dy и наиболее общий криволинейный интеграл

JPdx+Qdy.

Если, в частности, кривая С замкнутая и ограничивает область В, то существует следующая связь криволинейного интеграла с двойным (ф-ла ГрИна):

(С) (В)

Подобно криволинейному интегралу определяется интеграл по поверхности. Имеем ф-ию от 3 переменных Е(ж, y,z) и поверхность S; тогда

JJB (ж, y,z)dxdy = JJR (ж, у, z) cosy da , (S)

где x,y, z выражены в функции переменных и, V (см. Дифференциальная геометрия), da-элемент площади поверхности, у-угол

нормали с осью 0Z, Наиболее общий интеграл по поверхности

JJPdy dz + Qdzdx+Rdx dy

= jj (p cosa -- Q cos/5 -t R cosy) da,

где a и -углы нормали с осями OX и OY. Если поверхность S замкнута и ограничивает объем V., то этот интеграл равен

Snii+fyu)y (ф-ла Остро-

градско го-Грина). Пусть в пространстве дан криволинейный интеграл j Р йж -Ь

4- Q dy-\- Rdz. Если кривая L замкнутая, то этот интеграл можно выразить через двойной интеграл по части произвольной поверхности 27, ограниченной кривою L; а именно, имеет место равенство (формула Стокса):

jPdx-\-Qdy+Rdz = -m-mdydz +

Эти формулы имеют большое применение в механике; их более простую запись и геометрическую интерпретацию дает векторное жчисление (см.).

Лит.: г у р с а Э., Курс математич. анализа, пер. с франц., т. 1, М., 1911; Филипс Г., Интегральное исчисление, пер. с англ., М.-Л., 1927; Гренвиль В., Элементы диффер. и интегр. исчисления, пер. с англ., ч. 2, 6 изд., М.-Л., 1928; Б и-б ер б ах Л., Дифференциальное и интегральное исчисление, цер. с нем., ч. 2-Интегральное исчисление, М., 1924. В. Степанов.

ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ, ур-ия, в к-рых искомая ф-ия входит под знаком интеграла. Первое И. у. получено и решено Абелем, исследовавшим механич. задачу: определить вид кривой, по к-рой движется маятник, если время колебания Т есть данная ф-ия наибольшей высоты. Представляя ур-ие искомой кривой в виде 8~Ф iz) is-длина дуги, Z-высота), мы для ф-ии 93 (0) = Ф(0) получаем И. у. Абеля:

где fib,) = / {я-ускорение силы тяжести).Ур-ие (1) имеет решение:

ф(/) = >()й =

Общая теория И. у. создана трудами Воль-терра, Фредгольма, Гильберта и др.

Уравнения Вольтерра 1-го рода являются обобщением ур-ия Абеля; общий вид такого ур-ия:

fix) = fKix,s)<pis)ds,

где / и К-данные ф-ии, (р-искомая ф-ия. Ф-ия К называется ядром И. у.; в случае (1)ядро равно ; оно бесконечно при

Ух - s

x=s; этот случай в общей теории представит