
 |
|
|
Литература --> Изомерия в производственном цикле Фиг. 8. где Су, Су, Су,..., Cj,-коэфф-ты подъемной силы каждого из планов полиплана; С, Csg,..., Сд;-соответственно коэфф-ты лобового сопротивления планов, а >Si, S2, - площади каждого плана. И. с. полиплана, имеющего одинаковой ширины крылья, будет выражаться ф-лой, аналогичной ф-ле (14) моноплана; однако, коэффициент Л будет зависеть не только от относительного размаха плана, но также и от числа планов и их взаимного расположения. Для полипланов приближенное выражение для коэфф. Л будет: где I-наибольший размах полиплана, >S- несущая площадь всех планов, а F-заштрихованная площадь, показанная на фиг. 8. Если взять частный случай, когда все планы имеют одинаковый размах I, одинаковую ширину крыльев Ь, а расстояние между планами равно ширине, то общая площадь S = n -ъ-г, где п-число планов. В этом случае площадь F можно выразить след. обр.: F = (?г - 1)Ь I, и ф-ла (15) получает такой вид: яА + 4(п-1) В частном случае, при п=1, она переходит в ф-лу для моноплана, выведенную выше. Наиболее часто применяемой на практике задачей является переход от крыла с одним относительным размахом к другому. Если мы имеем для данного размаха А поляру Лилиенталя, то можно определить для каждого угла атаки профильное сопротивление, т. е. найти характеристику этого крыла для бесконечного размаха, вычитая из абсцисс кривой Лилиенталя абсциссы параболы И. с, построенной для значения А. Находя параболу И. с. для другого относительного размаха X и прикладьшая к нему профильное сопротивление, найдем новую поляру для относительного размаха Я. Однако, от относительного размаха зависит также и скос потока; поэтому при определенных значениях подъемной силы как при бесконечном размахе, так и при новом конечном Я углы атаки изменятся за счет различных скосов потока. Вычисление характеристики крыла при переходе от одного размаха к другому можно делать графич. или аналитич. путем. На фиг. 9 показан графич. метод такого вычисления при нахождении самой поляры. Остается определить те углы атаки, соответствующие определенному Су,  Фиг. 9. к-рые получатся при переходе ототноситель-ного размаха Я к относительному размаху Я. Угол скоса потока выражается ф-лой: Аа = ЛСу. (16) Если вьгаислить А для значения Я, соответствующего относительному размаху первоначальной характеристики, то можно найти скосы потока, получающиеся при этом крыле. Истинный угол атаки а -Да равен кажущемуся углу атаки для крыла бесконечного размаха. Если мы имеем значения Су, выражаемые кривой по углу атаки а, то, проведя налево от оси ординат прямую (фиг. 10), выражаемую ур-ием. (16), получим, что для каждого Су скос потока будет выражаться соответствующей абсциссой этой прямой. Если отнести кривую Су к вышеупомянутой прямой, то получим кривую Су по истинным углам атаки. Если же отнести эту кривую Су к прямой, выражаемой ур-ием \а=АСу, где А соответствует Я, то получим выражение Су по углам атаки, соответ-ствуюпщм относительному размаху Я, По найденной характеристике Су по а для нового относительного размаха Я можно на поляре Лилиенталя нанести и соответствующие каждому значению Су углы атаки. Вместо только что описанных графических операций можно применить тайже и вычисление. Имея характеристику монопланио-го крыла определенного размаха Я, будем, следовательно, иметь соответствующие друг другу величины а, С, и Сх- Впйсьшаем их в первые три столбца таблицы. Таб.т1ица для вычисления характеристики крыла при переходе от одного размаха к другому. 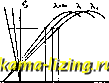 Фиг. 10.
Так как лобовое сопротивление является суммой сопротивлений индуктивного С{ и профильного Ср, при чем Cj- зависит как от относительного размаха Я, так и от соответствующей комбинации крыльев (моноплан, биплан и т. д.), а Ср-от индивидуальных свойств профиля, то переход от одного относительного размаха к другому или от одной комбинации крыльев к другой будет захшю-чаться в соответств:7ющем изменении И. с. Ci, а также и угла атаки а для каждого Су, Т. о., в 4-й столбец вписываются значения Ci для того относительного размаха или для той комбинации крыльев, для к-рой имеется характеристика. Cj-д определяется по ф-ле = С. Вычитая из общего сопротивления Са; И. с. Сд, получим профильное сопротивление Ср С5-Й столбец). Углы атаки. соответствующие определенным Су и Сд-д, будут уже отличны от значений, данных в 1-м столбце, вследствие скоса потока. Этот скос потока, соответствующий бесконечному размаху, определяется по формуле AajACy (6-й столбец). Углы атаки, соответствующие бесконечному размаху данного крыла, найдутся, если вычесть из соответствующего значения 1-го столбца значение 6-го столбца (7-й столбец). Таким образом, 2-й, 5-й и 7-й столбцы дают характеристику крыла бесконечного размаха. Для нахождения характеристики крыла другого относительного размаха Я находим И, с. для относительного размаха Д, к-рое определяется по ф-ле: Сд. = А,- Су (столбец 8-й). Прикладывая к соответствующим значениям Сд, найденное уже профильное сопротивление Ср (5-й столбец), найдем значения лобового сопротивления Су, соответствующие крылу с относительным размахом Я (9-й столбец). Скосы потока для Я определяем по формуле Дод, = J., Су (10-й столбец). В столбец 11-й заносим углы атаки нового крыла с удлинением Я, которые получаются сложением значений столбцов 7-го и 10-го. Т. о., новую характеристику крыла с относительньпл размахом Я будем иметь в столбцах 2-м, 9-м и 11-м. Подобные вычисления проделываются для различных а. Су VL Сд.х в диапазоне имеющейся характеристики (обычно через каждые 2°). Соответствующий анализ показывает, что постоянная по всему размаху скорость скоса, вызванная вихрями, получается в случае распределения циркуляции по размаху по закону полуэллипса. В этом случае И. с. и скос потока выражаются совершенно так же, как и в случае П-образных вихрей, а именно: С, = -С,/ и Да = т. о., средняя вызванная скорость П-образных вихрей одинакова с постоянной скоростью при эллиптическом распределении. Такое распределение циркуляции получается при эллиптической в плане форме крыльев одинакового профиля и одинаковых углов установки. Рассмотренная выше схема П-образных вихрей является схемой искусственной; при рассмотрении сложных крыльев приходится прибегать к более точному методу, ибо эта упрощенная схема дает в таких случаях слишком неточные результаты. Кроме того, если бьшает нужно построить распределение давления по крылу, то приходится уже рассматривать влияние каждого вихря на данную точку исидкости. Ф-ла (5) дает значение вызванной выхрями скорости для любого распределения циркуляции. С другой стороны, в каждом сечении крыла д. б. удовлетворено равенство с.ь = - Зная в каяедом сечении крыла его профиль Су, ширину крыла b и, следовательно, кажущийся угол атаки а, можно найти в каждом сечении скос потока, а также и истинный угол атаки ао = а -Да. Так как в об- щем случае уравнение (5) не интегрируется в простых функциях, то для нахождения характеристики сложного крыла приходится пользоваться следующим приближенным методом. Задаются распределением циркуляции вдоль размаха крыла и определяют в каждом его сечении скос потока Да; зная же Да и угол атаки а, можно найти и а -Да. Затем определяют новую кривую распределения циркуляции по формуле J=CyjbV, rpfi Су-коэфф. подъемной силы профиля данного сечения для бесконечного размаха, соответствующий углу атаки а-Да. Если новая вычисленная кривая не совпадает с той, которою задавались вначале, то следует вновь повторить те же вычисления, задавшись другой кривой распределения циркуляции, промежуточной между вычисленной и ранее заданной. Все эти вычисления чрезвьгаайно кропотливы и требоот много времени; значительное сокращение дает графический метод, описанный в Трудах ЦАГИ , 1929 г., вып. 42. Молено пользоваться таюке и другим аналитическим методом-Трефца, представляющим то удобство, что он сразу дает выражение для распределения циркуляции, при чем устраняется надобность в последовательных приближениях. Сущность этого метода заключается в том, что линия раз-рьша скоростей, являющаяся также границей вихревой области на крыле, преобразуется соответствующими подстановками в круг, а функция потенциала скоростей разлагается в тригонометрич. ряд и д. б. удовлетворена в нескольких точках крьппа по его размаху,-это приводит к решению совместных ур-ий для определения коэффициента этого ряда. Коэфф-ты подъемной силы и И. с. будут, согласно этой теории, выражаться след. образом: (y = Svf 1 (17) Здесь JV = il±Mi±±M±; 3... коэфф-ты тригонометрич. ряда разложения потенциальной ф-ии: 9 = -7-+ -+ -7 + --+... Это ур-ие после соответствующих подстановок и преобразований можно представить в следующем виде: JoSin в = А1$тв(/л + sin в) + + 3sin 39(3/-f sine) + 4- Asin Ъв(Ъ/.1 + sin в) + -bsin79(7 + sin0)-f... (18) Здесь Io = V2 Суо ® половине циркуляции, к-рая получилась бы, если бы каждый элемент рассматриваемого крыла работал так же, как он работал бы при этом же угле установки в плоскопараллельном потоке (т. е. при бесконечном размахе). Су-коэфф. подъемной силы профиля с бесконечным размахом, в-угол между радиусом и осью абсцисс, определяющий положение какого-либо сечения крыла (фиг. 11), /i = iiAli, где 0-гол наклона кривой Су к оси углов атаки для крыла бесконечного размаха. Мы уже видели, что И. с. эллиптического крыла вьфажается след. обр.: следовательно, коэфф. JV представляет собою увеличение И. с. над значением его, получающимся при эллиптическом распределении циркулящ1И. Оказывается, что для целей практики совершенно достаточно бывает брать для определения коэффициентов Ах,Аз, J-g только четыре члена тригонометрического ряда и удовлетворять этому ряду только в четырех точках; тогда мы будем иметь четыре ур-ия с четьфьмя неизвестными. Для удобства вычислений можно брать сечения полукрыла, соответствуюпще значениям В, 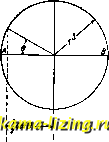
Фиг. 11. 1Ж ш ж Фиг. 12. равным 22,5°, 45°, 67,5° и 90°, отстоящим от середины крыла на расстоянии соответственно 0,924 [ ; 0,707 [ ; 0,383 и О (фиг, 12). В этом случае система уравнений будет иметь следующий вид: I. 0,383 ( 1+0,383) J:i-f 0,924 (3/ti-Ь0,383)3-Ь +0,924 (5*1+0,383) 5+0,383(7/ii-f-0,383)47= =0,383 (Jo)i; II. 0,707 (а<2+0,707) 1+0,707 (3/2+0,707) Л,--0,707 (5/2 + 0,707) Л-0,707 (7/2+0,707) .4= = 0,707 (Jo); III. 0,924 (/3+0,924) Ai-0,383 (3/*з +0,924) А.- 0,383(5/3+0,924) А5+0,924(7/*з+ 0,924) = 0,924 (Jo); rV. (/i, + l)i-(3/*, + l)3 + (5/*. + l)5--(7/*4 + l) Л = ( /0)4:. Т. о., для определения И. с. какого угодно крыла необходимо иметь характеристику профилей в рассматриваемых сечениях при бесконечном размахе. Характеристики для конечного размаха определяются опытным путем. Выше был уже изложен приближенный метод пересчета с конечного размаха на бесконечный. Этот метод, однахад, являющийся точным для эллиптич. крыла, не дает возможности более точно подсчитать характеристику бесконечного размаха для крыльев других форм. В аэродинамич. лабораториях обычно испытьшают крылья прямоугольные, поэтому в первую очередь необходимо уметь пересчитывать на бесконечный размах характеристики этих крыльев. Подставляя в формулу (17) значение площади крыльев S = lb, а также принимая во внимание уравнение (18), получим: А, , Су л А, (19) Кроме того, коэфф. N зависит от величины /*, таккак в ур-иях I, II, III и 1Y коэфф-ты Al, A3, А и А7 определяются через /*. На фиг. 13 даны величины -Л и JV в зависи-По этим графикам, если мости от -r-s известна характеристика профиля для бесконечного размаха, можно найти также характеристику прямоугольного крыла. Для решения обратной задачи на тех же графиках нанесен другой масштаб - для , где /S-угол абсцисс данно- Кривые пвпрвВот>1Ж прямоугадыюго iqibUu
2 3 4 Фиг. 13. наклона к оси характеристики го профиля прямоуголь-hcfro крыла. Таким же образом можно вывести поправочные коэффициенты для каких угодно крыльев. Однако, приближенно можно для нек-рых форм крыльев пользоваться следующими формулами. Трапецоидальное крыло (фиг. 14): для , равных от до Да = отношений Крыло с закруглен, концами (фиг. 15): 0,730 Да = Все вычисления по этим ф-лам производятся указанным выше способом, только при нахождении И. с. и скоса потока следует подставить вместо величины А ее новое соответствующее значение. Как уже было указано, по теории Треф-ца распределение циркуляции по размаху С-) Фиг. 14. Фиг. 15. можно представить в виде определенной кривой. Эта кривая выражается следующим уравнением: J = 2 (Al sin 0 + A3 sin 39 + + A5sin59+A7sin7e). (20) Когда коэфф-ты Ai, A3, As и A7 определены для соответствующих б вышеуказанным способом, то можно построить и эту кривую. при наличии подъемной силы крыло отклоняет набегающий на него поток на некоторый угол, а следовательно, и сзади крыла поток будет также скошен на определенный угол (фиг. 16). Этот скос потока за крылом вызывается как вихревой пеленой, так и присоединенньши вихрями. Так как стабилизатор обычно располагается
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||