может быть определен измерением напряжений в различных точках схемы по формуле:

тд,еУх2=т Lxzh-напряжение между точками Л и. В; со-угловая частота; Vi=i(o LI-;

отсюда = ~ (при этом контур II разомкнут И возбуждается лишь контур I).

Фиг. 4.

Фиг. 5.

Затем процесс измерения повторяется при разомкнутом контуре I и возбуждении контура II; в этом случае получается = Подробности см. Связь.

Лит.: см. Связь. В. Баженов.

ИНДУКТИВНОЕ СОПРОТИВЛЕНИЕ, сопротивление, к-рое получается у движущегося в жидкости тела при наличии циркуляции, обусловливающей по теореме Жуковского нек-рую подъемную силу от определенной системы вихрей, образовавшихся в жидкости при движении данного тела (см. Вихревая теория). Эти вихри образуются следующим образом.

Предположим, что нек-рое крылообразное тело движется в воздухе; у него сила сопротивления получается как за счет трения, так и за счет придания некоторой массе воздуха определенных скоростей. При наличии у этого крыла подъемной силы, т. е. силы, перпендикулярной к направлению движения потока, струя над крылом сужается, а под .крылом расширяется, за счет чего соответственно получаются ббльшие и меньшие скорости разных направлений; от этого по всему размаху крыла образуются вихри, составляющие общую вихревую пелену (фиг.1), к-рая, сходя с крыла, практически, вследствие вязкости воздуха, понемногу размывается.

В теории И. с.пользуются методом, часто применяемым в гидродинамике: предполагается, что крыло создало определенную систему вихрей и эти вихри выбывают определенное поле скоростей. Чтобы охватить математич. анализом действие вихрей на окружающую их жидкость, предполагается, что с задней кромки крыла сбегает множество элементарных вихрей с циркуляцией J, при чем, т. к., с точки зрения гидродинамики, всякий вихрь не может кончиться внезапно, то, в согласии с теорией подъемной силы крыла аэроплана, предполагается, что сбегающие с крыла вихри идут внутри крыла в виде нек-рых фиктивных, т. н. присоединенных вихрей с циркуляцией в каком-либо сечении крыла плоскостью, перпендикулярной размаху, равной сумме циркуляции элементарных вихрей, проходящих по одну сторону этой плоскости.

Фиг. 1.

Согласно вихревой теории, вихри вызывают в потоке некоторую добавочную скорость; последняя, слагаясь с относительной скоростью движения крыла, дает ту истинную скорость, с к-рой воздух подходит и отходит от крыла. В общем случае эта вызванная скорость не постоянна по размаху крыла, а будет зависеть от интенсивности расположения элементарных вихрей, составляющих сходящую с крыла вихревую пелену. В частном случае система вихрей будет состоять из концевых и присоединенных прямолинейных вихрей-это т. н. П-образ-ные вихри. В некоторых случаях практики для упрощения расчетов м. б. принята приближенно эта схема распределения вихрей.

Зная вызванные определенной системой вихрей скорости и составляя уравнение связи крыла с потоком, т. е. связь между ги-дродинамич. величинами, характеризующими поток, и величинами, характеризующими крыло данной формы, можно найти и необходимые характеристики каких угодно крыльев. Теория И. с. играет чрезвьгаайно большую роль в практике аэродинамич. расчета самолетов {(Ж. Аэродинамика, расчет самолета), т. к. она позволяет по продувкам индивидуальных крыльев находить характеристики любых сложных крыльев. Так, по характеристике моно-планных крыльев различных профилей можно найти характеристики сложных крыльев, скомбинированных из этих профилей и как угодно расположенных в крыле; такими крыльями будут конические крылья, крылья с различными установками профилей, т. н. скрученные крылья, бипланы, тендемы и т. д.

Рассмотрим влияние прямолинейного бесконечного шнура с циркуляцией J (фиг. 2) на какую-либо точку жидкости А и определим вызванную этим шнуром скорость в этой точке. Согласно сказанному в статье Вихревая теория (ТЭ,т. 3, ст. 776), бесконечно малый элемент шнура ds вызовет в точке А элементарную скорость

Так как г =

dv=--i-sivLtpds.

4 яг

rd(p

Vi. ds =

sin q> Sin <p sin* <p вызванная элементарная скорость J

dq), TO

Sin q}

Интегрируя в пределах углов от (р до tpi, получим полную скорость точки А от действия части вихря, заключенного между этими углами:

<Pi

v = 7 J sin pd?> = (cos??2-cos9Ji). (2)

4ял:

В случае бесконечного шнура?;2=О, <Pi=, и скорость

в случае полушнура, т. е. шнура, только одним концом простирающегося в бесконеч-

ность, а другим лежащего на перпендикуляре АВ, fp%=Q, gi = I и скорость

Рассмотрим скорость, вызванную вокруг крыла вихревой пеленой. Для этого будем полагать, что эта вихревая пелена аналогична бесконечному ряду П-образных вихрей (фиг. 3). Возьмем какое-либо сечение крыла плоскостью, перпендикулярной к раз-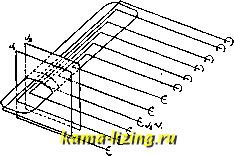

Фиг. 3.

маху и направленной по потоку, а также второе сечение, бесконечно близкое к первому. Обозначим щ-1ркуляции по контуру, охватьшающему крыло и находящемуся в проведенной плоскости, соответственно через Ji и Jg. Выберем прямоугольную систему координат т.о., чтобы ось X шла по размаху крыла, ось У-ПО направлению дви-Z жения крыла и ось Z-

перпендикулярно первым двум. Пусть на фиг. 4 кривая вех представляет собою закон распределения циркуляции по Ьл размаху. Обозначим абс-Фиг. 4. циссы положения вихрей

через X, а абсциссы точек крыла-через f. По ф-ле (4), скорость, вызванная элементом вихря с абсциссой х в точке А с абсциссой , будет:

dv = ~

dx х-§

Интегрируя это выражение по всему крылу, т. е. в пределах от - до Н- , получим скорость, вызванную рассмотренной системой вихрей в точке А:

4п S dx

dx x-S

Рассмотрим теперь действие на поток вокруг крыла одного П-образн. вихря (фиг. 5). По ф-ле (4) можно найти скорость, вызванную одним полушнуром:

= ~-

Эта скорость по размаху будет меняться по гиперболич.закону. Найдем среднюю по размаху величину этой вызванной скорости и назовем ее vp Т. к. концевые вихри, как показывает опыт, идут на нек-ром расстоянии от конца крыла, то обозначим раз-

мах крыла через I, рарстояние между центрами вихрей-через li и расстояние от центра вихря до конца крыла-через е; тогда

Величина средней скорости

Так как в нашей системе имеются два вихря, то вызванная каждым вихрем средняя скорость удваивается, и средняя скорость, вызванная двумя концевыми вихрями в точке А, лежащей на присоединенном вихре, выразится так:

l + e

-.---.---ч:г:

Фиг. 5.

Приближенно, на основании опыта, можно принять, что fi=M,05; тогда

И, следовательно, средняя скорость

Чтобы найти ур-ие связи крыла с потоком, воспользуемся теоремой Н. Е. Жуковского (см. Аэродинамика, т. 1, ст. 835), по к-рой подъемная сила через циркуляцию выражается след. обр.:

p = e.j.F.l. (7)

с другой стороны, эту подъемную силу можно выразить та1сже следующей ф-лой (см. Аэродинамика, т. 1, ст. 841, ф-ла 6):

Сравнивая эти две ф-лы, получаем:

j9miC,

подставляя же это выражение для J в ф-лу (6) и вводя обозначение А = , к-рое называется относительным размахом или удлинением крыла, найдем:

Наличие этой скорости, вызванной вихрями, обусловливает собой отклонение относительной скорости потока у крыла на определенный угол Да = . Этот угол назьшается скосом потока. Вследствие наличия скоса потока крыло в действительности встречает поток не под углом атаки а, а под углом а -Да (фиг. 6).

Подъемная сила крыла, движущегося со скоростью F, перпендикулярна скорости движения крыла. Это-та подъемная сила, с к-рой обыкновенно оперируют и к-рую находят при аэродинамич. испытаниях крыльев. Вследствие того, что направление потока скошено на угол Да, подъемная сила также откинута назад на угол Да. Если спроектировать ее на направление движения крыла, то получится некоторая сила Qi, направленная по скорости движения, т. е. некоторая сила лобового сопротивления, вызванная строением самого потока около

крыла и называемая индуктивным сопротивлением. Но при движении крыла от трения поверхности крыла о воздух и от различных побочных вихреобразо-ваний создается еще сила лобового сопротивления , зависящая исключительно от индивидуальных особенностей профиля крыла. Это сопротивление называется профильным сопротивлением; обозначим его через Qp. Индуктивное и профильное сопротивления создают то лобовое сопротивление, которое и наблюдается при испытаниях крыла. Т. о., полное лобовое сопротивление

Т.к. скос потока является величиной сравнительно небольшой и проекция подъемной силы на новое направление изменит ее очень мало, то приближенно принимают, что подъемная сила за счет скоса потока изменяется незначительно; большое же изменение ее происходит за счет изменения угла атаки.

Согласно фиг. 6, И. с. выражается следующим образом:

Qi = P Асе, а полное лобовое сопротивление

Подставив в эту ф-лу выралсения сопротивлений через коэфф-ты сопротивлений, будем иметь:

C-Q-S-V=Cy-Q-SV-Aa + Cp-Q-S-V, где Ср можно назвать коэфф-том профильного сопротивления. Деля все выражение на Q S - V, получим:

С=СуАа + Ср, (10)

или Ca. = Oj+Cp, где Cj--коэфф-т индуктивного сопротивления, выражающийся следующим образом:

С,= С.Да. (11)

Коэфф. профильного сопротивления, icak зависящий от индивидуальных особенностей профиля, не м. б. найден теоретич. путем; коэфф-т же И. с. зависит от угла скоса:

Подставляя сюда найденное значение для средней вызванной скорости, получим:

(12)

или, выражая угол скоса в градусах,

Да° = 57,3-

Т. О., коэфф. И. с. может быть представлен следующей ф-лой:

Это-ур-ие параболы, ось к-рой проходит через ось Ci- Эта парабола называется параболой индуктивного сопротивления. Обозначим через А; тогда

Ci=ACl. (14)

А является, следовательно, параметром па-

ПврабЬла имЗухтиб

Фиг. 7.

раболы И. с. и зависит только от относительного размаха Я. При увеличении Я ветви параболы будут приближаться к оси ординат-парабола будет делаться более раскрытой ; при А=оо, Jl=О-парабола обращается в ось ординат.

Так. обр., И. с. зависит от подъемной силы и от относительного размаха: при одной и той же подъемной силе, чем больше относительный размах, тем меньше И. с; при бесконечном размахе И. с. равно нулю и, следовательно, все лобовое сопротивление крыла сводится только к профильному сопротивлению. С другой стороны, при одном и том же относительном размахе И. с. меняется в зависимости от подъемной силы, и при нуле подъемной силы все лобовое сопротивле1ше сводится только к профильному сопротивлению, т. к. в этом случае И. с. равно нулю.

Поляра Лилиенталя дает характеристику данного крыла (см. Аэродишжша). На каком-либо угле атаки а отрезок АС, параллельный оси абсцисс, будет представлять собою лобовое сопротивление дан- Су ного крыла (фиг. 7). Для имеющегося у этого крыла а относительного размаха Я можно по ф-ле (13) построить параболу И. с; тогда отрезок АВ будет представлять собою И. с. этого крыла, соответствующее определенной подъемной силе. Отрезок ВС будет, следовательно, равен С, т. е. профильному сопротивлению. Т. о., при помощи приведенных ф-л можно решать основные задачи теории И. с, которые находят большое применение на практике.

Одной из главных задач является нахождение характеристики крыла одного относительного размаха по характеристике крыла другого относительного размаха, или нахождение характеристики биплана или вообще полиплана какого угодно размаха по характеристике моноплана. Т. к. аэродинамич. лаборатории обьгано дают характеристику монопланного крыла для относительного размаха, равного 5 или 6, то при аэродинамическом расчете самолета приходится находить характеристику крыла для того относительного размаха, который имеется на рассчитываемом самолете.

Исходя из теории П-образных вихрей в случае биплана или вообще полиплана, можно также найти все поле скоростей. Метод, данный для этого Бетцем, состоит в том, что путем последовательных приближений находят влияние одного крыла на другое при каком угодно расположении и величине крыльев; однако, он требует длительных вычислений, и поэтому мы приведем здесь лишь приближенную ф-лу для полипланов, данную проф. Прандтлем. Под коэфф-тами сопротивления полиплана мы будем подразумевать коэфф-ты суммарного действия планов, получающиеся по правилу смешения, т. е. коэфф-ты подъемной силы и лобового сопротивления полиплана будут:

s.+s,+ ... +s