зятся также взаимно перпендикулярными линиями. Главные направления вообще не совпадают с направлениями меридианов и параллелей, за исключением тех проекций, на к-рых меридианы и параллели пересекаются под прямыми углами.

Все существующие проекции по свойству изображения и по способу построенияпод-разделяются на различные виды. По свой- ству изображений проекции бывают: 1) конформные, или равноугольные (автогониче-ские), 2) эквивалентные, или равновеликие, иЗ) произвольные. На конформных проекциях сохраняется подобие очертаний контуров, но в разных местах проекций масштаб будет различный. Равные меледу собою кружки, взятые в разных точках земной поверхности, на проекции изобразятся таклсе крулс-ками, но радиусы их в разных местах проекции будут различные. В эквива.яент-н ы X проекциях частные масштабы по разным направлениям различны, но средняя величина масштаба во всех местах проекции постоянна, т. е. эти проекции сохраняют равенство площадей. Каждый кружок, находящийся на поверхности земли, изобразится на проекции равновеликим ему эллипсом (подобие фигур здесь не сохраняется). Произвольные проекции не сохраняют ни подобия контуров ни равенства площадей, но удобны для решения практических вопросов (простота построения). По способу построения проекции делятся на: 1) перспективные, 2) зенитальные, 3) цилиндрические, 4) конические, 5) поликонические, 6) многогранные, 7) условные. Те из перечисленных проекций, при которых контуры непосредственно проектируются на картинную плоскость, называются азимутальным и, так как в них каждая точка карты имеет тот же азимут относительно среднего меридиана, что и на земном сфероиде.

I. Перспективные проекции. В этих проекциях контуры земной поверхности изображаются так, как они представлялись бы в перспективе на картинной плоскости. Картинная плоскость располагается перпендикулярно к оптич. оси проекции,т. е.к линии, соединяющей точку зрения с центром земли. В перспективных проекциях изображаются очень большие части земной поверхности (целое полушарие), поэтому масштаб для них берут мелкий и землю принимают

за правильный шар с радиусом E=a(l- у),

где а-большая полуось, е-эксцентриситет земли. Перспективные проекции делятся на: 1) ортографические, когда точка зрения удалена от поверхности земли на бесконечное расстояние, 2) стереографически е-точка зрения лежит на поверхности земли, 3) центральны е- точка зрения в центре земли, 4) в н е ш-н и е-точка зрения вне земли, но на конечном расстоянии. Смотря по тому, пересекает ли оптич. ось проекции земную поверхность в полюсе, на экваторе или под промежуточной широтой, эти проекции бывают: п о-лярные, экваториальные и горизонт н ы е.

Ортографические проекции не сохраняют ни подобия фигур ни равенства

площадей; частные масштабы меняются от 1 (в центре карты) до О (у краев). В полярной ортографическ. проекции (фиг. 1) картинная плоскость совпадает с плоскостью экватора, меридианы на ней изображаются прямыми линиями, пересекающимися в центре карты под углами, равными разностям их долгот, а параллели-концентрич. кругами. В экваториальной проекции (фиг.. 2) картинная плоскость совпадает с плоскостью какого-нибудь меридиана; меридианы представляются эллипсами, имеющими общую ось, равную диаметру земли, а малые оси их равны 2EsinA, где Я-долгота данного меридиана; параллели же изображаются параллельными прямыми, отстоящими от центра проекции на величины R sin (р, где <р-широта данной параллели. В гордзонтцой проекции (фиг. 3) картинная плоскость проходит через центр земли параллельно горизонту любой данной точки; меридианы и параллели изображаются эллипсами, кроме меридиана цен-аль-ной точки, к-рый будет прямою линиею. Ор-тографич. проекции пригодны для изображения небольших частей земной поверхности; для целого же полушария они применяются в картах луны.

Стереографические проекции сохраняют подобие очертаний контуров. Частные масштабы в них меняются от (в центре) карты до 1 (у краев). В полярной проекции (фиг. 4) картинная плоскость лежит в плоскости экватора; меридианы в ней изо-бралсаются прямыми, пересекающимися в центре под углами, равными разностям их долгот, а параллели-концентрич. кругами. В экваториальной проекции (фиг. 5) картинная плоскость совпадает с плоскостью какого-либо меридиана; меридианы и параллели получаются в виде дуг неконцен-трич. кругов, за исключением среднего меридиана и экватора, к-рые представлены двумя взаимно перпендикулярными диаметрами. В горизонтной проекции (фиг. 6) картинная плоскость проходит через центр земли, параллельно горизонту данной точки; меридианы и параллели выражаются кругами. Стереографич. проекции применяются для изображения целых полушарий: восточного и западного или северного и южного; отдельные страны изображаются в них весьма редко. Они также применяются для графич. решения многих астрономич. задач.

Центральные проекции. Точка зрения помещается в центре земного шара, а картинная плоскость проводится касатель-ною к поверхности земли. Они не сохраняют ни подобия очертаний ни равенства площадей. Частные масштабы меняются от 1 (в центре проекции) до бесконечности (на краях), поэтому целого полушария изобразить в них нельзя. В полярной проекции (фиг. 7) картинная плоскость касательна к одному из полюсов; меридианы получаются в виде прямых, расходящихся из центра под углами, равными разностям их долгот; параллели же-в виде концентрич. кругов. В экваториальной проекции (фиг. 8) картинная плоскость касается какой-нибудь точки на экваторе; средний меридиан и экватор изобразятся двумя взаимно перпендикулярными прямыми линиями; все прочие меридиа-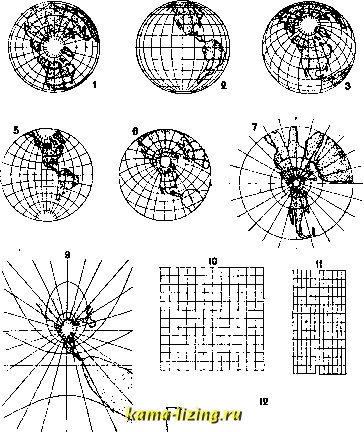

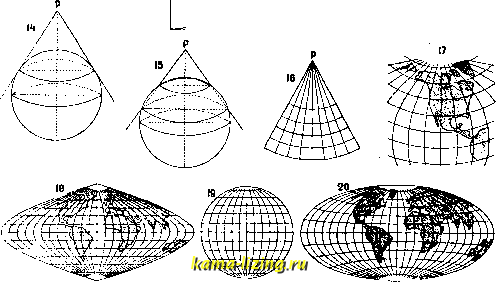ны-также прямыми, параллельными среднему и отстоящими от него на непрерывно возрастающих расстояниях; параллели будут иметь вид гипербол. В горизонтной проекции (фиг. 9) картин, плоскость касается данной точки под промежуточной широтой; меридианы получаются в виде прямых, расходящихся из полюса, но под разными углами; параллели с широтою >, чем90°-(где <Ро-широта точки касания), изобралсаются эллипсами; параллели с широтою 90°- щ- параболою, все же прочие - гиперболами, а экватор-прямою линиею. Центральные проекции применяются с успехом для изображения части небесной сферы, т. е. для звездных карт. Для изображения же всего неба его проектируют на 6 граней куба, описанного около шара и касающегося его в полюсах и четырех точках экватора.

Внешние проекции. Точка зрения в этих проекциях находится вне земного шара, но на определенном расстоянии. На внешних проекциях можно изобразить пространство большее, чем nojiapne. Меридианы и параллели на них вообще представляются кривыми второго порядка, в частности же на полярной проекции меридианы будут прямыми, расходящимися из полюса под равными углами, а параллели-в виде концентрическ. кругов. В проекции Лагира точка зрения удалена от поверхности земли на расстояние l = isin45° = 0,7071Е, где I-искомое расстояние, а R-радиус земли. В проекции Парана 1=0,5944R, у Длемса 1=:0,50000Б, у Кларка 1=0,367612. Внешние проекции не сохраняют ни подобия очертаний ни равенства площадей, но они дают меньшие искажения, чем остальные перспективные. Эти проекции применяются всего чаще в виде полярных.

2. Зенитальные проекции. В этих проекциях сферич. поверхность земли переносится на картинную плоскость, касательную к земле в данной точке, с таким расчетом, чтобы все точки, лежащие на шаре в равных расстояниях от точки касания, расположились на проекции по кругу с центром в точке касания. Наиболее употребительные из них- полярные, где меридианы изображаются прямыми, расходящимися из центра под равными углами, а параллели-концентрич. кругами. В полярной проекции Постеля радиус любой параллели е= R - gjj,где R-

радиус земли, а q>-широта данной параллели. В полярной проекции Ламберта радиус параллели с широтою д> будет

е=21г sin (45°-) .

3. Цилиндрические проекции. Для построения цилиндрич. проекций воображают цилиндр, касательный к земному сфероиду или секущий его. На поверхность этого цилиндра переносят по известным правилам меридианы и параллели, затем цилиндр разрезают по одной из образующих и развертывают на плоскость. Если ось цилиндра совпадает с осью вращения земли, то проекция называется прямою, если же ось цилиндра составляет с осью земли прямой угол, то проекция называется поперечною; наконец, если ось цилиндра наклонена к оси

вращения земли под произвольным углом, но не в 90°, то проекция называется к ос ою. Наиболее употребительны прямые цилиндрические проекции.

В к в а д р а-т н о й, или плоской, цилиндрической проекции (фиг. 10) цилиндр берется касательным к экватору. Все параллели и меридианы изображаются прямыми параллельными линиями, взаимно перпендикулярными, проведенными друг от друга на равных расстояниях, так что получаются квадраты. Стороны этих квадратов равны выпрямленным дугам экватора заданного числа градусов в заданном масштабе. Дуга 1° экватора, но Бесселю, равна 111 308,42 Jt. Масштаб т по всем меридианам и по экватору равен главному, т. е. т = 1. Частные масштабы п по разным параллелям раайтичны, т.е. w=sc у (где п-масштаб по параллели, а р-широта ее).

Прямоугольная цилиндрическая проекция (фиг. 11) строится на цилиндре, секущем землю по двум параллелям, равно отстоящим от экватора. Меридианы и параллели взаимно пересекаются под прямыми углами. При развертывании цилиндра получаются прямоугольники, большие стороны к-рых равны выпрямленным дугам меридиана в заданное число градусов, а малые стороны равны выпрямленным дугам параллелей сечения также в заданное число градусов. Называя частные масштабы по меридианам через т, а по параллелям-через п,

будем иметь: т = 1,п =

cosip

где -широ-

та параллели сечения, а 9?-широта данной параллели.

Изоцилиндрическая проекция (фиг. 12) строится на касательном к экватору цилиндре. Меридианы параллельны между собою и отстоят друг от друга на величины выпрямленных дуг экватора в заданное число градусов. Параллели перпендикулярны к меридианам, параллельны между собою, находятся друг от друга на разных расстояниях и отстоят от экватора на величины D, получаемые из формулы D=Esin?), где R-радиус земли, а 9?-широта-данной параллели. Называя масштаб по меридианам через т, по параллелям-через п и масштаб площадей-через М, будем иметь: т = cos 9?, W =sc 9?, Ж = cos 9? SC95 = 1, т. е. эта проекция равновеликая.

Проекция Меркатора (фиг. 13) сохраняет подобие очертаний фигур и строится на касательном к экватору цилиндре. Меридианы на ней изображаются в виде прямых, параллельных между собою и отстоящих друг от друга на величины выпрямленных дуг экватора в заданное число градусов; параллели же проводятся в виде прямых, перпендикулярных к меридианам и пересекающих их т. о., чтобы отношение дуг долгот каждой из параллелей на карте к прилегающим им дугам широт было одинаково с отношением соответствующих им величин на земле. Меридианные части, т.е. расстояния параллелей от экватора, удобно получать из таблиц возрастающих широт. Проекция Меркатора обладает весьма важным свойством для мореплавания: на ней локсодромия, т. е. кривая, прове-