Этот вывод построен в предположении невесомости самого вала. Если же учесть распределенную массу самого вала, то нужно вычислить момент инерции тела вала относительно оси вращения его (назовем его бо) и взять для расчета 0,33 0, считая уже всю массу сосредоточенной на конце вала.

3. Валы гибкие. В быстроходных мащинах (например паровые турбины) при ма-лейщем эксцентриситете масс на валу получаются громадные центробежные силы. При определении диаметра такого вала можно исходить из двух соверщенно различных положений: 1) можно определить прочные размеры вала, учитывая центробежные силы; в этом случае получаются солидные размеры всей конструкции, но расчет затрудняется вследствие того, что эксцентриситет массы на валу фактически остается неизвестным; 2) можно вычислить критич. скорость вала и затем, по возможности далеко от нее, назначить фактич. скорость; в этом случае конструкция получается легкой, и расчет вполне доступен, вал же называется гибким, так как он не дюжет сопротивляться указанной центробежной силе и легко гнется. Способность такого вала держаться против этой силы выясняется из фиг. 3. Здесь вверху показан гибкий вал в изогнутом положении, при чем осью вращения служит кривая линия АВ\ ц. т. сосредоточен в точке Мх эксцентрично по отнощению к оси вращения, е-эксцентриситет. Как видно, центробежная сила стремится еще больше изогнуть вал. Однако через полоборота точка Мх займет положение М, и центробежная сила будет теперь направлена уже вниз, вследствие чего вал будет выпрямляться.

Предположим, для общности, что деформация вала пойдет не по направлению эксцентриситета, а в сторону от него. Пусть SS (фиг. 4) будет направление недеформи-рованной геометрической оси вала, О А-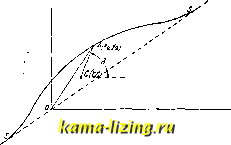

Фиг. 4.

стрела прогиба его в сечении, проходящем через центр тяжести, АС-эксцентриситет. Пусть координаты точки А будут а; и а точки С- и Г}. Раскладывая силы по координатным осям, получим:

т. Тсха=0- -Ь = 0. (10)

Назовем эксцентриситет АС через е. Тогда, как видно из фиг. 4,

= $ -Ь е cos d; = + б sin rf. (11) Если (О-угловая скорость вращения, а t- время, то d=(i)t. Тогда уравнения (10) получают следующий вид:

т-+ k(§ + ecos<x)t) = 0;

m + kin + esin ojt) = 0.

Введем теперь подстановку:

1 = 5-1-Ь cos < ri = & + bsino)t, (13)

где 5 и &-Новые переменные величины, а 6-константа. При такой подстановке мы в праве наложить на величину 6 какое угодно условие, чем и воспользуемся далее. После двойного дифференцирования ур-ий (13) и подстановки в (12) найдем:

-Ъ(0 COS (otj+ к (?-Ь5 cos (ot+e cos (j)t)=0;

m - bft)2 sin co -b ife (-t-bsin ft)i--e sin (at) =0; или после приведения подобных членов:

X \-kt, + (кЪ-\- ke-mbw ) cos (ot = 0;

m- -}-7c9-\- (kb -f ke-mbco) sin tot = 0.

(14)

Теперь наложим на величину 6 условие, чтобы

кЪ + ке - тЬо)2 = О,

откуда

(15)

тш - k Тогда из уравнения (14)

ш{-]-к==0;

m-f + k=0. Из (15) видно, что при

Ь обращается в бесконечность, следовательно на основании (13) и (11) заключаем, что координаты точки А обращаются в бесконечность, т.е. вал разрушается. Напротив, при

(16)

(17)

величина Ь имеет конкретное конечное значение. При очень большом значении (о величина Ъ приближается к нулю. Тогда ив (13): =t, и г]=д-. Ур-ия (16) характеризуют колебательные движения вала, которые при большом (1) по сравнению с / - оказываются за пределами критическ. скоростей. Таким образом при расчете гибкого вала следует: 1) рассчитать его на передаваемый крутящий момент; 2) проверить по ф-ле (17), для чего нужно вычислить величины ы, к я т [см. формулы (7) и 8)].

4. Веретена. В. веретен отличается той особенностью, что, по мере наматывания на катущку пряжи, масса системы веретена все время изменяется, а вместе с тем изменяется также и критич. число. Именно, с увеличением намотки критическ. число понижается.

Экспериментальное исследование В. ватерных веретен (хлопковых), опорных и подвесных, проведено в Кабинете прикладной механики Московского текстильного ин-та на специально построенной машине при помощи быстроходного вибрографа (см.).

Из этих опытов найдено: 1) веретено опорное вибрирует сильнее, чем подвесное; 2) у подвесных веретен расстояние между опорным седлом втулки и средним сечением блочка резко влияет на вибрацию: чем это расстояние больше, тем больше В. веретена;

3) амплитуда В. стандартного веретена, измеренная по верхнему концу шпинделя, в неблагоприятных случаях превосходит 2 мм;

4) В. данного веретена, при данном количестве намотанной пряжи и данном числе оборотов, носит устойчивый характер; 5) способ посадки шпули на веретено (плотная посадка нижней частью в чашечку или верхней частью на шпиндель, зазоры и т. п.) резко влияет на В. веретена; 6) натяжение шнура на вибрацию опорного веретена не влияет. Что касается подвесных веретен, то натяжение отражается на вибрации тем сильнее, чем больше расстояние, указанное в п. 2. См. Тахометр вибрационный. Осциллограф, Сейсмограф.

Лит.: Тимошенко С. П., Курс сопротивления материалов, гл. XIX, 9 изд., Киев, 1916; R а у-1 е 1 g h. The Theory of Sound, L., 1877-78; Morrow J., On the Lateral Vibration of Loaded and Unloaded Bars, PhiIos. Mag. , L., 1996, v. 2, p. 354; Hort W., Technische Schwingungslehre, В., 1922; S t о d 0 1 a A., Die Dampfturblnen, 4 Aufl., p. 293, В., 1910; L о г e n z H., Dynamik d. Kurbelgetriebe, Leipzig, 1901; Frahm H., Z. d. VDI , 1902, p. 779; Lorenz H., Kritische Drehzahlen rasch-umlaufender Wellen, Z. d. VDI , 1919, B. 63, p. 240; G ii m b e 1 L., Neue kritische Wellengeschwindig-keit bel mit Biegung verbundenen Schwingungep von Wellen, Dinglers polytechnisches Journab, Berlin. 1918, p. 71; Prandtl L., Beitrage zur Frage d. kritischen Drehzahlen, Dinglers polytechn. Journal*, В., 1918, p. 179; Foppl O., Kritische Schwingun-gen von schnellumlaufenden Rotoren, Ztschr. fur d. gesamte Turbinenwesen , Munchen - Berlin, 1918, Jg. 15, p. 157. A. Малышев.

В. судов. Упругие колебания корпуса судна, вызываемые различными силами периодического характера, благодаря большой частоте (редко ниже 100 пер/м.), уже при сравнительно небольшой амплитуде (несколько мм) отражаются неблагоприятно и на людях и на приборах, находящихся на судне. Они способны также порождать в корпусе судна явления усталости металла (см.). Местная В., в к-рой участвуют лишь отдельные части судна, м. б. устраняема в построенном судне дополнительным усилением корпуса в районе В. В общей В. судна весь его корпус участвует как один упругий брус, и у построенного уже судна она не м. б. устранена путем дополнительных усилений корпуса. Мерами к ее устранению являются: уничтожение усилий, вызывающих В., и надлежащий выбор периода этих усилий, если их нельзя уничтожить. Главнейшие усилия, вызывающие общую вибрацию судна: а) неуравновешенные силы инерции частей машины с прямолинейно возвратным движением; б) силы инерции неуравновешенных частей машины; в) неравномерность вращающего момента главной машины; г) неравномерность осевого давления гребных винтов; д) удары струй, отбрасываемых лопастями гребных винтов. Период этих усилий либо

совпадает с периодом г одного оборота машины [см. (б)] либо составляет от него простую долю вида , где п-целое число, В

случае (д) п-обычно число лопастей. Эти усилия вообще невелики и при статическом действии неспособны вызвать заметную деформацию судна. В. судна становится поэтому заметной лишь в условиях резонанса, когда период возмущающей силы совпадает с одним из периодов г-лавных свободных колебаний судна. Для уничтожения вибраций судна часто бывает достаточно изменить период возмущающей силы на 10-15%. Такое изменение числа оборотов главной машины является наиболее действительным средством к устранению В. у построенного уже судна и достигается переменою гребного винта. При постройке судов рекомендуется проектировать нормальное число оборотов либо на 10-15% меньше либо на 40-50% больше критического. Если период возмущающих усилий машины может совпасть с одним из периодов главных свободных колебаний судна, то все такие усилия должны быть тщательно уравновешены при проектировании машины (см. Уравновешение поршневых двигателей).

Главные свободные колебания судна-гармонические колебания, из которых слагается его колебание по инерции при отсутствии возмущающих сил; они обладают свойством затухаемости; периоды и формы их зависят от жесткости и массы судна и закона их распределения вдоль него. Основные свободные колебания судна: 1) поперечные: а) вертикальные, б) горизонтальные; 2) крутильные и 3) продольные. Каждому роду колебаний соответствуют свои формы и периоды главных свободных колебаний. Продольные колебания наблюдаются всего реже.

Из поперечных колебаний чаще всего наблюдаются вертикальные колебания. В основном тоне их пучности располагаются у концов судна и возле середины его. Две узловые точки получаются приблизительно (фиг. 5) на расстоянии длины судна от каждо-

------ .. го из его концов.

~ Фиг. 6 изображает общий характер упругой линии судна, соответствующей второму тону вертикальных колебаний; в ней имеются 3 узловых точки. В упругой линии третье- - ----го тона узловых точек - 4 (фиг. 7). Фиг. 7. За дифференциальное уравнение упругих поперечных колебаний судна обычно принимают:

Фиг. 5.

Фиг. 6.

где Е-модуль Юнга; I-момент инерции площади поперечного сечения продольных связей судна относительно его нейтральной оси; g-масса судна, приходящаяся на единицу его длины; v-вертикальное перемещение судна в сечении, находящемся на

расстоянии г от его левого конца; t-время. Граничные условия: = О и = О на обоих концах судна. Условия сопряже-

ния: V и непрерывны на всем протяжении судна; если масса судна распределена вдоль его оси (не сосредоточена в его отдельных сечениях), то, кроме того, EI и

также непрерывны.

Горизонтальные поперечные свободные колебания судна вполне аналогичны вертикальным. В их дифференциальном уравнении величина / - момент инерции, взятый не относительно горизонтальной, как у колебаний вертикальных, а относительно вертикальной оси.

При крутильных колебаниях сечения судна поворачиваются вокруг его продольной оси. Крутильное колебание основного тона (фиг. 8) имеет одну узловую точку, колеба-

Z ние второго тона-

------два узла; колебание третьего тона- три узла и т. д. (фиг. 9 и 10). За дифференциальное уравнение крутильных колебаний судна принимают:

где б-угол поворота поперечного сечения судна, лежащего на расстоянии z от его левого конца, и С-жесткость судна -----

при кручении, которую можно находить по Бредту

[12]; г-полярный момент инерции массы судна, приходящейся на единицу его длины, взятый относительно оси кручения.

Граничные условия: О на обоих концах судна. Если вся масса судна распределена вдоль его (не. сосредоточена лищь в его отдельных сечениях), то условия сопряжения: б и 1 непрерывны на всей длине судна.

Продольные колебания судна по форме сходны с крутильными. Их дифференциальное уравнение:

где го-осевое перемещение сечения, находящегося на расстоянии z от его левого конца; F-пло--у щадь поперечного

сечения продольн. Фиг. 10. связей в нем. Гра-

ничные условия и условия сопряжения аналогичны таковым при крутильных колебаниях. Уравнения (1) и (3) поддаются обычно лишь численному приближенному решению. Для определения периодов и форм главных свободных колебаний судна существуют следующие методы: 1) Релея (Rayleigh) [з *]; 2) Ри-ца (W. Rietz) [ 3) метод последовательных приближений [ 8- 4) метод Бьерено-Коха (Biereno-Koch) [ ]. Для на-

хождения вынужденных колебаний судна под действием заданной возмущающей силы можно воспользоваться методом Адамс-Штёрмера, приложение которого к этой задаче было дано акад. А. Н. Крыловым ].

Отмеченные методы дают достаточные средства для преодоления тех аналитическ. трудностей, которые связаны с нахождением свободных и вынужденных колебаний судна. В менее благоприятных условиях находится вопрос об определении тех величин, к-рые входят в ур-ия (1)-(3) в качестве коэфф-тов. Здесь не выяснено: 1) чему в точности следует считать равным модуль Юнга; 2) все ли продольные связи корпуса в равной мере м. б. зачитываемы в то его сечение, которое сопротивляется изгибу, сжатию и кручению; 3) вся ли нагрузка судна должна в равной мере зачитываться при определении величин qui, особенно в отношении грузов жидких и сыпучих; 4) какие погрешности проистекают от применения к судну (не-призматич. брусу) основных формул, выведенных для призматич. брусьев. Это особенно относится к нахождению форм и периодов высших тонов, на которые все эти погрешности оказывают обычно более сильное влияние. Для удовлетворительного решения этих вопросов необходима пока еще отсутствующая систематизация планомерно поставленных опытов. При нахонедении форм поперечных колебаний высших тонов следует также дополнять ур-ие (1) членами, учитывающими влияние прогиба от сдвигов, а также моментов сил инерции от движения массы, сосредоточенной в каждом сечении судна.

Для грубого определения периода вертикальных колебаний основного тона иногда пользуются эмпирической формулой Шлика:

где Т-период колебания судна в ск.; I- момент инерции площади поперёчн. сечения миделя в ж*; Р--вес судна в т; L-длина судна в м; С-коэфф., равный, по Шлику:

Для очень острых судов (миноносцы). . 3 450 ООО

пассажирских .........3150 ООО

грузовых судов полных очертаний . 2 800 ООО

О записи вибраций см. Паллографы.

Лит.: *) Lorenz Н., Tectrn. Elastlzitatslehre, p. 98, Munchen, 1913; ) В г e d t R., Krlt. Bemer-kungen 7ur Drehungselastizitat, Z. d. VDI , 1896, B. 40, p. 813; ) T о b i n A., Method ol Determining the Natural Ship Vibrations, Trans. Inst, ol Naval Architects , L., 1922;. *) P a V 1 e П к 0 G. E., A Method of Calculating Ship Vibrations, Engineer-ing , London, 1926, v. 121, p. 748; *) Красноперой е.. Применение метода Рица к исследованию свободных колебаний балок, Изв. Петроградского политехническ. института . П., 1916, т. 25, вып. 1-2; ) Сушенков Б. Л., О вычислении собственных колебаний непризматич. стержней, Ежегодник Союза морских инженеров , П., 1916, т. 1, ) Т и м о ш е н-к о с. П., Теория упругости, ч. II, § 42, СПБ, 1916; ) Philosophical Magazine*, L., 1905-1906; ) Jahr-buch d. Schiffbautechniscben Gesellschaft , В., 1901, В. 2; ) В 1 e г e n о, Proceedings of the I International Congress for Applied Mechanics*, Delft, 1924; ) Крылов A. П., О расчете вибраций корабля, производимых работой его машины, Ежегодник Союза морских инженеров . П., 1917, т. 2; ) Крылов А. Н., О вычислении вибраций корабля, производимых работой его машины, Изв. Российской акад. наук . П., 1918, т. 12, ч. I, стр. 915; Н. Johows Hilfsbuch f. d. Schiffbau, p. 666-681, 4 Aufl., ВегИп, 1920; Hort W., Technische Schwingungslehre, В., 1922; Сушенков Б., К вопросу о вычисл. своб. колебаний судна, Изв. С.-Петербургского политехи, ин-та , СПБ, 1914, т. 21, в. 2, стр.. 575. П. Панкович.