область применения виадуков с крупньши пролетами удерживается за железными В.

В качестве В. могут быть применены и железные висячие мосты, нередко дающие очень крупную экономию стоимости для больших пролетов.

Лит.: Передерни Г. П., Курс мостов, ч. I, 3 издание, М. -Л.. 1927, ч. II, отд. I-Каменные мосты. Л., 1925; Тимонов В. Е., Виадук Гараби, СПБ, 1884; Передерни Г. П., Каменный виадук пролетом в свету 50 метров, СПБ, 1908; Gay С, Fonts en maconnerie, Paris, 1924; S ё-j о u г n 6 P., Grandes voutes, Paris, 1913-1916; N о r d 1 i n g W., Blemoire sur les piles en char-pente m6tallique des grands viaducs. P., 1869; P о u-t h i e r E., Notice sur le viaduc de Mussy, Ann. des ponts et cli. . P., 1901, v. 1, p. 235; F r б h 1 i с h H., Der Umbau des Viaduc du Day* auf d. Linie Lausanne-Vallorbe der S. B. В., Schweiz. Bauztg. , Zurich, 1927, B. 89, J ; Sejourne P., Construction des ponts du Castelet, de Lavaur etc., Ann. des ponts et ch. , Paris, 1886, v. 2, p. 409; В о i s-n i e r, Le pont de Sidi Rached. Ann. des ponts et ch. , Paris, 1912, v. 3, p. 473; P i car d E., Notice sur la construction du pont de Montanges, Ann. des ponts et ch. , P., 1911, v. 4, p. 101; Stiider H., Steinerne Briicken d. Rhatischen Bahn, Berlin, 1926. о железобетонных виадуках: M6rsch E., Die Gmiindertobel-Brucke bel Teufen im Kanton Appen-zell, Ziirich, 1909; Foundations for the Tunkhannock Viaduct, Engineering Record*, N. Y.. 1913, p. 484. Статьи о виадуках: R i 11 e г M., Die Hundwilerto-belbriicke im Kanton Appenzell A.-Rh., Schweiz. Bauztg.o, 1926, B, 87, 13, p. 178; Buhler A., Der Umbau des Grandfey-Viaduktes der Schweiz. Bundesbahnen, Beton und Eisen , 1927, H. 19-22. По вопросу об усилении чугунных и жел. мостов железобетоном: Caufourier Р., Le renforce-ment au moyen de beton du pont metallique de Pulaski (Etats-Unis), GC , 1924, t. 85, 8, p. 175. O железных виадуках: Eiffel G., M6moire prsent6 к Iappul du projet definitif du viaduc de Garabit, P., 1889; V 1 r a r d M., Note sur la construction du viaduc des Fades, Ann. des ponts et ch. . P., 1903, v. 3, 1910, v. 1, p. 20; Dumas A., Achevement du viaduc des Fades, GC , P., 1909, t. 55, p. 81; Volontat et Th6ry, Notes sur la constructiondu viaduc du Viaur, Ann. des ponts et ch. , p., 1898, v. 1, p. 215, v. 2, p. 329, 1899, v. 1, p. 57, v. 4, p. 79, 1901, v. 3, p. 244; Martin H., Le viaduc du Viaur sur la ligne de Carmaux a Rodez, GC , 1903, t. 43, p. 1; В о d i n G., Le viaduc de IAssopos (Gr6ce), GC , 1909, t. 55, p. 289; Ст. об арочном виадуке: Caufourier P., Pont en arc de 195 metres de portee sur le Niagara, GC , 1925, t. 87, 22, p. 461; D i e t z W., Die Kaiser Wilhelm-Brucke iiber die Wupper bel Miingsten, В., 1904. H. Шошин.

ВИБРАТОР, В телефонной технике, прибор, включаемый в цепь генератора вызывного тока для контроля прохождения вызова. Устроен по принципу звонка перемен, тока, но вместо ударника имеет пластинку, колебания которой и служат сигналом.

ВИБРАТОР ГЕРЦА состоит из прямолинейного проводника с искровым промежуг-ком по. середине и двумя шарами по концам. Такой В. был впервые применен Г. Герцем в качестве излучателя электромагнитных волн и теория излучения этого вибратора дана им же. См. Диполь электрический.

ВИБРАТОР НАППА, установка для компенсирования сдвига фаз у асинхронных двигателей. В. К. состоит из трех машин постоянного тока, соединенных, как показано на схеме (фиг. 1), где S и. В-статор и ротор асинхронного двигателя, С-пусковой реостат, К-якоря упомянутых машин, М-обмотки возбуждения, питаемые постоянным током от постороннего источника. Ток ротора /а частоты скольжения (малой частоты jfg), проходя по якорям вибратора (компенсатора), находящимся в постоянном магнитном поле, образует вращающий момент, все время изменяющий свое напра-

вление в такт с пульсациями питающего тока J2, вследствие чего якоря начинают вращаться то в одну, то в другую сторону (отсюда название вибратор ). Вследствие таких маятникообразных качаний якорей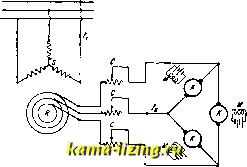

Фиг. 1.

в них индуктируется противодействующая эдс с частотой, равной частоте питающего тока. Так как все три якоря не совершают никакой работы на валу, то произведение Ез-12-со8 9?з=0. Здесь 3- сдвиг фаз между эдс Е и силой тока Jg. Поэтому каждый из якорей потребляет почти только реактивный ток (cos s = 0). Индуктирующаяся при движении в постоянном магнитном поле в каждом якоре вибратора эдс Е, опережает по фазе питающий ток. Действительно, если М-момент вращения, образуемый взаимодействием постоянного магнитного потока Ф с переменным током li, и D- момент инерции якоря, то, по уравнению моментов количества движения M-dt~B-d<t), где а>-угловая (механическая) скорость якоря.

т. к. л/=/Ci/jjSintOa, а а>=-Ал-вз,

ki-Ii sin o).J dt =-Jc2-Bdea,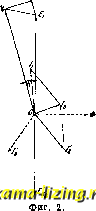

ki =

2tc-9,81 a

Отсюда

-e, =

sin o)J dt

где бз-мгновенное значение эдс Eg. Т.о. видно, что противодействующая эдс опережает по фазе силу тока, питающего вибратор. По отношению к напряжению на кольцах ротора асинхронного двигателя, рассматриваемый ток будет опережающим.

Вибратор Каппа действует как некоторая емкость, включенная в цепь ротора; величина ее равна

п 2 п / a\2 4ii-D-9,81

Благодаря получившемуся от действия вибратора опережению ток ротора будет намагничивать магнитную систему двигателя, вследствие чего сдвиг фазы силы тока li в статоре, по отношению к напряжению Т\, уменьшится и может стать отрицательным (фиг. 2). На диаграмме пунктиром cffs9 показано положе-

гов т SSO гт f£fipiw

{еа вибратора

Фиг. 3.

ние вектора силы тока в роторе li (приведенного к числу витков статора) в обыкновенном некомпенсированном двигателе.

Компенсирующее действие вибратора зависит от величины роторного тока. Поэтому при слабых нагрузках (небольших скольжениях) оно невелико. При скольжениях выше нормальн. вибратор не успевает работать в такт с изменениями тока ротора. Вследствие этого для недогруженных двигателей, а также и для двигателей, работающих с большим скольжением, В. К. уже не может быть применен. На фиг. 3 и4представлены кривые cos ц>, кпд щ и скольжения 8 трехфазного мотора 420 kW, 482 оборотов, 50 периодов в зависимости от нагрузки, без вибратора и с вибратором. Компенсирование сдвига фаз, производимое со стороны ротора асинхронных двигателей, имеет то преимущество, что оно совершается при ча-

cosip

Фиг. 4.

стоте скольжения, которое для больших двигателей не выше 2%. При этом реактив, мощность, которая развивается различного рода компенсаторами вообще и вибратором Каппа в частности, будучи пропорциональна частоте, составляет также ок. 2% от реактивной мощности, поступающей через статор и идущей на создание переменного магнитного поля. Вследствие этого размеры В. К. получаются относительно небольшие. В. К. работает без искрения, так как то время, когда сила тока достигает максимального значения, скорость движения якоря равна нулю, так что среднее значение реактивного напряжения в коммутирующихся секциях очень невелико.

Лит.: Шенфер К. И., Коллекторные двигатели переменного тока, М., 1922; Walker М., The Control of the Speed a. Power Factor of Induction Motors, London, 1924. E. Нитусов.

ВИБРАЦИИ, колебания упругого тела. Если вывести упругое тело из состояния равновесия и вызвать упругую деформацию f, то тело будет напряжено; если его вновь предоставить самому себе, то потенциальная энергия сил упругости поведет тело назад к состоянию равновесия. Этому обратному движению будет сопротивляться инерция массы тела, при чем движение будет тормозиться, и масса, поглощая потенциальную энергию деформированного тела, приобретает кинетич. энергию движения. Когда тело придет в положение равновесия, ки-

нетич. энергия возрастет до полного значения потенциальной, и сила инерции поведет тело от положения равновесия в противоположную сторону до тех пор, пока не вызовет. деформацию /. В этот момент кинетич. энергия вся будет израсходована, но зато напряженное тело будет иметь полный запас потенциальной энергии. Затем последует движение в обратном направлении, и т. д. Если бы никаких сопротивлений не было (трение, сопротивление среды и другие), то получилось бы вечное движение с постоянной амплитудой. В действительности эти колебания угасают довольно быстро. Когда сопротивления малы и ими можно пренебречь, вибрация является функцией двух сил-упругости и инерции. По Далам-беру (d Alarabert)

Р+И=0, (1)

где Р-сила эквивалентная силам упругости, а И-сила эквивалентная силам инерции.

Всякая деталь машины и всякое целое сооружение, простое или сложное, под действием толчка дает свою свободную, или собственную, В., период которой определяется ур-нием (1). Т. о. период В. зависит от параметров упругости (размеры соорунсения, способы закрепления опор, моменты инерции, модули упругости) и параметров инерции (массы, ускорения). Возбудителями В. могут быть все станки и машины, у которых малейшая неравномерность хода оказывается достаточной для порождения В. в деталях самой машины (в колесах, на валу, в станине, потолочных балках, колоннах, стенах здания и т. д.). При этом каждый толчок в машине возбуждает В. сразу во всех названных деталях и сооружениях. Под действием сопротивлений вызванная В. будет угасать, но если возбуждающие толчки по своему ритму совпадают с ритмом собственных В. сооружения или одной его детали, то получается накопление деформации, или так называемый резонанс. Критическим числом возбуждающих толчков называют то число их, которое совпадает с числом собственных колебаний тела в единицу времени. Каждой детали сооружения соответствует определенное критическое число.

В виду тбго, что абсолютно упругих тел нет, часть энергии возбуждающих толчков идет на преодоление необратимых молекулярных сопротивлений, чем и объясняется так наз. упругий гистерезис. Чем меньше этот гистерезис у тела, тем опаснее для него возникновение В., так как ббльшая часть возбу-недающего импульса пойдет на .изменение упругого состояния (количества движения), при чем неизбежно накопление деформации. Наоборот, чем больше упругий гистерезис какого-либо тела, тем, при прочих фщ, i равных условиях, менее опасны возникающие в нем вибрации, так как последние сопровождаются меньшими упругими деформациями. Вследствие этого у большинства те.д нри наступлении резонанса амплитуда вибраций возрастает только до некоторого определенного предела..

1. Балки. Пусть брус АВ (фиг. 1) подвергается растягивающему действию груза G, при чем весом самого бруса можно пренебречь. Статическая деформация = ~~

(где I-длина бруса, F-площадь поперечного сечения его и Е-модуль упругости первого рода) не влияет на В. Под действием какого-то другого усилия Р брус получит

временную динамич. деформацию А =

которая, вследствие кратковременности действия Р, пойдет на убыль, при чем разовьется сила инерции массы груза G. По ф-ле (1)

G dX , EF

Я =0,

откуда

1 + Ш = О,

EFg G-l

Из дифференциального уравнения (2) определяется период одного полного колебания бруса

T = i- . (4)

Подстановкой из ур-ия (3) величины к в ур-ие (4) находим Т, выраженное в секундах. Число собственных колебаний бруса в минуту будет

п = 4- (5)

При таком числе возбуждений в минуту брус попадает в состояние резонанса. Т. о. критическое число для бруса

30 / E-Fi к у G-1

При изгибе балки число ее собственных колебаний в минуту определяется аналогично. Разберем два основных случая.

Случай 1. Балка защемлена одним концом, а на другом конце нагружена весом G. Собственным весом балки пренебрегаем. Динамич. прогиб f будет вызываться кратковременной дополнительной нагрузкой Р. Сила упругости, соответствующая динамич.

деформации, будет р=М1д где I-длина

балки, а EI-ее жесткость. Сила же инерции будет выражена так (для груза G):

Я = - Т. о. из уравнения (1) найдем:

а dt г откуда получается дифференциальное ур-ие

Ж1 + =0, (6)

при чем

- GI*

Так как ур-ие (6) аналогично ур-ию (2), то пользуемся решением его (4) и получаем:

откуда критическое число в минуту

=jAip. (7)

Случай 2. Балка свободно лежит на двух опорах и посредине нагружена грузом 6г. Этот случай отличается от предыдущего

г. Э. т. III.

ТОЛЬКО числовым коэфф-том в выражении силы упругости, соответствующей динамической деформации. Именно в этом случае

На этом основании сразу получаем критическое число

iBEIg

при определении колебаний балок с учетом собственного веса их часто пользуются приближенными коэфф-тами, при помощи которых распределенный груз балки заменяется эквивалентным ему сосредоточенным грузом. Так, для балки постоянного сечения, защемленной одним концом, вес ее Q можно заменить сосредоточенным на свободном конце грузом, равным 0,25 Q, а для балки, свободно лежащей на двух опорах, распределенный вес ее можно заменить сосредоточенным в середине пролета грузом, равным 0,5 . Затем задача будет решаться так же, как изложено выше, по формулам (7) и (8).

2. Валы жесткие. Для длинных пароходных валов, а также трансмиссионных валов вычисление периода собственных колебаний м. б. сделано по следующему плану. Пусть (фиг. 2) дан вал АВ, у к-рого на конце

имеется некоторая шайба С (шкив, муфта, зубчатое колесо и пр.). Элемент этой шайбы dm, двигаясь по дуге круга ds радиуса q, подвергается тангенциальной силе инерции (дифференциальной)

Дифференциальный момент этой силы относительно оси вращения

dMu = dm, q

откуда Ми dt -момент инерции тела шайбы относительно оси вращения. В то же время момент упругих сопротивлений вала скручиванию будет

Так как Ми -f Ж = О,

?.+ ¥- = 0;

- т

1о - полярный момент инерции сечения вала относительно оси вращения, G-модуль упругости 2-го рода, I-длина вала. По аналогии С вышеизложенным определим критическое число:

отсюда

при чем

зо / VG

(9) 22